* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Packet 1 for Unit 6 M2G
Multilateration wikipedia , lookup
Golden ratio wikipedia , lookup
History of geometry wikipedia , lookup
Line (geometry) wikipedia , lookup
Perceived visual angle wikipedia , lookup
History of trigonometry wikipedia , lookup
Reuleaux triangle wikipedia , lookup
Trigonometric functions wikipedia , lookup
Rational trigonometry wikipedia , lookup
Euclidean geometry wikipedia , lookup
Incircle and excircles of a triangle wikipedia , lookup
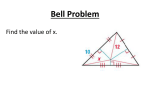
M2 GEOMETRY PACKET 1 FOR UNIT 6 – SECTIONS 5-1, 5-2, 5-3 SEGMENTS IN A TRIANGLE ASSIGNMENT SHEET FOR PACKET 1 OF UNIT 6 This packet includes sections 5-1, 5-2, and 5-3 from our textbook and the review for those sections. Date Due Number Assignment Topics 6A p. 329 – 331 # 9, 12, 14, 17 – 20 all, 34, 35 6B p. 330 – 331 # 23, 25 – 30 all, 32, 33 6C p. 340 – 341 # 5 – 10 all, 20 – 23 all 6D p. 341 # 24, 25, 27 – 30 all 6E p. 348 – 349 # 8, 14, 15, 18, 23, 29, 31, 35 5-1 Bisectors of Triangles Vocabulary: perpendicular bisector, circumcenter Investigate properties of perpendicular bisector and circumcenter Use algebra to solve problems involving perpendicular bisector and circumcenter 5-1 Bisectors of Triangles Vocabulary: angle bisector, incenter Use algebra to solve problems involving angle bisector and incenter 5-2 Medians and Altitudes of Triangles Vocabulary: median, centroid Use algebra to solve problems involving median and centroid 5-2 Medians and Altitudes of Triangles Vocabulary: altitude, orthocenter Use algebra to solve problems involving altitude and orthocenter 5-3 Inequalities in One Triangle Use the Exterior Angle Inequality to compare measures of angles formed by a triangle Use the side lengths of a triangle to order the measure of its angles Use the measures of the angles in a triangle to order the lengths of its sides Quiz on 5-1, 5-2, 5-3 1 M2 GEOMETRY PACKET 1 FOR UNIT 6 – SECTIONS 5-1, 5-2, 5-3 SEGMENTS IN A TRIANGLE Investigation – Perpendicular Bisectors of a Triangle Part 1: The Circumcenter Use Geogebra (www.geogebra.org) to answer the following questions. 1. Use the Polygon Tool to draw ∆𝐴𝐵𝐶. Click on point A to close the triangle. Polygon Tool 2. Select Perpendicular Bisector (see image at right). Click on each side of the triangle to draw its perpendicular bisector. 3. Each line is a perpendicular bisector of one side of the triangle. What does that mean? 4. Use the arrow tool to drag point A, B, or C. Notice that all three perpendicular bisectors always intersect at a single point. This point is called the circumcenter of the triangle. We’ll investigate what this means in Part 2. 5. Use the Point Tool to form the circumcenter, point D. 6. Last semester, we found the following properties of perpendicular bisectors: Perpendicular Bisector Theorem If a point is on the perpendicular bisector of a segment, then it is equidistant from the endpoints of the segment. Converse of Perpendicular Bisector Theorem If a point is equidistant from the endpoints of a segment, then it is on the perpendicular bisector of the segment. What does this mean about the distances DA, DB, and DC? 2 M2 GEOMETRY PACKET 1 FOR UNIT 6 – SECTIONS 5-1, 5-2, 5-3 SEGMENTS IN A TRIANGLE Part 2: Properties of the Circumcenter Because DA = DB = DC when D is the circumcenter of ∆𝐴𝐵𝐶, D forms the center of a circle that passes through A, B, and C. Circumcenter Theorem The perpendicular bisectors of the sides of a triangle intersect at a point called the circumcenter that is equidistant from the vertices of the triangle. 7. Suppose P is the circumcenter of △EMK in the diagram at right. a. By the Circumcenter Theorem, PK = ______ = ______. b. Name any segments that have the same length as the given segment below: ̅̅̅̅̅ (i) 𝑀𝑌 ̅̅̅̅̅̅ (ii) 𝑀𝑁 ̅̅̅̅ (iii) 𝐸𝑅 Open the Geogebra applet at https://www.geogebra.org/m/XnzAPaT3. In the applet, you should see a triangle with its perpendicular bisectors and circumcenter. 8. Drag the lowest vertex of the triangle to change its shape. Do not allow this point to pass above the other two vertices. (That will mess up the angle measures.) a. What types of triangles have a circumcenter that lies outside the triangle? b. What types of triangles have a circumcenter that lies inside the triangle? c. What types of triangles have a circumcenter that lies on one side of the triangle? 3 M2 GEOMETRY PACKET 1 FOR UNIT 6 – SECTIONS 5-1, 5-2, 5-3 SEGMENTS IN A TRIANGLE Part 3: Problems Involving Perpendicular Bisectors and Circumcenters ̅̅̅̅̅ Ex 1: Find the measure of 𝐹𝑀. Solution: ̅̅̅̅ is The congruence markings and right angle symbol show that 𝐹𝐾 ̅̅̅̅̅ the perpendicular bisector of 𝐺𝑀 . ̅̅̅̅̅, then F is equidistant Since F is on the perpendicular bisector of 𝐺𝑀 from G and M, or FG = FM. Since FG = 2.8, then FM also measures 2.8. ̅̅̅̅ . Find x. ̅̅̅̅ is the perpendicular bisector of 𝐴𝐶 Ex 2: 𝐵𝐷 Solution: ̅̅̅̅ , then D is the Since B is on the perpendicular bisector of 𝐴𝐶 midpoint of A and C, or DA = DC. 3x + 8 = 5x – 6 14 = 2x 7=x 9. Find each measure. Explain your reasoning. a. XW b. BF 4 M2 GEOMETRY PACKET 1 FOR UNIT 6 – SECTIONS 5-1, 5-2, 5-3 SEGMENTS IN A TRIANGLE Investigation – Angle Bisectors of a Triangle Part 1: Properties of Angle Bisectors 1. Use the Geometry window in Geogebra to answer the questions below: a. Select the Ray Tool (under Line). Make an angle by drawing two rays with the same endpoint. b. Select Angle Bisector (under Perpendicular Line), and click the three points on your angle. A sample diagram is shown at right. c. Make a point anywhere on the angle bisector. d. Select Distance (under Angle). Click on your new point and one ray to measure the distance between them. Then measure the distance from the point to the other ray. e. Drag the point along the angle bisector. What do you notice about the distances? Your observation is described by the Angle Bisector Theorem below. Its converse is also true. Angle Bisector Theorem If a point is on the bisector of an angle, then it is equidistant from the sides of the angle. Converse of Angle Bisector Theorem If a point in the interior of an angle if equidistant from the sides of the angle, then it is on the bisector of the angle. 2. The shortest distance from a point to a line lies on a perpendicular path. In the diagram at right, the shortest ⃗⃗⃗⃗⃗ is DE, and the shortest distance from D distance from D to 𝐴𝐶 ⃗⃗⃗⃗⃗ is DF. to 𝐴𝐵 a. By the definition of an angle bisector, if ⃗⃗⃗⃗⃗ 𝐴𝐷 bisects ∠𝐶𝐴𝐵, then ______ = ______. ⃗⃗⃗⃗⃗ bisects ∠𝐶𝐴𝐵, then ______ = ______. b. By the Angle Bisector Theorem, if 𝐴𝐷 c. By the Converse of the Angle Bisector Theorem, if ______ = ______, then D is on the bisector of ∠𝐶𝐴𝐵. 5 M2 GEOMETRY PACKET 1 FOR UNIT 6 – SECTIONS 5-1, 5-2, 5-3 SEGMENTS IN A TRIANGLE Part 2: The Incenter Pause for a demonstration on the SmartBoard. Incenter Theorem The angle bisectors of a triangle intersect at a point called the incenter that is equidistant from the sides of the triangle. ⃗⃗⃗⃗⃗⃗ is the angle bisector of ∠NMP. Find x if m∠1 = 5x + 8 and m∠2 = 8x – 16. Ex: 𝑀𝑅 Solution: If ⃗⃗⃗⃗⃗⃗ 𝑀𝑅 is the angle bisector of ∠NMP, then m∠1 = m∠2. 5x + 8 = 8x – 16 24 = 3x 8=x 3. Find each measure. Explain your reasoning. a. m∠ABE b. m∠YBA b. MK d. m∠EWL 4. U is the incenter of △GHY. Find each measure. a. MU b. m∠UGM c. m∠PHU d. HU 6 M2 GEOMETRY PACKET 1 FOR UNIT 6 – SECTIONS 5-1, 5-2, 5-3 SEGMENTS IN A TRIANGLE Section 5-2 Medians of a Triangle A median is a line segment that connects a vertex of a triangle to the midpoint of the opposite side. 1. Open the Geogebra worksheet at https://www.geogebra.org/m/nrmv25KY. ∆ABC has been constructed with its three medians. a. If ̅̅̅̅ 𝐴𝐹 , ̅̅̅̅ 𝐵𝐸 , and ̅̅̅̅ 𝐶𝐷 are the three medians of ∆ABC, then: (fill in the blanks) (i) ̅̅̅̅ 𝐹𝐵 ≅ ______ (ii) ̅̅̅̅ 𝐴𝐷 ≅ ______ (iii) ̅̅̅̅ 𝐶𝐸 ≅ ______ b. Drag point A, B, or C to change the shape of the triangle. Then copy the lengths of the segments onto the diagram at right. c. Find each ratio: 𝐴𝐺 𝐹𝐺 𝐵𝐺 𝐸𝐺 𝐶𝐺 𝐷𝐺 = 𝐴𝐺 = 𝐵𝐺 = 𝐶𝐺 𝐴𝐹 𝐵𝐸 𝐶𝐷 = = = d. What do you notice? Compare your results with at least two other people. e. Fill in the blanks: The centroid breaks each median into two segments in the ratio ____ : ____. The segment from a vertex to the centroid is located _______________ of the way from the vertex to the midpoint of the opposite side. 7 M2 GEOMETRY PACKET 1 FOR UNIT 6 – SECTIONS 5-1, 5-2, 5-3 SEGMENTS IN A TRIANGLE Ex: In △ABC, U is the centroid and BU = 16. Find UK and BK. Solution: (Method 1) Since BU is 2/3 of BK, 2 BU = 3 BK. (Method 2) BU is twice UK, or UK is half of BU. Since BU = 16, then UK = 16/2 = 8. 16 = 3 BK BK = BU + UK 2 24 = BK Then, BU + UK = BK 16 + UK = 24 UK = 8 BK = 16 + 8 = 24 2. In △ABC, AU = 16, BU = 12, and CF = 18. Find each measure. a. UD b. EU c. CU d. AD e. UF f. BE 3. In △CDE, U is the centroid, UK = 12, EM = 21, and UD = 9. Find each measure. a. CU b. MU c. CK d. JU e. EU f. JD 8 M2 GEOMETRY PACKET 1 FOR UNIT 6 – SECTIONS 5-1, 5-2, 5-3 SEGMENTS IN A TRIANGLE Section 5-2 Altitudes of a Triangle 1. Open the applet at https://www.geogebra.org/m/Ms2HETdB. 2. The applet shows a triangle and its three altitudes. Notice that the three altitudes intersect at a single point. This point is called the orthocenter. a. Drag the points so that ∆ABC appears to be obtuse. Where is the orthocenter in relation to the triangle? b. Drag the points so that ∆ABC appears to be acute. Where is the orthocenter in relation to the triangle? c. What do you think will happen when the orthocenter sits on a side of the triangle? Test your hypothesis. 3. Fill in the blanks: a. Any point on the perpendicular bisector of a segment is __________________ from the __________________ of the segment. b. The intersection of the three perpendicular bisectors of a triangle is called the __________________________. This point is equidistant from ____________________________ ________________________________. c. Any point on the _____________________ of an angle is equidistant from the _______________ of the angle. d. The intersection of the three _________________________ of a triangle is called the incenter. This point is equidistant from _____________________________________________. e. The intersection of the three _________________________ of a triangle is called the centroid. The centroid breaks each ___________________ into two segments in the ratio ____ : ____, or so that the longer segment is ____/____ of the whole segment. f. The _____________________ is the intersection of the three altitudes of a triangle. 9 M2 GEOMETRY PACKET 1 FOR UNIT 6 – SECTIONS 5-1, 5-2, 5-3 SEGMENTS IN A TRIANGLE Section 5-3 Inequalities in One Triangle 1. a. Which angle is an exterior angle of the triangle shown in the figure at right? b. By the Exterior Angle Theorem, ∠ _______ = ∠ _______ + ∠ _______ c. As a result, the measure of the exterior angle, ∠ _______, must be greater than the measure of ∠ _______ and also must be greater than the measure of ∠ _______. Exterior Angle Inequality Theorem The measure of an exterior angle of a triangle is greater than the measure of either of its corresponding remote interior angles. Ex: List all angles of △EFG with measures less than m∠1. Solution: The measure of an exterior angle is greater than the measure of either remote interior angle. So ∠3 and ∠4 both have measures less than that of ∠1. 2. Use the Exterior Angle Inequality Theorem to list all of the angles that have measures satisfying the stated condition. a. less than m∠1 b. greater than m∠3 c. greater than m∠1 d. less than m∠7 e. greater than m∠5 10 M2 GEOMETRY PACKET 1 FOR UNIT 6 – SECTIONS 5-1, 5-2, 5-3 SEGMENTS IN A TRIANGLE 3. Open the applet at https://www.geogebra.org/m/DbjlQ7jX. a. Drag parts of the triangle to make the side opposite ∠𝐴 the shortest side of the triangle. Which is the smallest angle in the triangle? b. Draw parts of the triangle to make the side opposite ∠𝐴 the longest side of the triangle. Which is the largest angle in the triangle? c. Use your answers from parts (a) and (b) above to list the angles of ∆𝑅𝑆𝑇 in order from LEAST to GREATEST. d. List the sides of ∆𝐴𝐵𝐶 in order from LEAST to GREATEST. 4. List the angles and sides in order from smallest to largest. a. b. 11 M2 GEOMETRY PACKET 1 FOR UNIT 6 – SECTIONS 5-1, 5-2, 5-3 SEGMENTS IN A TRIANGLE Review of 5-1 to 5-3 In each problem, determine whether the diagram shows a perpendicular bisector or an angle bisector. Then find the requests measure. 1. FG 2. m∠MYW 3. m∠LYF 4. TU 5. IU 6. KL P is the circumcenter of △ABC. List any segment(s) congruent to each segment. ̅̅̅̅ 7. 𝐵𝑅 8. ̅̅̅̅ 𝐶𝑆 9. ̅̅̅̅ 𝐵𝑃 12 M2 GEOMETRY PACKET 1 FOR UNIT 6 – SECTIONS 5-1, 5-2, 5-3 SEGMENTS IN A TRIANGLE A is the incenter of △PQR. Find each measure. 10. m∠ARU 11. AU 12. m∠QPK 13. A triangular entranceway has walls with corner angles of 50°, 70°, and 60°.The designer wants to place a tall bronze sculpture on a round pedestal in a central location equidistant from the three walls. How can the designer find where to place the sculpture? In △PQR, NQ = 6, RK = 3, and PK = 4. Find each measure. 14. KM 15. KQ 16. LK 17. LR 18. NK 19. PM In △STR, H is the centroid, EH = 6, DH = 4, and SM = 24. Find each measure. 20. SH 21. HM 22. TH 23. HR 24. TD 25. ER 13 M2 GEOMETRY PACKET 1 FOR UNIT 6 – SECTIONS 5-1, 5-2, 5-3 SEGMENTS IN A TRIANGLE Use the Exterior Angle Inequality Theorem to list all of the angles that satisfy the stated condition. 26. measures less than m∠ 1 27. measures less than m∠ 9 28. measures greater than m∠ 5 29. measures greater than m∠ 8 List the angles and sides of each triangle in order from smallest to largest 30. 31. 32. 33. Use the figure at the right to determine which angle in each list has the greatest measure. 34. ∠1, ∠3, ∠4 35. ∠4, ∠8, ∠9 35. ∠2, ∠3, ∠7 36. ∠7, ∠8, ∠10 14 M2 GEOMETRY PACKET 1 FOR UNIT 6 – SECTIONS 5-1, 5-2, 5-3 SEGMENTS IN A TRIANGLE Use the figure at the right to determine the relationship between the measures of the given angles. Fill in the blank with <, =, or >. 37. m∠ QRW ____ m∠ RWQ 38. m∠ RTW ____ m∠ TWR 39. m∠ RST ____ m∠ TRS 40. m∠ WQR ____ m∠ QRW Use the figure at the right to determine the relationship between the lengths of the given sides. Fill in the blank with <, =, or >. 41. DH____GH 42. DE ____ DG 43. EG____ FG 44. DE____ EG 45. The circumcenter is found by constructing the ___________________ ________________ of each side of the triangle. 46. The circumcenter of a triangle is equidistant from the ___________________ of the triangle. 47. The perpendicular bisectors of the sides of an ____________ triangle intersect outside the triangle. 48. The perpendicular bisectors of the sides of an ____________ triangle intersect inside the triangle. 49. The perpendicular bisectors of the sides of a ____________ triangle intersect on the hypotenuse of the triangle. 50. The incenter is found by constructing the _________________ of each _________________ of a triangle. 51. The incenter is equidistant from the _________________ of the triangle. 52. The centroid is found by constructing the __________________ of a triangle. 53. The centroid breaks each median into two segments in the ratio ____ : ____. The longer of these segments is _________-_____________ of the length of the median. 54. The orthocenter is found by constructing the _________________ of a triangle. 15