* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Chapter 1 Introduction: Matter and Measurement
Analytical chemistry wikipedia , lookup
Size-exclusion chromatography wikipedia , lookup
Chemistry: A Volatile History wikipedia , lookup
Chemical bond wikipedia , lookup
History of chemistry wikipedia , lookup
Gas chromatography–mass spectrometry wikipedia , lookup
Fluorescence correlation spectroscopy wikipedia , lookup
Molecular dynamics wikipedia , lookup
Stoichiometry wikipedia , lookup
IUPAC nomenclature of inorganic chemistry 2005 wikipedia , lookup
Lorentz force velocimetry wikipedia , lookup
Matter wave wikipedia , lookup
Rutherford backscattering spectrometry wikipedia , lookup
History of molecular theory wikipedia , lookup
Condensed matter physics wikipedia , lookup
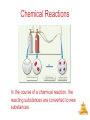
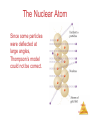
Chemistry, The Central Science, 10th edition Theodore L. Brown; H. Eugene LeMay, Jr.; and Bruce E. Bursten Chapter 1 Introduction: Matter and Measurement Matter And Measurement Chemistry: The study of matter and the changes it undergoes. Matter And Measurement Scientific Method: A systematic approach to solving problems. Matter And Measurement Matter: Anything that has mass and takes up space. Matter And Measurement Periodic Table of the Elements 118 elements now, there will be more…. Elements: alphabet of chemistry language Matter And Measurement Matter • Atoms are the building blocks of matter. Matter And Measurement Matter • Atoms are the building blocks of matter. • Each element is made of the same kind of atom. Matter And Measurement Matter • Atoms are the building blocks of matter. • Each element is made of the same kind of atom. • A compound is made of two or more different kinds of Matter elements. And Measurement States of Matter Matter And Measurement Distance between molecules Motion freedom of the molecules Gas Very large Free Liquid Small Partially free (flow) Solid Very small Fixed in a certain positions Gas: The shape and volume depend on the container. Solid: have specific shape and volume. Matter And Measurement Classification of Matter Matter And Measurement Classification of Matter Matter And Measurement Classification of Matter Matter And Measurement Classification of Matter Matter And Measurement Classification of Matter Matter And Measurement Classification of Matter Matter And Measurement Classification of Matter Matter And Measurement Classification of Matter Matter And Measurement Classification of Matter Matter And Measurement Classification of Matter Matter And Measurement Matter And Measurement Matter And Measurement Mixtures and Compounds Matter And Measurement Properties and Changes of Matter Matter And Measurement Properties of Matter • Physical Properties: □ Can be observed without changing a substance into another substance. • Boiling point, density, mass, volume, etc. • Chemical Properties: □ Can only be observed when a substance is changed into another substance. • Flammability, corrosiveness, reactivity with acid, Matter etc. And Measurement Properties of Matter • Intensive Properties: □ Independent of the amount of the substance that is present. • Density, boiling point, color, etc. • Extensive Properties: □ Dependent upon the amount of the substance present. • Mass, volume, energy, etc. Matter And Measurement Changes of Matter • Physical Changes: □ Changes in matter that do not change the composition of a substance. • Changes of state, temperature, volume, etc. • Chemical Changes: □ Changes that result in new substances. • Combustion, oxidation, decomposition, etc. Matter And Measurement Chemical Reactions In the course of a chemical reaction, the reacting substances are converted to new substances. Matter And Measurement Chemical Reactions Matter And Measurement Compounds Compounds can be broken down into more elemental particles. Matter And Measurement Electrolysis of Water Matter And Measurement Separation of Mixtures Matter And Measurement Distillation: Separates homogeneous mixture on the basis of differences in boiling point. Matter And Measurement Distillation Matter And Measurement Filtration: Separates solid substances from liquids and solutions. Matter And Measurement Chromatography: Separates substances on the basis of differences in solubility in a solvent. Matter And Measurement Units of Measurement Matter And Measurement SI Units • Système International d’Unités • Uses a different base unit for each quantity Matter And Measurement Metric System Prefixes convert the base units into units that are appropriate for the item being measured. Matter And Measurement Matter And Measurement Volume • The most commonly used metric units for volume are the liter (L) and the milliliter (mL). □ A liter is a cube 1 dm long on each side. □ A milliliter is a cube 1 cm long on each side. Matter And Measurement Uncertainty in Measurements Different measuring devices have different uses and different degrees of accuracy. Matter And Measurement Temperature: A measure of the average kinetic energy of the particles in a sample. Matter And Measurement Temperature • In scientific measurements, the Celsius and Kelvin scales are most often used. • The Celsius scale is based on the properties of water. □ 0℃ is the freezing point of water. □ 100 ℃ is the boiling point of water. Matter And Measurement Temperature • The Kelvin is the SI unit of temperature. • It is based on the properties of gases. • There are no negative Kelvin temperatures. • K = ℃ + 273.15 Matter And Measurement Temperature • The Fahrenheit scale is not used in scientific measurements. • F = 9/5(℃) + 32 • ℃ = 5/9(F − 32) Matter And Measurement Matter And Measurement Density: Physical property of a substance m d= V Matter And Measurement Matter And Measurement Uncertainty in Measurement Matter And Measurement Accuracy versus Precision • Accuracy refers to the proximity of a measurement to the true value of a quantity. • Precision refers to the proximity of several measurements to each other. Matter And Measurement Matter And Measurement Matter And Measurement Significant Figures • The term significant figures refers to digits that were measured. • When rounding calculated numbers, we pay attention to significant figures so we do not overstate the accuracy of our answers. Matter And Measurement Matter And Measurement Significant Figures 1. All nonzero digits are significant. 2. Zeroes between two significant figures are themselves significant. 3. Zeroes at the beginning of a number are never significant. 4. Zeroes at the end of a number are significant if a decimal point is written Matter in the number. And Measurement Matter And Measurement Significant Figures • When addition or subtraction is performed, answers are rounded to the least significant decimal place. Matter And Measurement • When multiplication or division is performed, answers are rounded to the number of digits that corresponds to the least number of significant figures in any of the numbers used in the calculation Matter And Measurement Matter And Measurement Matter And Measurement Matter And Measurement Dimensional Analysis Conversion factor Matter And Measurement Matter And Measurement Using Two or More Conversion Factors Matter And Measurement Matter And Measurement Matter And Measurement Conversions Involving Volume Q: Calculate the mass in grams of 2 cubic inches, the density of gold is 19.3g/cm3 Conversion factor Matter And Measurement Matter And Measurement Matter And Measurement Matter And Measurement Chemistry, The Central Science, 10th edition Theodore L. Brown; H. Eugene LeMay, Jr.; and Bruce E. Bursten Chapter 2 Atoms, Molecules, and Ions Matter And Measurement Atomic Theory of Matter The theory that atoms are the fundamental building blocks of matter reemerged in the early 19th century, championed by John Dalton. Matter And Measurement Dalton’s Postulates Each element is composed of extremely small particles called atoms. Matter And Measurement Dalton’s Postulates All atoms of a given element are identical to one another in mass and other properties, but the atoms of one element are different from the atoms of all other elements. Matter And Measurement Dalton’s Postulates Atoms of an element are not changed into atoms of a different element by chemical reactions; atoms are neither created nor destroyed in chemical reactions. Matter And Measurement Dalton’s Postulates Compounds are formed when atoms of more than one element combine; a given compound always has the same relative number and kind of atoms. Matter And Measurement Law of Constant Composition Joseph Proust (1754–1826) • Also known as the law of definite proportions. • The elemental composition of a pure substance never varies. Matter And Measurement Multiple Proportions Matter And Measurement Multiple Proportions Matter And Measurement Law of Conservation of Mass The total mass of substances present at the end of a chemical process is the same as the mass of substances present before the process took place. Matter And Measurement • Particles with the some charge repel one another. • Particles with unlike charges attract one another. Matter And Measurement The Electron • Streams of negatively charged particles were found to emanate from cathode tubes. • J. J. Thompson is credited with their Matter discovery (1897). And Measurement The Electron Thompson measured the charge/mass ratio of the electron to be 1.76X108 coulombs/g. Matter And Measurement Millikan Oil Drop Experiment Once the charge/mass ratio of the electron was known, determination of either the charge or the mass of an electron would yield the other. Matter And Measurement Millikan Oil Drop Experiment Robert Millikan (University of Chicago) determined the charge on the electron in 1909. Matter And Measurement Radioactivity: • The spontaneous emission of radiation by an atom. • First observed by Henri Becquerel. • Also studied by Marie and Pierre Curie. Matter And Measurement Radioactivity • Three types of radiation were discovered by Ernest Rutherford: Matter And Measurement The Atom, circa 1900: • “Plum pudding” model, put forward by Thompson. • Positive sphere of matter with negative electrons imbedded in it. Matter And Measurement Discovery of the Nucleus Ernest Rutherford shot α particles at a thin sheet of gold foil and observed the pattern of scatter of the particles. Matter And Measurement The Nuclear Atom Since some particles were deflected at large angles, Thompson’s model could not be correct. Matter And Measurement The Nuclear Atom • Rutherford postulated a very small, dense nucleus with the electrons around the outside of the atom. • Most of the volume of the atom is empty space. Matter And Measurement Other Subatomic Particles • Protons were discovered by Rutherford in 1919. • Neutrons were discovered by James Chadwick in 1932. Matter And Measurement Subatomic Particles • Protons and electrons are the only particles that have a charge. • Protons and neutrons have essentially the same mass. • The mass of an electron is so small we ignore it. Matter And Measurement Atomic Mass Unit (amu) The mass of heaviest known atom is 4x10-22g It would be cumbersome to express such small mass in grams 1 amu= 1.66054x10-24g 1/12 of the mass of 12C Matter And Measurement Symbols of Elements Elements are symbolized by one or two letters. Matter And Measurement Atomic Number All atoms of the same element have the same number of protons: The atomic number (Z) Matter And Measurement Atomic Mass The mass of an atom in atomic mass units (amu) is the total number of protons and neutrons in the atom. Matter And Measurement Isotopes: • Atoms of the same element with different masses. • Isotopes have different numbers of neutrons. 11 C 6 12 C 6 13 C 6 14 C 6 Matter And Measurement Isotopes of Hydrogen Matter And Measurement Atomic Mass Atomic and molecular masses can be measured with great accuracy with a mass spectrometer. Matter And Measurement Average Mass • Because in the real world we use large amounts of atoms and molecules, we use average masses in calculations. • Average mass is calculated from the isotopes of an element weighted by their relative abundances. Matter And Measurement Average Mass Matter And Measurement Matter And Measurement Matter And Measurement Periodic Table: • A systematic catalog of elements. • Elements are arranged in order of atomic number. Matter And Measurement Periodicity When one looks at the chemical properties of elements, one notices a repeating pattern of reactivities. Matter And Measurement Periodic Table • The rows on the periodic chart are periods. • Columns are groups. • Elements in the same group have similar chemical properties. Matter And Measurement Groups These five groups are known by their names. Matter And Measurement Periodic Table Nonmetals are on the right side of the periodic table (with the exception of H). Solid, gas , liquid Matter And Measurement Periodic Table Elements around Metalloids border the stair-step line (with the exception of Al and Po). Semi-conductors No luster Matter And Measurement Periodic Table Metals are on the left side of the chart. Metal: luster High electrical and heat conductivity At r.t , all of them are solid (except Hg) Matter And Measurement Matter And Measurement Matter And Measurement Matter And Measurement Chemical Formulas The subscript to the right of the symbol of an element tells the number of atoms of that element in one molecule of the compound. Matter And Measurement Molecular Compounds Molecular compounds are composed of molecules and almost always contain only nonmetals. Matter And Measurement Diatomic Molecules These seven elements occur naturally as molecules containing two atoms. Matter And Measurement Types of Formulas • Empirical formulas give the lowest whole-number ratio of atoms of each element in a compound. • Molecular formulas give the exact number of atoms of each element in a compound. Matter And Measurement Types of Formulas • Structural formulas show the order in which atoms are bonded. • Perspective drawings also show the three-dimensional array of atoms in a compound. Matter And Measurement Matter And Measurement Matter And Measurement Ions • When atoms lose or gain electrons, they become ions. – Cations are positive and are formed by elements on the left side of the periodic chart. – Anions are negative and are formed by elements on the right side of the periodic chart. Matter And Measurement Anion A negative ion. Has gained electrons. Nonmetals can gain electrons. Charge is written as a superscript on the right. F 2O Has gained one electron Has gained two electrons Matter And Measurement Cations l l l l Positive ions. Formed by losing electrons. More protons than electrons. Metals form cations. + K Has lost one electron 2+ Ca Has lost two electrons Matter And Measurement Matter And Measurement Matter And Measurement Predicting Ionic charges • Atoms tend to acquire the electron arrangement of noble gas. • Na(11e) close to the noble gas Ne(10e), so Na is going to lose 1 e, Form Na+ Matter And Measurement Can also use electron dots • If it has a few it loses them • If it has many, it gains enough for octet +3+ Al K 3- F N Matter And Measurement Matter And Measurement Ionic Bonds Ionic compounds (such as NaCl) are generally formed between metals and nonmetals. Matter And Measurement Two Types of Compounds Ionic Compounds • Made of cations and anions. • Metals and nonmetals. • The electrons lost by the cation are gained by the anion. • The cation and anions surround each other. • Smallest piece is a FORMULA UNIT. Matter And Measurement Two Types of Compounds Smallest piece Types of elements State Melting Point Ionic Molecular Formula Unit Molecule Metal and Nonmetal Nonmetals solid Solid, liquid or gas High >300ºC Low <300ºC Matter And Measurement Chemical Formulas • Shows the kind and number of atoms in the smallest piece of a substance. • Molecular formula- number and kinds of atoms in a molecule. • CO2 • C6H12O6 Matter And Measurement Formula Unit • The smallest whole number ratio of atoms in an ionic compound. • Ions surround each other so you can’t say which is hooked to which. Matter And Measurement Charges on ions • For most of Group A elements, location on the Periodic Table can tell what kind of ion they form • Elements in the same group have similar properties. • Including the charge when they are ions. Matter And Measurement Charge in groups 1A, 2A and 3A is the group number 1+ 2+ in 5A, 6A and 7A is3+ 3- 2- 1the group number -8 Matter And Measurement Matter And Measurement Matter And Measurement Writing Formulas • Because compounds are electrically neutral, one can determine the formula of a compound this way: – The charge on the cation becomes the subscript on the anion. – The charge on the anion becomes the subscript on the cation. – If these subscripts are not in the lowest wholenumber ratio, divide them by the greatest common Matter factor. And Measurement Matter And Measurement Matter And Measurement Common Cations Matter And Measurement Common Anions Matter And Measurement Inorganic Nomenclature • Write the name of the cation. • If the anion is an element, change its ending to -ide; if the anion is a polyatomic ion, simply write the name of the polyatomic ion. • If the cation can have more than one possible charge, write the charge as a Roman numeral in parentheses. Matter And Measurement Inorganic Nomenclature Matter And Measurement Patterns in Oxyanion Nomenclature • When there are two oxyanions involving the same element: – The one with fewer oxygens ends in -ite • NO2− : nitrite; SO32− : sulfite – The one with more oxygens ends in -ate • NO3− : nitrate; SO42− : sulfate Matter And Measurement Patterns in Oxyanion Nomenclature • The one with the second fewest oxygens ends in -ite ClO2− : chlorite • The one with the second most oxygens ends in -ate ClO3− : chlorate Matter And Measurement Patterns in Oxyanion Nomenclature • The one with the fewest oxygens has the prefix hypoand ends in -ite ClO− : hypochlorite • The one with the most oxygens has the prefix per- and ends in -ate ClO4− : perchlorate Matter And Measurement Acid Nomenclature • If the anion in the acid ends in -ide, change the ending to -ic acid and add the prefix hydro- : – HCl: hydrochloric acid – HBr: hydrobromic acid – HI: hydroiodic acid Matter And Measurement Acid Nomenclature • If the anion in the acid ends in -ite, change the ending to -ous acid: – HClO: hypochlorous acid – HClO2: chlorous acid Matter And Measurement Acid Nomenclature • If the anion in the acid ends in -ate, change the ending to -ic acid: – HClO3: chloric acid – HClO4: perchloric acid Matter And Measurement Nomenclature of Binary Compounds • The less electronegative atom is usually listed first. • A prefix is used to denote the number of atoms of each element in the compound (monois not used on the first element listed, however.) Matter And Measurement Nomenclature of Binary Compounds • The ending on the more electronegative element is changed to -ide. – CO2: carbon dioxide – CCl4: carbon tetrachloride Matter And Measurement Nomenclature of Binary Compounds If the prefix ends with a or o and the name of the element begins with a vowel, the two successive vowels are often elided into one: N2O5: dinitrogen pentoxide Matter And Measurement Chemistry, The Central Science, 11th edition Theodore L. Brown, H. Eugene LeMay, Jr., and Bruce E. Bursten Chapter 3 Stoichiometry: Calculations with Chemical Formulas and Equations Matter And © 2009, Prentice-Hall, Inc. Measurement Chemical Equations H2 and O2 reactant (starting materials) H2O product(the substance produced in the chemical reaction Matter And © 2009, Prentice-Hall, Inc. Measurement Balancing Equations Law of conservation of mass Matter And © 2009, Prentice-Hall, Inc. Measurement Matter And © 2009, Prentice-Hall, Inc. Measurement Matter And © 2009, Prentice-Hall, Inc. Measurement Matter And © 2009, Prentice-Hall, Inc. Measurement Indicating the states of reactants and products Matter And © 2009, Prentice-Hall, Inc. Measurement Matter And © 2009, Prentice-Hall, Inc. Measurement Matter And © 2009, Prentice-Hall, Inc. Measurement Simple Patterns of Chemical reactivity Combination reaction is also called synthesis reaction Matter And © 2009, Prentice-Hall, Inc. Measurement Matter And © 2009, Prentice-Hall, Inc. Measurement Matter And © 2009, Prentice-Hall, Inc. Measurement Matter And © 2009, Prentice-Hall, Inc. Measurement Matter And © 2009, Prentice-Hall, Inc. Measurement Combustion Reactions • Rapid reactions that produce a flame Hydrocarbons: CxHy Always produce CO2 and water. Matter And © 2009, Prentice-Hall, Inc. Measurement Matter And © 2009, Prentice-Hall, Inc. Measurement Matter And © 2009, Prentice-Hall, Inc. Measurement Formula Weights Matter And © 2009, Prentice-Hall, Inc. Measurement Formula Weight (FW) • A formula weight is the sum of the atomic weights for the atoms in a chemical formula. • So, the formula weight of calcium chloride, CaCl2, would be Ca: 1(40.1 amu) + Cl: 2(35.5 amu) 111.1 amu • Formula weights are generally reported Matter for ionic compounds. And © 2009, Prentice-Hall, Inc. Measurement Molecular Weight (MW) • A molecular weight is the sum of the atomic weights of the atoms in a molecule. • For the molecule ethane, C2H6, the molecular weight would be C: 2(12.0 amu) + H: 6(1.0 amu) 30.0 amu Matter And © 2009, Prentice-Hall, Inc. Measurement Sample Exercise 3.5 Calculating formula Weights Calculate the formula weight of (a) sucrose, C12H22O11 (table sugar), and (b) calcium nitrate, Ca(NO3)2. Solution (a) By adding the atomic weights of the atoms in sucrose, we find the formula weight to be 342.0 amu: (b) If a chemical formula has parentheses, the subscript outside the parentheses is a multiplier for all atoms inside. Thus, for Ca(NO3)2, we have Practice Exercise Calculate the formula weight of (a) Al(OH)3 and (b) CH3OH. Answer: (a) 78.0 amu, (b) 32.0 amu Matter And © 2009, Prentice-Hall, Inc. Measurement Percent Composition One can find the percentage of the mass of a compound that comes from each of the elements in the compound by using this equation: (number of atoms)(atomic weight) % element = (FW of the compound) x 100 Matter And © 2009, Prentice-Hall, Inc. Measurement Percent Composition So the percentage of carbon in ethane is… (2)(12.0 amu) %C = (30.0 amu) 24.0 amu x 100 = 30.0 amu = 80.0% Matter And © 2009, Prentice-Hall, Inc. Measurement Sample Exercise 3.6 Calculating Percentage Composition Calculate the percentage of carbon, hydrogen, and oxygen (by mass) in C 12H22O11. Solution Let’s examine this question using the problem-solving steps in the “Strategies in Chemistry: Problem Solving” essay that appears on the next page. Analyze We are given a chemical formula, C12H22O11, and asked to calculate the percentage by mass of its component elements (C, H, and O). Plan We can use Equation 3.10, relying on a periodic table to obtain the atomic weight of each component element. The atomic weights are first used to determine the formula weight of the compound. (The formula weight of C12H22O11, 342.0 amu, was calculated in Sample Exercise 3.5.) We must then do three calculations, one for each element. Solve Using Equation 3.10, we have Check The percentages of the individual elements must add up to 100%, which they do in this case. We could have used more significant figures for our atomic weights, giving more significant figures for our percentage composition, but we have adhered to our suggested guideline of rounding atomic weights to one digit beyond the decimal point. Practice Exercise Calculate the percentage of nitrogen, by mass, in Ca(NO3)2. Answer: 17.1% Matter And © 2009, Prentice-Hall, Inc. Measurement 1. Calculate the mass of Nitrogen in 378g HCN 2. Mass of Hydrogen in 124 g of Ca(C2H3O2)2 Matter And © 2009, Prentice-Hall, Inc. Measurement Moles Matter And © 2009, Prentice-Hall, Inc. Measurement Avogadro’s Number • 6.02 x 1023 • 1 mole of 12C has a mass of 12 g. Matter And © 2009, Prentice-Hall, Inc. Measurement Molar Mass • By definition, a molar mass is the mass of 1 mol of a substance (i.e., g/mol). – The molar mass of an element is the mass number for the element that we find on the periodic table. – The formula weight (in amu’s) will be the same number as the molar mass (in g/mol). Matter And © 2009, Prentice-Hall, Inc. Measurement Using Moles Moles provide a bridge from the molecular scale to the real-world scale. Matter And © 2009, Prentice-Hall, Inc. Measurement Mole Relationships • One mole of atoms, ions, or molecules contains Avogadro’s number of those particles. • One mole of molecules or formula units contains Avogadro’s number times the number of atoms or Matter ions of each element in the compound. And © 2009, Prentice-Hall, Inc. Measurement Sample Exercise 3.7 Estimating Numbers in Atoms Without using a calculator, arrange the following samples in order of increasing numbers of carbon atoms: 12 g 12C, 1 mol C2H2, 9 1023 molecules of CO2. Solution Analyze We are given amounts of different substances expressed in grams, moles, and number of molecules and asked to arrange the samples in order of increasing numbers of C atoms. Plan To determine the number of C atoms in each sample, we must convert g 12C, 1 mol C2H2, and 9 1023 molecules CO2 all to numbers of C atoms. To make these conversions, we use the definition of mole and Avogadro’s number. Solve A mole is defined as the amount of matter that contains as many units of the matter as there are C atoms in exactly 12 g of 12C. Thus, 12 g of 12C contains 1 mol of C atoms (that is, 6.02 1023 C atoms). One mol of C2H2 contains 6 1023 C2H2 molecules. Because there are two C atoms in each C2H2 molecule, this sample contains 12 1023 C atoms. Because each CO2 molecule contains one C atom, the sample of CO2 contains 9 1023 C atoms. Hence, the order is 12 g 12C (6 1023 C atoms) < 9 1023 CO2 molecules (9 1023 C atoms) < 1 mol C2H2 (12 1023 C atoms). Check We can check our results by comparing the number of moles of C atoms in each sample because the number of moles is proportional to the number of atoms. Thus, 12 g of 12C is 1 mol C; 1 mol of C2H2 contains 2 mol C, and 9 1023 molecules of CO2 contain 1.5 mol C, giving the same order as above: 12 g 12C (1 mol C) < 9 1023 CO molecules (1.5 mol C) < 1 mol C H (2 mol C). 2 2 2 Practice Exercise Without using a calculator, arrange the following samples in order of increasing number of O atoms: 1 mol H2O, 1 mol CO2, 3 1023 molecules O3. Answer: 1 mol H2O (6 1023 O atoms) 3 1023 molecules O3 (9 1023 O atoms) 1 mol CO2 (12 1023 O atoms) Matter And © 2009, Prentice-Hall, Inc. Measurement Sample Exercise 3.8 Converting Moles to Atoms Calculate the number of H atoms in 0.350 mol of C6H12O6. Solution Analyze We are given both the amount of a substance (0.350 mol) and its chemical formula (C 6H12O6). The unknown is the number of H atoms in the sample. Plan Avogadro’s number provides the conversion factor between the number of moles of C 6H12O6 and the number of molecules of C6H12O6. Once we know the number of molecules of C6H12O6, we can use the chemical formula, which tells us that each molecule of C6H12O6 contains 12 H atoms. Thus, we convert moles of C6H12O6 to molecules of C6H12O6 and then determine the number of atoms of H from the number of molecules of C6H12O6: Moles C6H12O6 → molecules C6H12O6 → atoms H Check The magnitude of our answer is reasonable. It is a large number about the magnitude of Avogadro’s number. We can also make the following ballpark calculation: Multiplying 0.35 6 1023 gives about 2 1023 molecules. Multiplying this result by 12 gives 24 1023 = 2.4 1024 H atoms, which agrees with the previous, more detailed calculation. Because we were asked for the number of H atoms, the units of our answer are correct. The given data had three significant figures, so our answer has three significant figures. Matter And © 2009, Prentice-Hall, Inc. Measurement Sample Exercise 3.8 Converting Moles to Atoms Calculate the number of H atoms in 0.350 mol of C6H12O6. Practice Exercise How many oxygen atoms are in (a) 0.25 mol Ca(NO3)2 and (b) 1.50 mol of sodium carbonate? Answer: (a) 9.0 1023, (b) 2.71 1024 Matter And © 2009, Prentice-Hall, Inc. Measurement Sample Exercise 3.9 Calculating Molar Mass What is the mass in grams of 1.000 mol of glucose, C6H12O6? Solution Analyze We are given a chemical formula and asked to determine its molar mass. Plan The molar mass of a substance is found by adding the atomic weights of its component atoms. Solve Because glucose has a formula weight of 180.0 amu, one mole of this substance has a mass of 180.0 g. In other words, C6H12O6 has a molar mass of 180.0 g/mol. Check The magnitude of our answer seems reasonable, and g/mol is the appropriate unit for the molar mass. Comment Glucose is sometimes called dextrose. Also known as blood sugar, glucose is found widely in nature, occurring in honey and fruits. Other types of sugars used as food are converted into glucose in the stomach or liver before the body uses them as energy sources. Because glucose requires no conversion, it is often given intravenously to patients who need immediate nourishment. People who have diabetes must carefully monitor the amount of glucose in their blood (See “Chemistry and Life” box in Section 3.6). Practice Exercise Calculate the molar mass of Ca(NO3)2. Answer: 164.1 g/mol Matter And © 2009, Prentice-Hall, Inc. Measurement Sample Exercise 3.10 Converting Grams to Moles Calculate the number of moles of glucose (C6H12O6) in 5.380 g of C6H12O6. Solution Analyze We are given the number of grams of a substance and its chemical formula and asked to calculate the number of moles. Plan The molar mass of a substance provides the factor for converting grams to moles. The molar mass of C6H12O6 is 180.0 g/mol (Sample Exercise 3.9). Solve Using 1 mol C6H12O6=180.0 g C6H12O6 to write the appropriate conversion factor, we have Check Because 5.380 g is less than the molar mass, a reasonable answer is less than one mole. The units of our answer (mol) are appropriate. The original data had four significant figures, so our answer has four significant figures. Practice Exercise How many moles of sodium bicarbonate (NaHCO3) are in 508 g of NaHCO3? Answer: 6.05 mol NaHCO3 Matter And © 2009, Prentice-Hall, Inc. Measurement Sample Exercise 3.11 Converting Moles to Grams Calculate the mass, in grams, of 0.433 mol of calcium nitrate. Solution Analyze We are given the number of moles and the name of a substance and asked to calculate the number of grams in the sample. Plan To convert moles to grams, we need the molar mass, which we can calculate using the chemical formula and atomic weights. Solve Because the calcium ion is Ca2+ and the nitrate ion is NO3–, calcium nitrate is Ca(NO3)2. Adding the atomic weights of the elements in the compound gives a formula weight of 164.1 amu. Using 1 mol Ca(NO3)2 = 164.1 g Ca(NO3)2 to write the appropriate conversion factor, we have Check The number of moles is less than 1, so the number of grams must be less than the molar mass, 164.1 g. Using rounded numbers to estimate, we have 0.5 150 = 75 g. The magnitude of our answer is reasonable. Both the units (g) and the number of significant figures (3) are correct. Practice Exercise What is the mass, in grams, of (a) 6.33 mol of NaHCO3 and (b) 3.0 10–5 mol of sulfuric acid? Answer: (a) 532 g, (b) 2.9 10–3 g Matter And © 2009, Prentice-Hall, Inc. Measurement Sample Exercise 3.12 Calculating the Number of Molecules and Number of Atoms from Mass (a) How many glucose molecules are in 5.23 g of C6H12O6? (b) How many oxygen atoms are in this sample? Solution Analyze We are given the number of grams and the chemical formula and asked to calculate (a) the number of molecules and (b) the number of O atoms in the sample. (a) Plan The strategy for determining the number of molecules in a given quantity of a substance is summarized in Figure 3.10. We must convert 5.23 g C6H12O6 to moles C6H12O6, which can then be converted to molecules C6H12O6. The first conversion uses the molar mass of C6H12O6: 1 mol C6H12O6 = 180.0 g C6H12O6. The second conversion uses Avogadro’s number. Solve Molecules C6H12O6 Check The magnitude of the answer is reasonable. Because the mass we began with is less than a mole, there should be fewer than 6.02 1023 molecules. We can make a ballpark estimate of the answer: 5/200 = 2.5 10–2 mol; 2.5 10–2 6 1023 = 15 1021 = 1.5 1022 molecules. The units (molecules) and significant figures (three) are appropriate. Matter And © 2009, Prentice-Hall, Inc. Measurement Sample Exercise 3.12 Calculating the Number of Molecules and Number of Atoms from Mass Solution (continued) (b) Plan To determine the number of O atoms, we use the fact that there are six O atoms in each molecule of C6H12O6. Thus, multiplying the number of molecules C6H12O6 by the factor (6 atoms O/1 molecule C6H12O6) gives the number of O atoms. Solve Check The answer is simply 6 times as large as the answer to part (a). The number of significant figures (three) and the units (atoms O) are correct. Practice Exercise (a) How many nitric acid molecules are in 4.20 g of HNO3? (b) How many O atoms are in this sample? Answer: (a) 4.01 1022 molecules HNO3, (b) 1.20 1023 atoms O Matter And © 2009, Prentice-Hall, Inc. Measurement Finding Empirical Formulas Matter And © 2009, Prentice-Hall, Inc. Measurement Calculating Empirical Formulas One can calculate the empirical formula from the percent composition. Matter And © 2009, Prentice-Hall, Inc. Measurement Calculating Empirical Formulas The compound para-aminobenzoic acid (you may have seen it listed as PABA on your bottle of sunscreen) is composed of carbon (61.31%), hydrogen (5.14%), nitrogen (10.21%), and oxygen (23.33%). Find the empirical formula of PABA. Matter And © 2009, Prentice-Hall, Inc. Measurement Calculating Empirical Formulas Assuming 100.00 g of para-aminobenzoic acid, C: H: N: O: 1 mol 12.01 g 1 mol 5.14 g x 1.01 g 1 mol 10.21 g x 14.01 g 1 mol 23.33 g x 16.00 g 61.31 g x = 5.105 mol C = 5.09 mol H = 0.7288 mol N = 1.456 mol O Matter And © 2009, Prentice-Hall, Inc. Measurement Calculating Empirical Formulas Calculate the mole ratio by dividing by the smallest number of moles: C: 5.105 mol 0.7288 mol = 7.005 H: 5.09 mol 0.7288 mol = 6.984 N: 0.7288 mol 0.7288 mol = 1.000 O: 1.458 mol 0.7288 mol = 2.001 Matter And © 2009, Prentice-Hall, Inc. Measurement Calculating Empirical Formulas These are the subscripts for the empirical formula: C7H7NO2 Matter And © 2009, Prentice-Hall, Inc. Measurement Sample Exercise 3.13 Calculating Empirical Formula Ascorbic acid (vitamin C) contains 40.92% C, 4.58% H, and 54.50% O by mass. What is the empirical formula of ascorbic acid? Solution Analyze We are to determine an empirical formula of a compound from the mass percentages of its elements. Plan The strategy for determining the empirical formula involves the three steps given in Figure 3.11. Solve We first assume, for simplicity, that we have exactly 100 g of material (although any mass can be used). In 100 g of ascorbic acid, therefore, we have Second, we calculate the number of moles of each element: Third, we determine the simplest whole-number ratio of moles by dividing each number of moles by the smallest number of moles, 3.406: Matter And © 2009, Prentice-Hall, Inc. Measurement Sample Exercise 3.13 Calculating Empirical Formula Solution (continued) The ratio for H is too far from 1 to attribute the difference to experimental error; in fact, it is quite close to 1 1/3. This suggests that if we multiply the ratio by 3, we will obtain whole numbers: The whole-number mole ratio gives us the subscripts for the empirical formula: Check It is reassuring that the subscripts are moderately sized whole numbers. Otherwise, we have little by which to judge the reasonableness of our answer. Practice Exercise A 5.325-g sample of methyl benzoate, a compound used in the manufacture of perfumes, contains 3.758 g of carbon, 0.316 g of hydrogen, and 1.251 g of oxygen. What is the empirical formula of this substance? Answer: C4H4O Matter And © 2009, Prentice-Hall, Inc. Measurement Sample Exercise 3.14 Determining a Molecular Formula Mesitylene, a hydrocarbon that occurs in small amounts in crude oil, has an empirical formula of C 3H4. The experimentally determined molecular weight of this substance is 121 amu. What is the molecular formula of mesitylene? Solution Analyze We are given an empirical formula and a molecular weight and asked to determine a molecular formula. Plan The subscripts in the molecular formula of a compound are whole-number multiples of the subscripts in its empirical formula. To find the appropriate multiple, we must compare the molecular weight with the formula weight of the empirical formula. Solve First, we calculate the formula weight of the empirical formula, C 3H4: 3(12.0 amu) + 4(1.0 amu) = 40.0 amu Next, we divide the molecular weight by the empirical formula weight to obtain the multiple used to multiply the subscripts in C 3H4: Only whole-number ratios make physical sense because we must be dealing with whole atoms. The 3.02 in this case could result from a small experimental error in the molecular weight. We therefore multiply each subscript in the empirical formula by 3 to give the molecular formula: C 9H12. Matter And © 2009, Prentice-Hall, Inc. Measurement Sample Exercise 3.14 Determining a Molecular Formula Solution Check We can have confidence in the result because dividing the molecular weight by the formula weight yields nearly a whole number. Practice Exercise Ethylene glycol, the substance used in automobile antifreeze, is composed of 38.7% C, 9.7% H, and 51.6% O by mass. Its molar mass is 62.1 g/mol. (a) What is the empirical formula of ethylene glycol? (b) What is its molecular formula? Answers: (a) CH3O, (b) C2H6O2 Matter And © 2009, Prentice-Hall, Inc. Measurement Combustion Analysis • Compounds containing C, H and O are routinely analyzed through combustion in a chamber like this. – C is determined from the mass of CO2 produced. – H is determined from the mass of H2O produced. – O is determined by difference after the C and H have been determined. Matter And Measurement © 2009, Prentice-Hall, Inc. Sample Exercise 3.15 Determining Empirical Formula by Combustion Analysis Isopropyl alcohol, a substance sold as rubbing alcohol, is composed of C, H, and O. Combustion of 0.255 g of isopropyl alcohol produces 0.561 g of CO2 and 0.306 g of H2O. Determine the empirical formula of isopropyl alcohol. Solution Analyze We are told that isopropyl alcohol contains C, H, and O atoms and given the quantities of CO 2 and H2O produced when a given quantity of the alcohol is combusted. We must use this information to determine the empirical formula for isopropyl alcohol, a task that requires us to calculate the number of moles of C, H, and O in the sample. Plan We can use the mole concept to calculate the number of grams of C present in the CO 2 and the number of grams of H present in the H2O. These amounts are the quantities of C and H present in the isopropyl alcohol before combustion. The number of grams of O in the compound equals the mass of the isopropyl alcohol minus the sum of the C and H masses. Once we have the number of grams of C, H, and O in the sample, we can then proceed as in Sample Exercise 3.13. We can calculate the number of moles of each element, and determine the mole ratio, which gives the subscripts in the empirical formula. Solve To calculate the number of grams of C, we first use the molar mass of CO2, 1 mol CO2 = 44.0 g CO2, to convert grams of CO2 to moles of CO2. Because each CO2 molecule has only 1 C atom, there is 1 mol of C atoms per mole of CO2 molecules. This fact allows us to convert the moles of CO2 to moles of C. Finally, we use the molar mass of C, 1 mol C =1 2.0 g C, to convert moles of C to grams of C. Combining the three conversion factors, we have Matter And © 2009, Prentice-Hall, Inc. Measurement Sample Exercise 3.15 Determining Empirical Formula by Combustion Analysis Solution (continued) The calculation of the number of grams of H from the grams of H2O is similar, although we must remember that there are 2 mol of H atoms per 1 mol of H2O molecules: The total mass of the sample, 0.255 g, is the sum of the masses of the C, H, and O. Thus, we can calculate the mass of O as follows: We then calculate the number of moles of C, H, and O in the sample: To find the empirical formula, we must compare the relative number of moles of each element in the sample. The relative number of moles of each element is found by dividing each number by the smallest number, 0.0043. The mole ratio of C:H:O so obtained is 2.98:7.91:1.00. The first two numbers are very close to the whole numbers 3 and 8, giving the empirical formula C 3H8O. Check The subscripts work out to be moderately sized whole numbers, as expected. Matter And © 2009, Prentice-Hall, Inc. Measurement Sample Exercise 3.15 Determining Empirical Formula by Combustion Analysis Practice Exercise (a) Caproic acid, which is responsible for the foul odor of dirty socks, is composed of C, H, and O atoms. Combustion of a 0.225-g sample of this compound produces 0.512 g CO2 and 0.209 g H2O. What is the empirical formula of caproic acid? (b) Caproic acid has a molar mass of 116 g/mol. What is its molecular formula? Answers: (a) C3H6O, (b) C6H12O2 Matter And © 2009, Prentice-Hall, Inc. Measurement Elemental Analyses Compounds containing other elements are analyzed using methods analogous to those used for C, H and O. Matter And © 2009, Prentice-Hall, Inc. Measurement Stoichiometric Calculations The coefficients in the balanced equation give the ratio of moles of reactants and products. Matter And © 2009, Prentice-Hall, Inc. Measurement Stoichiometric Calculations Starting with the mass of Substance A you can use the ratio of the coefficients of A and B to calculate the mass of Substance B formed (if it’s a product) or used (if it’s a reactant). Matter And © 2009, Prentice-Hall, Inc. Measurement Stoichiometric Calculations C6H12O6 + 6 O2 6 CO2 + 6 H2O Starting with 1.00 g of C6H12O6… we calculate the moles of C6H12O6… use the coefficients to find the moles of H2O… and then turn the moles of water to grams. Matter And © 2009, Prentice-Hall, Inc. Measurement Sample Exercise 3.16 Calculating Amounts of Reactants and Products How many grams of water are produced in the oxidation of 1.00 g of glucose, C 6H12O6? C6H12O6(s) + 6 O2(g)→6 CO2(g) + 6 H2O(l) Solution Analyze We are given the mass of a reactant and are asked to determine the mass of a product in the given equation. Plan The general strategy, as outlined in Figure 3.13, requires three steps. First, the amount of C 6H12O6 must be converted from grams to moles. Second, we can use the balanced equation, which relates the moles of C6H12O6 to the moles of H2O: 1 mol C6H12O6 6 mol H2O. Third, we must convert the moles of H2O to grams. Solve First, use the molar mass of C6H12O6 to convert from grams C6H12O6 to moles C6H12O6: Second, use the balanced equation to convert moles of C6H12O6 to moles of H2O: Third, use the molar mass of H2O to convert from moles of H2O to grams of H2O: The steps can be summarized in a diagram like that in Figure 3.13: Matter And © 2009, Prentice-Hall, Inc. Measurement Sample Exercise 3.16 Calculating Amounts of Reactants and Products Solution (continued) Check An estimate of the magnitude of our answer, 18/180 = 0.1 and 0.1 6 = 0.6, agrees with the exact calculation. The units, grams H2O, are correct. The initial data had three significant figures, so three significant figures for the answer is correct. Comment An average person ingests 2 L of water daily and eliminates 2.4 L. The difference between 2 L and 2.4 L is produced in the metabolism of foodstuffs, such as in the oxidation of glucose. (Metabolism is a general term used to describe all the chemical processes of a living animal or plant.) The desert rat (kangaroo rat), on the other hand, apparently never drinks water. It survives on its metabolic water. Practice Exercise The decomposition of KClO3 is commonly used to prepare small amounts of O2 in the laboratory: 2 KClO3(s) → 2 KCl(s) + 3 O2(g). How many grams of O2 can be prepared from 4.50 g of KClO3? Answer: 1.77 g Matter And © 2009, Prentice-Hall, Inc. Measurement Limiting Reactants Matter And © 2009, Prentice-Hall, Inc. Measurement How Many Cookies Can I Make? • You can make cookies until you run out of one of the ingredients. • Once this family runs out of sugar, they will stop making cookies (at least any cookies you would want to eat). Matter And © 2009, Prentice-Hall, Inc. Measurement How Many Cookies Can I Make? • In this example the sugar would be the limiting reactant, because it will limit the amount of cookies you can make. Matter And © 2009, Prentice-Hall, Inc. Measurement Limiting Reactants • The limiting reactant is the reactant present in the smallest stoichiometric amount. – In other words, it’s the reactant you’ll run out of first (in this case, the H2). Matter And © 2009, Prentice-Hall, Inc. Measurement Limiting Reactants In the example below, the O2 would be the excess reagent. Matter And © 2009, Prentice-Hall, Inc. Measurement Sample Exercise 3.18 Calculating the Amount of Product Formed from a Limiting Reactant The most important commercial process for converting N2 from the air into nitrogen-containing compounds is based on the reaction of N2 and H2 to form ammonia (NH3): N2(g) + 3 H2(g)→2 NH3(g) How many moles of NH3 can be formed from 3.0 mol of N2 and 6.0 mol of H2? Solution Analyze We are asked to calculate the number of moles of product, NH3, given the quantities of each reactant, N2 and H2, available in a reaction. Thus, this is a limiting reactant problem. Plan If we assume that one reactant is completely consumed, we can calculate how much of the second reactant is needed in the reaction. By comparing the calculated quantity with the available amount, we can determine which reactant is limiting. We then proceed with the calculation, using the quantity of the limiting reactant. Solve The number of moles of H2 needed for complete consumption of 3.0 mol of N2 is: Because only 6.0 mol H2 is available, we will run out of H2 before the N2 is gone, and H2 will be the limiting reactant. We use the quantity of the limiting reactant, H2, to calculate the quantity of NH3 produced: Comment The table on the right summarizes this example: Matter And © 2009, Prentice-Hall, Inc. Measurement Sample Exercise 3.18 Calculating the Amount of Product Formed from a Limiting Reactant Solution (continued) Notice that we can calculate not only the number of moles of NH 3 formed but also the number of moles of each of the reactants remaining after the reaction. Notice also that although the number of moles of H 2 present at the beginning of the reaction is greater than the number of moles of N 2 present, the H2 is nevertheless the limiting reactant because of its larger coefficient in the balanced equation. Check The summarizing table shows that the mole ratio of reactants used and product formed conforms to the coefficients in the balanced equation, 1:3:2. Also, because H 2 is the limiting reactant, it is completely consumed in the reaction, leaving 0 mol at the end. Because 6.0 mol H 2 has two significant figures, our answer has two significant figures. Practice Exercise Consider the reaction 2 Al(s) + 3 Cl2(g) → 2 AlCl3(s). A mixture of 1.50 mol of Al and 3.00 mol of Cl2 is allowed to react. (a) Which is the limiting reactant? (b) How many moles of AlCl3 are formed? (c) How many moles of the excess reactant remain at the end of the reaction? Answers: (a) Al, (b) 1.50 mol, (c) 0.75 mol Cl2 Matter And © 2009, Prentice-Hall, Inc. Measurement Sample Exercise 3.19 Calculating the Amount of Product Formed from a Limiting Reactant Solution (continued) Thus, there are more moles of H2 than O2. The coefficients in the balanced equation indicate, however, that the reaction requires 2 moles of H2 for every 1 mole of O2. Therefore, to completely react all the O2, we would need 2 47 = 94 moles of H2. Since there are only 75 moles of H2, H2 is the limiting reagent. We therefore use the quantity of H2 to calculate the quantity of product formed. We can begin this calculation with the grams of H2, but we can save a step by starting with the moles of H2 that were calculated previously in the exercise: Check The magnitude of the answer seems reasonable. The units are correct, and the number of significant figures (two) corresponds to those in the numbers of grams of the starting materials. Comment The quantity of the limiting reagent, H2, can also be used to determine the quantity of O2 used (37.5 mol = 1200 g). The number of grams of the excess oxygen remaining at the end of the reaction equals the starting amount minus the amount consumed in the reaction, 1500 g – 1200 g = 300 g. Practice Exercise A strip of zinc metal with a mass of 2.00 g is placed in an aqueous solution containing 2.50 g of silver nitrate, causing the following reaction to occur: Zn(s) + 2 AgNO3(aq) → 2 Ag(s) + Zn(NO3)2(aq) Matter And © 2009, Prentice-Hall, Inc. Measurement Sample Exercise 3.19 Calculating the Amount of Product Formed from a Limiting Reactant Practice Exercise (continued) (a) Which reactant is limiting? (b) How many grams of Ag will form? (c) How many grams of Zn(NO3)2 will form? (d) How many grams of the excess reactant will be left at the end of the reaction? Answers: (a) AgNO3, (b) 1.59 g, (c) 1.39 g, (d) 1.52 g Zn Matter And © 2009, Prentice-Hall, Inc. Measurement Theoretical Yield • The theoretical yield is the maximum amount of product that can be made. – In other words it’s the amount of product possible as calculated through the stoichiometry problem. • This is different from the actual yield, which is the amount one actually produces and measures. Matter And © 2009, Prentice-Hall, Inc. Measurement Percent Yield One finds the percent yield by comparing the amount actually obtained (actual yield) to the amount it was possible to make (theoretical yield). Actual Yield Percent Yield = Theoretical Yield x 100 Matter And © 2009, Prentice-Hall, Inc. Measurement Sample Exercise 3.20 Calculating the Theoretical Yield and the Percent Yield for a Reaction Adipic acid, H2C6H8O4, is used to produce nylon. The acid is made commercially by a controlled reaction between cyclohexane (C6H12) and O2: 2 C6H12(l) + 5 O2(g) → 2 H2C6H8O4(l) + 2 H2O(g) (a) Assume that you carry out this reaction starting with 25.0 g of cyclohexane and that cyclohexane is the limiting reactant. What is the theoretical yield of adipic acid? (b) If you obtain 33.5 g of adipic acid from your reaction, what is the percent yield of adipic acid? Solution Analyze We are given a chemical equation and the quantity of the limiting reactant (25.0 g of C 6H12). We are asked first to calculate the theoretical yield of a product (H 2C6H8O4) and then to calculate its percent yield if only 33.5 g of the substance is actually obtained. Plan (a) The theoretical yield, which is the calculated quantity of adipic acid formed in the reaction, can be calculated using the following sequence of conversions: g C6H12 → mol C6H12 → mol H2C6H8O4 → g H2C6H8O4 Matter And © 2009, Prentice-Hall, Inc. Measurement Sample Exercise 3.20 Calculating the Theoretical Yield and the Percent Yield for a Reaction Solution (continued) (b) The percent yield is calculated by comparing the actual yield (33.5 g) to the theoretical yield using Equation 3.14. Solve Check Our answer in (a) has the appropriate magnitude, units, and significant figures. In (b) the answer is less than 100% as necessary. Practice Exercise Imagine that you are working on ways to improve the process by which iron ore containing Fe 2O3 is converted into iron. In your tests you carry out the following reaction on a small scale: Fe2O3(s) + 3 CO(g) → 2 Fe(s) + 3 CO2(g) (a) If you start with 150 g of Fe2O3 as the limiting reagent, what is the theoretical yield of Fe? (b) If the actual yield of Fe in your test was 87.9 g, what was the percent yield? Answers: (a) 105 g Fe, (b) 83.7% Matter And © 2009, Prentice-Hall, Inc. Measurement