Download Fermat`s Last Theorem - Math @ McMaster University

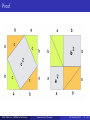
Matt Valeriote (McMaster University)
Fermat’s Last Theorem
26 January, 2017
1 / 14
Fermat’s Last Theorem
Matt Valeriote
McMaster University
26 January, 2017
Matt Valeriote (McMaster University)
Fermat’s Last Theorem
26 January, 2017
2 / 14
The Pythagorean Theorem
Theorem
The square of the hypotenuse of a right angle
triangle is equal to the sum of the squares of
the other two sides.
Note
In other words, if we have a right angle triangle with
c = the length of the hypotenuse, and
a and b are the lengths of the other two sides, then
a2 + b 2 = c 2 .
Matt Valeriote (McMaster University)
Fermat’s Last Theorem
26 January, 2017
3 / 14
Proof
Matt Valeriote (McMaster University)
Fermat’s Last Theorem
26 January, 2017
4 / 14
Pythagorean Triples
Pythagorean triples
Any triple of natural numbers (a, b, c) that satisfy a2 + b 2 = c 2 is called a
Pythagorean triple.
Note
So, the following are Pythagorean triples:
(3, 4, 5),
(5, 12, 13),
(8, 15, 17),
(9, 12, 15).
Definition
A Pythagorean triple (a, b, c) is primitive if the number 1 is the only
common divisor of a, b, and c, i.e, they are relatively prime.
Matt Valeriote (McMaster University)
Fermat’s Last Theorem
26 January, 2017
5 / 14
The Pythagorean Triples Theorem
Note
There are an infinite number of (primitive) Pythagorean triples, and the
following theorem provides a way to generate all of them.
Theorem
Let m > n be relatively prime natural numbers with one of them even, and
one of them odd. Then
(2mn, m2 − n2 , m2 + n2 ) is a primitive Pythagorean triple, and
Every primitive Pythagorean triple is of this form.
Notes
It follows that if (a, b, c) is a primitive Pythagorean triple, then c is
odd, and exactly one of a and b is even,
and every Pythagorean triple is of the form:
(k · (2mn), k · (m2 − n2 ), k · (m2 + n2 )) for some integer k.
Matt Valeriote (McMaster University)
Fermat’s Last Theorem
26 January, 2017
6 / 14
Fermat’s Last Theorem
Note
In contrast to the equation x 2 + y 2 = z 2 , which we have seen has an
infinite number of solutions over the natural numbers, the cases where we
replace the exponent 2 in this equation with larger exponents is strikingly
different.
Fermat’s Last Theorem
If n > 2 then there are no positive integers a, b, and c such that
an + b n = c n .
Notes
This theorem was claimed by Pierre de Fermat in 1637, but he did
not provide a general proof.
Fermat did provide a proof for the case n = 4.
In 1994 Andrew Wiles produced a proof of the full theorem.
Matt Valeriote (McMaster University)
Fermat’s Last Theorem
26 January, 2017
7 / 14
A Reduction
Note
Suppose that the triple (a, b, c) is a solution to the equation
x 15 + y 15 = z 15 .
Then (a3 , b 3 , c 3 ) is a solution to the equation
x 5 + y 5 = z 5.
So, if x 5 + y 5 = z 5 has no whole number solution, then neither does
x 15 + y 15 = z 15 .
Theorem
If Fermat’s Last Theorem holds for n = 4 and for all odd prime numbers n,
then Fermat’s Last Theorem holds for all n > 2.
Matt Valeriote (McMaster University)
Fermat’s Last Theorem
26 January, 2017
8 / 14
The case n = 4
Theorem (Fermat)
There are no positive integers a, b, and c such that
a4 + b 4 = c 4 .
Note
To prove this theorem, we instead prove the following stronger statement
from which the n = 4 case of Fermat’s Last Theorem will follow: there are
no positive integers x, y , and w such that
x 4 + y 4 = w 2.
(Since if a4 + b 4 = c 4 then x = a, y = b, w = c 2 would be a solution to
x 4 + y 4 = w 2 .)
Matt Valeriote (McMaster University)
Fermat’s Last Theorem
26 January, 2017
9 / 14
The equation x 4 + y 4 = w 2
Proof:
This proof makes use of a technique, called the method of infinite
descent, introduced by Fermat.
We start with the assumption that x, y , and w are positive integers
that satisfy the equation such that w is as small as possible amongst
all of the positive integer solutions to the equation.
We then produce new positive integers r , s, and t that are also a
solution to the equation, but with t < w .
This will contradict the minimality of w , and so we conclude that the
equation cannot have any positive integer solutions.
Matt Valeriote (McMaster University)
Fermat’s Last Theorem
26 January, 2017
10 / 14
Case 1: A common factor
Proof:
In this case, we assume that two of the numbers x, y , and w of our
solution have a common factor greater than 1.
We may assume that this common factor is some prime number p.
It follows that since p divides two of x, y , and w , then it divides all
three of them.
For example, if p divides x and y , then p will also divide x 4 + y 4 and
so p will divide w 2 .
Since p is prime, then p will actually divide w .
So, we may assume that p divides each of x, y , and w .
Then, p 4 divides x 4 + y 4 and so p 4 divides w 2 .
Since p is prime, then in fact, p 2 divides w .
Then r = x/p, s = y /p and t = w /p 2 are positive integers and a
solution to the equation (check), with t < w .
Matt Valeriote (McMaster University)
Fermat’s Last Theorem
26 January, 2017
11 / 14
Case 2: No common factors
Proof.
In the remaining case, we assume that no two of x, y , and w share a
common factor greater than 1.
Then x 2 , y 2 , and w do not share a common factor greater than 1.
Thus, since x 4 + y 4 = w 2 then (x 2 , y 2 , w ) is a primitive Pythagorean
triple.
From an earlier theorem, we know that there are relatively prime
natural numbers p and q with one odd, and the other even so that:
y 2 = 2pq,
x 2 = p2 − q2,
w = p2 + q2.
Then x 2 + q 2 = p 2 and so (x, q, p) is another primitive Pythagorean
triple (with p odd and q even).
Matt Valeriote (McMaster University)
Fermat’s Last Theorem
26 January, 2017
12 / 14
Case 2: No common factors
Proof.
Using primitive Pythagorean triples theorem, there are relatively prime
natural numbers m and n with one even and one odd so that:
q = 2mn,
x = m2 − n2 ,
p = m2 + n2 .
Using that y 2 = 2pq and that 2q and p are relatively prime, then
both 2q and p are squares. So p = t 2 for some positive integer t.
But, 2q = 4mn and since m and n are relatively prime, then m and n
are each squares.
Thus m = r 2 and n = s 2 for some positive integers r and s.
Using that m2 + n2 = p, we conclude that r 4 + s 4 = t 2 and so r , s,
and t is a solution to the equation.
Finally, we note that t ≤ p < p 2 + q 2 = w , a contradiction.
Matt Valeriote (McMaster University)
Fermat’s Last Theorem
26 January, 2017
13 / 14
Matt Valeriote (McMaster University)
Fermat’s Last Theorem
26 January, 2017
14 / 14