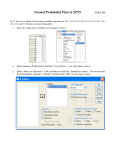
* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download PennState-jun06-unfolding
Plateau principle wikipedia , lookup
Computational phylogenetics wikipedia , lookup
Mathematical optimization wikipedia , lookup
Birthday problem wikipedia , lookup
Information theory wikipedia , lookup
Pattern recognition wikipedia , lookup
Inverse problem wikipedia , lookup
Computational electromagnetics wikipedia , lookup
Density matrix wikipedia , lookup
Least squares wikipedia , lookup
Data assimilation wikipedia , lookup
Mathematics of radio engineering wikipedia , lookup
Multidimensional empirical mode decomposition wikipedia , lookup
Non-negative matrix factorization wikipedia , lookup
Spectrum Reconstruction of Atmospheric Neutrinos with Unfolding Techniques Juande Zornoza UW Madison Introduction We will review different approaches for the reconstruction of the energy spectrum of atmospheric neutrinos: Blobel / Singular Value Decomposition actually, both methods are basically the same, with only differences in issues not directly related with the unfolding but with the regularization and so on Iterative Method based on Bayes’ theorem Spectrum reconstruction In principle, energy spectra can be obtained using the reconstructed energy of each event. However, this is not efficient in our case because of the combination of two factors: Fast decrease (power-law) of the flux. Large fluctuations in the energy deposition. For this reason, an alternative way has to be used: unfolding techniques. Spectrum unfolding •Quantity to obtain: y, which follows pdf→ftrue(y) •Measured quantity: b, which follows pdf→fmeas(b) •Both are related by the Fredholm integral equation of first kind: f meas (b) R(b | y) ftrue ( y )dy Matrix notation Ây b •The response matrix takes into account three factors: -Limited acceptance -Finite resolution -Transformation •The response matrix inversion gives useless solutions, due to the effect of statistical fluctuations Dealing with instabilities Regularization: Solution with minimum curvature Principle of maximum entropy Iterative procedure, leading asymptotically to the unfolded distribution Single Value Decomposition1 The response matrix is decomposed as: Aˆ USV T U, V: orthogonal matrices S: non-negative diagonal matrix (si, singular values) This can be also seen as a minimization problem: 2 ˆ Aij xi bi min i 1 j 1 nb nx Or, introducing the covariance matrix to take into account errors: ˆAx b T B 1 Aˆ x b min 1 A. Hoecker, Nucl. Inst. Meth. in Phys. Res. A 372:469 (1996) SVD: normalization Actually, it is convenient to normalize the unknowns Ây b w j y j / yini j nx A w j 1 ij j bi Aij contains the number of events, not the probability. Advantages: the vector w should be smooth, with small bin-to-bin variations avoid weighting too much the cases of 100% probability when only one event is in the bin SVD: Rescaling Rotation of matrices: B QRQ T 1 Aij Qim Amj ri m bi 1 Qimbm ri m allows to rewrite the system with a covariance matrix equal to I, more convenient to work with: ~T ~ ~ ~ ( Aw b ) ( Aw b ) min Regularization Several methods have been proposed for the regularization. The most common is to add a curvature term add a curvature term ~T ~ ~ ~ ( Aw b ) ( Aw b ) (Cw)T Cw min 1 1 C 0 1 2 1 0 1 1 1 2 0 1 0 1 1 Other option: principle of maximum entropy Regularization We have transformed the problem in the optimization of the value of , which tunes how much regularization we include: too large: physical information lost too small: statistical fluctuations spoil the result In order to optimize the value of : Evaluation using MC information Maximum curvature of the L-curve T Components of vector d U b L-curve Solution to the system Actually, the solution to the system with the curvature term can be expressed as a function of the solution without curvature: ny w' i 1 di f i vi si A ' AC 1 w ' Cw where d ( ) i si2 di 2 si 2 1 if s s i fi 2 2 si si / if si2 2 i (Tikhonov factors) Tikhonov factors The non-zero tau is equivalent to change di by 1 if si2 si2 fi 2 2 si si / if si2 And this allows to find a criteria to find a good tau fun0 fun1 fun2 Components of d k = sk2 Differences between SVD and Blobel More simplified implementation Possibility of different number of bins in y and b (non square A) Different curvature term Selection of optimum tau B-splines used in the standard Blobel implementation Bayesian Iterative 2 Method •If there are several causes (Ei) which can produce an effect Xj and we know the initial probability of the causes P(Ei), the conditional probability of the cause to be Ei when X is observed is: P( Ei | X j ) smearing matrix: MC P( X j | Ei ) P0 ( Ei ) P( X l 1 j | El ) P0 ( El ) prior guess: iterative approach •The expected number of events to be assigned to each of the nX causes is: nˆ ( Ei ) n( X j ) P( Ei | X j ) j 1 experimental data (simulated) •The dependence on the initial probability P0(Ei) can be overcome by an iterative process. nˆ ( Ei ) ˆ P( Ei ) nE nˆ( Ei ) i 1 2 G. D'Agostini NIM A362(1995) 487-498 Iterative algorithm 1. Choose the initial distribution P0(E). For instance, a good guess could be the atmospheric flux (without either prompt neutrinos or signal). 2. Calculate nˆ ( E ) and Pˆ ( E ). 3. Compare nˆ ( E ) to n0 ( E ). 4. Replace P0 ( E ) by Pˆ ( E ) and n0 ( E ) by nˆ ( E ). 5. Go to step 2. P(Xj|Ei) Smearing matrix (MC) no(E) Initial guess P(Ei|Xj) Reconsructed spectrum n(Ei) Po(E) n(Xj) Experimental data P(Ei) For IceCube Several parameters can be investigated: Number of channels Number of NPEs Reconstructed energy Neural network output… With IceCube, we will have much better statistics than with AMANDA But first, reconstruction with 9 strings will be the priority Remarks First, a good agreement between data and MC is necessary Different unfolding methods will be compared (several internal parameters to tune in each method) Several regularization techniques are also available in the literature Also an investigation on the best variable for unfolding has to be done Maybe several variables can be used in a multi-D analysis This is the end B-splines Spline: piecewise continuous and differentiable function that connects two neighbor points by a cubic polynomial: from H. Greene PhD. B-spline: spline functions can be expressed by a finite superposition of base functions (B-spilines). (first order) (higher orders) Maximum entropy In general, we want to minimise ln L S S can be the spikeness of the solution, or, the entropy of the system: S P ln P Probability of any event of being in bin i is fi/N. N i 1 i i Then, following the maximum entropy principle, we will minimize: ln L fi / N ln( fi / N ) i Useful for sharp gradients, i.e. when the solution it is not expected to be very smooth