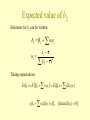Download The Simple Linear Regression Model Specification and Estimation

The Simple Linear Regression
Model Specification and
Estimation
Hill et al Chs 3 and 4
Expenditure by households of a
given income on food
Economic Model
• Assume that the relationship between
income and food expenditure is linear:
y  1  2 x
• But, expenditure is random:
E ( y | x)   y| x  1  2 x
• Known as the regression function.
Econometric model
Econometric model
• Combines the economic
model with assumptions
about the random nature
of the data.
• Dispersion.
• Independence of yi and
yj.
• xi is non-random.
Writing the model with an error
term
• An observation can be decomposed into a
systematic part:
– the mean;
• and a random part:
e  y  E ( y)  y  1  2 x
y  1  2 x  e
Properties of the error term
Assumptions of the simple linear
regression model
SR1
y  1   2 x  e
SR2.
E (e)  0  E ( y )  1   2 x
SR3.
var(e)   2  var( y )
SR4.
cov(ei , e j )  cov( yi , y j )  0
SR5. The variable x is not random and must take
at least two different values.
SR6. (optional) The values of e are normally
distributed about their mean
e ~ N (0,  2 )
The error term
• Unobservable (we never know E(y))
• Captures the effects of factors other than
income on food expenditure:
– Unobservered factors.
– Approximation error as a consequence of the
linear function.
– Random behaviour.
Fitting a line
The least squares principle
• Fitted regression and predicted values:
yˆt  b1  b2 xt
• Estimated residuals:
eˆt  yt  yˆt  yt  b1  b2 xt
• Sum of squared residuals:
 eˆ   ( y  yˆ )   eˆ
2
t
2
t
t
*2
t
  ( yt  yˆt* )2
The least squares estimators
T
S (1 , 2 )   ( yt  1  2 xt ) 2
t 1
S
 2T 1  2 yt  2 xt2  0
1
S
 2 xt22  2 xt yt  2 xt1  0
2
b2 
T  xt yt   xt  yt
T  xt2    xt 
b1  y  b2 x
2
Least Squares Estimates
• When data are used with the estimators, we obtain
estimates.
• Estimates are a function of the yt which are
random.
• Estimates are also random, a different sample with
give different estimates.
• Two questions:
– What are the means, variances and distributions of the
estimates.
– How does the least squares rule compare with other
rules.
Expected value of b2
Estimator for b2 can be written:
b2  2   wt et
xt  x
wt 
2
(
x

x
)
 t
Taking expectations:
E (b2 )  E  2   wt et   E (2 )   E ( wt et )
 2   wt E (et )  2
[since E (et )  0]
Variances and covariances
2




x
2
x

t
2
2
var(b1 )   
, var(b2 ) 
,cov(b1, b2 )   
2
2
2
T
(
x

x
)
(
x

x
)
(
x

x
)
  t

  t

 t
2

1. The variance of the random error term, , appears in each of the
2.
3.
4.
5.
expressions.
The sum of squares of the values of x about their sample mean,
( xt  x ) 2 , appears in each of the variances and in the
covariance.
The larger the sample size T the smaller the variances and
covariance of the least squares estimators; it is better to have more
sample data than less.
The term x2 appears in var(b1).
The sample mean of the x-values appears in cov(b1,b2).

Comparing the least squares
estimators with other estimators
Gauss-Markov Theorem: Under the assumptions SR1-SR5 of the
linear regression model the estimators b1 and b2 have the smallest
variance of all linear and unbiased estimators of 1 and 2. They are
the Best Linear Unbiased Estimators (BLUE) of 1 and 2
The probability distribution of
least squares estimators
• Random errors are normally distributed:
– estimators are a linear function of the errors,
hence they a normal too.
• Random errors not normal but sample is
large:
– asymptotic theory shows the estimates are
approximately normal.
Estimating the variance of the
error term
var(et )    E[et  E (et )]  E (e )
2
2
ˆ 2 
2
t
2
e
t
T
et  yt  1  2 xt
eˆt  yt  b1  b2 xt
ˆ 2 
2
ˆ
e
t
T 2
Estimating the variances and
covariances of the LS estimators
2


x

t
2
ˆ b1 )  ˆ 
var(
,
2
 T  ( xt  x ) 
ˆ 2
ˆ b2 ) 
var(
,
2
 ( xt  x )


x
ˆ b1 , b2 )  ˆ 
cov(
2
  ( xt  x ) 
2
ˆ b1 )
se(b1 )  var(
ˆ b2 )
se(b2 )  var(