Download MULTICAST RECIPIENT MAXIMIZATION PROBLEM IN 802 16

M ULTICAST R ECIPIENT M AXIMIZATION
802 16 W I MAX R ELAY
P ROBLEM IN 802.16
N ETWORKS

郭文興, 32 years old
郭文興, 32 years old

Bachelor, National Taiwan University (1998~2002)

PhD in EE, National Taiwan University
(2002~2008) Advisor: Wanjiun Liao

Assistant Professor, Department of EE, Yuan Ze
University (2008~)
O UTLINE

Multicast Recipient Maximization Problem

Related Works and Similar Problems

Proposed Solution
Proposed Solution

Numerical Results

Another Problem BMR
Another Problem: BMR

Proposed Solution

Numerical Results

Conclusions
O UTLINE

Multicast Recipient Maximization Problem

Related Works and Similar Problems

Proposed Solution
Proposed Solution

Simulation Results

Another Problem BMR
Another Problem: BMR

Proposed Solution

Simulation Results

Conclusions
802 16 W I MAX
802.16

IEEE 802.16 (WiMAX) is an emerging last mile IEEE
802.16 (WiMAX) is an emerging last mile
technology for broadband wireless access.

Compared with 3G cellular networks and IEEE Compared with 3G cellular networks and IEEE
802.11 Wi‐Fi, it has better coverage and throughput.

A typical IEEE 802.16 WiMAX network comprises a base station (BS) and multiple subscriber stations (SSs)
802 16 W I MAX
802.16

IEEE 802.16j standard introduces a new type of IEEE
802.16j standard introduces a new type of
infrastructure nodes called relay stations (RSs). 
Specifically, RSs forward data, both upward and Specifically RSs forward data both upward and
downward, over the wireless medium between the BS and the SSs to increase the system capacity and throughput.
802 16 W I MAX
802.16
802 16 W I MAX
802.16
M ULTICAST R ECIPIENT
M AXIMIZATION P ROBLEM

WiMAX technology is an efficient platform for multicast services. 
Wireless resource is relatively scarce; hence, the resource available for each wireless service is inevitably
limited.

With the given budget, a BS should serve as many recipients (i e SSs)
recipients (i.e., SSs). 
When a network only consists of a BS and SSs ‐> tuning the allocated resource of the BS. 
Relay Networks ‐>The problem becomes much difficult because resource must be allocated between the BS and the RSs.
O UTLINE

Multicast Recipient Maximization Problem

Related Works and Similar Problems

Proposed Solution
Proposed Solution

Simulation Results

Another Problem BMR
Another Problem: BMR

Proposed Solution

Simulation Results

Conclusions
R ELATED W ORKS

In [5], a reliable multicast scheme uses Code In
[5], a reliable multicast scheme uses Code
Division Multiple Access (CDMA) codes in WiMAX networks

[6] proposes a two‐level superposition coded multicast scheme (2‐level SCM) to improve the channel efficiency.

[11] considers, two kinds of nodes, (i.e., relay nodes and receiving nodes, ) but with fixed allocated energy.
S IMILAR P ROBLEM :
M INIMUM -E NERGY
M ULTICAST (MEM)

Given the channel condition of each node, the Given
the channel condition of each node, the
MEM problem finds the multicast tree that minimizes the total energy required to deliver the stream to a given set of subscribers.
h
i
f b ib
S IMILAR P ROBLEM :
M INIMUM -E NERGY
M ULTICAST (MEM)

Although MEM appears to be similar to our Although
MEM appears to be similar to our
Multicast Recipient Maximization (MRM) scheme, they are substantially different:
~
MEM assumes that each intermediate node can forward data. ~
MEM minimizes the resource required to serve subscribers. ~
Each node is assumed to separately receive a copy from its sender in MEM. O UTLINE

Multicast Recipient Maximization Problem

Related Works and Similar Problems

Proposed Solution
Proposed Solution

Simulation Results

Another Problem BMR
Another Problem: BMR

Proposed Solution

Simulation Results

Conclusions
N OTATIONS
D EFINITION OF MRM

The routing of each SS is assumed to be decided beforehand

It is impractical that the whole multicast tree can be whole multicast tree can be
dynamically formed and adjusted as any recipient changes its channel condition. s 0 ,1
sM,NM
s0,2
s0, N0
s1 ,1
s0,3
s1,2
s1N
, 1
s2,1 s
2,2
s2,N2
sM,2
sM ,1
D EFINITION OF MRM

Given the channel quality , RS Given
the channel quality R = [R 0 , R1 , R 2 ,,...,, R M ] , RS
r
I = [i0 , i1 ,..., iM ]
positions , and budget , find a Γ = [ n , n ,..., n ]
resource allocation that maximizes the total number of served SSs h
l
b
f
d SS
∑ D (n ) ⋅ (U (n ) − U (i ))
(i.e., ), subject to the total M
consumed resource m∑=0 (r(m, n ) − r(m,0) ) ≤ rbudget
g
budget
0
1
M
M
m =0
m
0
m
m
0
m
m
im ≤ n
⎧1
Dm ( n ) = ⎨
⎩0 otherwise
m=0
⎧⎪n − max m′
U m (n) = ⎨ im′ ≤n
⎪⎩n + U 0 (im ) otherwise
D IFFICULTY OF MRM

MRM is NP‐complete
MRM is NP
complete
~
It is NP‐hard because it can be reduced from a famous problem called integral knapsack.
famous problem called integral knapsack.
~
It is NP because the performance of a single instance can be verified in polynomial time.
p y
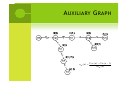
A UXILIARY G RAPH

For each node, the total distance (i.e. the sum of ,
(
weight of edges) to the root is equal to the number of resource it requires.

MRM involves finding a spanning tree rooted at BS i l
fi di
i
d
S
that maximizes the number of SSs covered, subject to the constraint that the total length of the tree is not greater than the resource budget.
t th th
b d t
BS ( RS0 )
Δr0 (1)
ss
Δr0(2)
r( 0,1)
r(0, 2)
r( 0 , 3 )
r(1 ,1 )
r(1, 2 )
ss
RS2
RS 1
Δr0 (3)
Δr0 (4)
Δr1 (1)
ss RSM
ss
ss
ss
ss
ss
Δr1 (2)
ss
ss
ss1N1
ss
A UXILIARY G RAPH
2
1
0.4
0. 1
u m (n) =
U m ( n ) − U m ( n − 1)
Δ rm ( n )
E NVELOPE F UNCTION
*
′
U
(
n
)
−
U
*
m
m ( n − 1)
u m ( n) =
max
S ( m′.n′ ) ∈ST(m,
(m n) r( m ′, n ′) − r( m , n −1)
*
*
*
Um
(n) = U m
( n − 1) + u m
( n ) Δrm ( n )
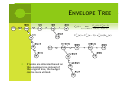
E NVELOPE T REE
*
um
( n) =
*
U m (n′) − U m
(n − 1)
S ( m′.n′ ) ∈ST(m,n) r( m ′, n ′) − r( m, n −1)
max
*
*
*
Um
(n) = U m
(n − 1) + u m
( n)Δrm (n)

If nodes are allocated based on the envelope tree instead of g
,
g
the original tree, the budget can be more utilized.
P ROPOSED DSS S CHEME
P ROPOSED DSS S CHEME
P ERFORMANCE A NALYSIS

DSS has polynomial‐time
DSS has polynomial
time complexity.
complexity.

*
∀ m, n, .
Um
(n) ≥ U m (n)

∀ S ( m ′, n ′ ) ∈ ST ( m , n )
u m* ( n ) ≥ u m* ′ ( n ′)
, . (i.e., nodes farther from U m* ( n)
the BS have smaller . The envelope tree if concave)
concave) P ERFORMANCE A NALYSIS

Γ op _ R
: the optimal solution to the envelop tree
: the optimal solution to the envelop tree

Γ op
: the optimal solution to the original tree


Γ DSS = Γ op _ R
P MRM ( Γ
op
) − P MRM ( Γ
≤ P R − MRM ( Γ
= P R − MRM ( Γ
= max {U
∀ m ,n
*
m
op _ r
DSS
DSS
)
) − P MRM ( Γ
) − P MRM ( Γ
(n ) − U
m
( n )}
)
DSS
DSS
)
O UTLINE

Multicast Recipient Maximization Problem

Related Works and Similar Problems

Proposed Solution
Proposed Solution

Simulation Results

Another Problem BMR
Another Problem: BMR

Proposed Solution

Simulation Results

Conclusions
S IMULATION S ETTINGS

1
The required resource is represented as d .
The required resource is represented as .
a
~
d is the distance between the sender and receiver ~
a is the channel attenuation factor that is usually between 2 and 4. S IMULATION I

In the first simulation, M
In
the first simulation, M and N
and N are fixed at 5 and are fixed at 5 and
100 respectively. 
Since the network topologies are generated Since the network topologies are generated
randomly, we conduct 100 runs for each setting.
S IMULATION I
S IMULTAION I

The trends of both figures are very similar, The
trends of both figures are very similar,
meaning that DSS provides same satisfying performance under different radio conditions. 
Given different budgets, DSS always outperforms GD. S IMULATION II

rbudget = 20000
20000

a=2

We tune the value of N from 100 to 1000 to observe the impact of recipient number on the performance.
performance

Again, each point on the curves represents the average of 100 simulation runs.
f 100 i l ti
S IMULATION II
S IMULATION II

The number of served recipients is linearly The
number of served recipients is linearly
proportional to the node number. 
This is because more SSs result in higher density. This is because more SSs result in higher density
Given the same amount of allocated resource, more SSs would be served.

As N increases, the performance of DSS always stays close to that of OP, while the difference between OP and GD increases. O UTLINE

Multicast Recipient Maximization Problem

Related Works and Similar Problems

Proposed Solution
Proposed Solution

Simulation Results

Another Problem BMR
Another Problem: BMR

Proposed Solution

Simulation Results

Conclusions
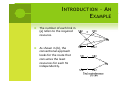
I NTRODUCTION – A N
E XAMPLE

The number of each link in (a) refers to the required resource. 
As shown in (b), the conventional approach
conventional approach looks for the route that consumes the least resources for each SS independently.
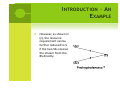
I NTRODUCTION – A N
E XAMPLE

However, as shown in (c), the resource requirement can be requirement can be
further reduced to 5 if the two SSs receive the stream from the h
f
h
BS directly. S YSTEM M ODEL AND
P ROBLEM S PECIFICATION

RS0 : the BS

RSy , : the yth
RS
1≤ y ≤ Y

SS n , : the nth SS
1≤ n ≤ N

Y, N: the number of RS and SS respectively

rn , y
: the required resource for multicast from y to n

ry
: the required resource of RSy

ra y
: the resource allocated to RS y

RA = [ra 0 , ra1 ,...raY ] : the resource allocation

rtotal
: the total resource budget
S YSTEM M ODEL AND
P ROBLEM S PECIFICATION
ry
r1 r 2
RS 1
rY
RS y
RS2
RS Y
rn , 0
rn ,1 rn, 2
SS1
SS2
rn , y rn,Y
SS n
rN ,Y
SSN
S YSTEM M ODEL AND
P ROBLEM S PECIFICATION

Find that maximizes RA = [ra 0 , ra1 ,...raY ]
N
Y
n =1
y =0
∑ min((1, ∑ U (ra y − rn, y )U (ra 0 − ry ))

Subject to
Y
~
∑ ra y ≤ rtotal
y =0
~
0 ≤ ra y ≤ rtotal
O UTLINE

Multicast Recipient Maximization Problem

Related Works and Similar Problems

Proposed Solution
Proposed Solution

Simulation Results

Another Problem BMR
Another Problem: BMR

Proposed Solution

Simulation Results

Conclusions
for n=1 to N, rn,0 is put in a queue q;
q is sorted in decreasing order of r ;
ra0DRA ← rtotal ;
for y=1 to Y, ra yDRA ← 0 ;
RAmax ← RADRA ;
do
q′ ← q ;
DRA
are popped from q′ ;
all elements larger than ra0
do
for y=1 to Y,
RAtemp ← RADRA ; Δr ← r0temp − q′[0] ;
r0temp ← q ′[0] ; r ytemp ← r yanswer + Δ r ;
temp
max
if P ( RA ) > P ( RA ) then
RAmax ← RAtemp ;
end if;
end for;
q ′[0] is popped from the queue;
ratemp
loop until ( q′[0] < 1≤ y≤Ymax
) or ( q′ is empty);
y
, ra
>0
DRA
← RAmax ;
if RA max ≠ RA DRA then RA
else
l exit
it do;
d
end if;
loop;
return RADRA ;
n, 0
temp
y
P ERFORMANCE E VALUATION –
S IMULATION S ETTING



The coordinate of the BS is
The coordinate of the BS is set as (0,0). In each run, the positions of ,
p
all SSs are randomly distributed in a circular area whose center and radius are whose center and radius are
(0,0) and 100 respectively. All the RSs are placed All
the RSs are placed
randomly in circular region whose radius ranges from 40 to 60 such that each RS is
40 to 60 such that each RS is located between the BS and some SSs
Range of SSs
Range of RSs
0
10
60
40
RS (0,0)
O UTLINE

Multicast Recipient Maximization Problem

Related Works and Similar Problems

Proposed Solution
Proposed Solution

Simulation Results

Another Problem BMR
Another Problem: BMR

Proposed Solution

Simulation Results

Conclusions
S IMULATION I

In the first simulation, we compare the In
the first simulation, we compare the
performance of the allocations of the three schemes under different resource budgets. 
The value of N and Y are fixed at 100 and 5
respectively, while the value of is tuned in the range 0 to 1,000,000. 
Each point is averaged over 100 random node placements.
S IMULATION I
Available Resouce v.s. Served SSs
(Y=5, N=100, a=2)
Number of Serrved SSss
100
80
60
ra^BS
40
ra^DRA
20
ra^fixed
0
0
2000
4000
6000
r_total
8000
10000
S IMULATION I

More SSs are served as the budget increases
More SSs are served as the budget increases

ra^DRA achieves a better performance than ra
BS and ra
fixed, indicating that the ra^BS
and ra^fixed
indicating that the
participation of RSs allows more SSs to be served, and thus improves resource utilization. 
Although RSs are also used in rs^fixed, it does not yield an obvious performance gain over rs^BS.
S IMULATION II
rtotal

Next, we fix the value of N, and at 100 and Next,
we fix the value of N, and
at 100 and
500,000 respectively, and tune the number of RSs (i.e., Y) from 0 to 5 to observe the impact of RS density on performance. RS d i
f

Again, each point is averaged over 100 runs. S IMULATION II
v s Served SSs
Number of RSs v.s.
(N=100, a=3, r_total=500000)
Numberr of Serveed SSs
100
80
60
ra^BS
40
ra^DRA
20
ra^fixed
ra
fixed
0
0
1
2
Y
3
4
5
S IMULATION II

Given the same budget, the performance of Given
the same budget, the performance of
ra^DRA improves as Y grows, while that of ra^BS
remains unchanged because RSs are not used. 
Although RSs also relay the stream for SSs in ra^fixed, a significant increasing trend and performance gain over are not observed because finding the minimal route independently does not achieve high resource utilization in
not achieve high resource utilization in multicast.. O UTLINE

Multicast Recipient Maximization Problem

Related Works and Similar Problems

Proposed Solution
Proposed Solution

Simulation Results

Another Problem BMR
Another Problem: BMR

Proposed Solution

Simulation Results

Conclusions
C ONCLUSION

We study the multicast maximization problem in y
p
802.16j WiMAX relay networks. 
MEM aims to maximize the number of recipients in a fixed network topology fi d
k
l

We prove that the maximization has the performance very approximate to the optimum
very approximate to the optimum

MRM aims to maximize the number of recipients in a dynamic network topology
dynamic network topology

The simulation results show that the performance is satisfying
R EFERENCE

Wen Hsing Kuo and Jeng
Wen‐Hsing
Jeng‐Farn
Farn Lee, Lee, “Multicast
Multicast Recipient Maximization in IEEE 802.16j WiMAX Relay Networks,” IEEE Transactions on Vehicular Technology, vol. 1, pp.335‐343, Jan. 2010.
T h l
l 1
335 343 J 2010

Wen‐Hsing Kuo and Jeng‐Farn Lee, "Multicast Routing Scheme for Recipient Maximization in Wireless Relay Networks," IEEE Transactions on Vehicular Technology, Vol. 8, Issue 19, pp.4002‐
Vehicular Technology, Vol. 8, Issue 19, pp.4002
4011, Oct. 2010.