* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download The HR Diagram Interpreted (PowerPoint version)
Constellation wikipedia , lookup
Corona Borealis wikipedia , lookup
Canis Minor wikipedia , lookup
Chinese astronomy wikipedia , lookup
Theoretical astronomy wikipedia , lookup
History of Solar System formation and evolution hypotheses wikipedia , lookup
Tropical year wikipedia , lookup
Astronomical unit wikipedia , lookup
Geocentric model wikipedia , lookup
Cassiopeia (constellation) wikipedia , lookup
Rare Earth hypothesis wikipedia , lookup
Cygnus (constellation) wikipedia , lookup
Formation and evolution of the Solar System wikipedia , lookup
International Ultraviolet Explorer wikipedia , lookup
History of astronomy wikipedia , lookup
Perseus (constellation) wikipedia , lookup
H II region wikipedia , lookup
Dialogue Concerning the Two Chief World Systems wikipedia , lookup
Stellar classification wikipedia , lookup
Aquarius (constellation) wikipedia , lookup
Planetary habitability wikipedia , lookup
Canis Major wikipedia , lookup
Star formation wikipedia , lookup
Observational astronomy wikipedia , lookup
Hebrew astronomy wikipedia , lookup
Stellar kinematics wikipedia , lookup
Stellar evolution wikipedia , lookup
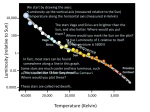
The HR Diagram Interpreted: Properties of Stars Why These Names? “Main Sequence” is a ‘no-brainer.’ But why Red Why White Giant? Dwarf? Remember the Radiation Laws [See ASTR 101] Consider two glowing objects of exactly the same size. The luminosity flowing out depends on the 4th power of the temperature (= T4), with T measured upwards from ‘absolute zero.’ So one object twice as hot as another identical one emits 24 = 2x2x2x2 = 16 times as much energy. In Other Words... All other things being equal, hot bodies shine more brightly than cooler bodies. But Can a Cool Body Outshine a Hot Body? Yes, it can – but only if it has a huge surface area, every square centimeter of which will contribute a little bit. Consider Betelgeuse The Sun, a G star, is about twice the temperature of Betelgeuse, an M star. If they were the same size, the Sun would be 16x as bright! But Betelgeuse is 10,000 times as bright overall. This tells us that it must have 160,000 times as much surface area! This means that it must be 400x as big across. In other words, if we replaced the Sun with Betelgeuse, the Earth would be inside it! It is truly a red (cool) giant. The Size of Betelgeuse Another Giant, Drawn to Scale Notice that we do not measure these sizes directly: essentially all the stars appear as unresolved points of light. But knowing their intrinsic luminosities (how much total energy they emit) and their surface temperatures tells us their sizes right away! (The study of eclipsing binary stars allows us to check and confirm these determinations independently.) Comparing Sizes in Astronomy From Small to Huge Visit http://apod.nasa.gov/apod/ap130606.html from the “Astronomy Picture of the Day” website Note also the various colours, indicative of different temperatures. [This montage starts with the moon and planets, the visible colours of which are determined by reflected sunlight: they are so cool that they ‘glow’ in the infrared. The beautiful blue planet Earth is not at a temperature of 20,000 K!] So Much For the Red Giants: We Can Turn this Argument Around Let’s imagine a very hot object that is extremely faint. How can this be? Answer: it must be very small, with a limited surface area to radiate its heat and light. Reconsider the HR Diagram Notice the hot but faint ‘white dwarfs’ - twice as hot as the Sun, but less than 1% as bright! One Nearby Example: the Companion of Sirius As hot as Sirius itself, but very faint. So it must be small: a “white dwarf” Indeed, ‘Sirius B’ is Earth-sized! You may say “so what?” – perhaps you expected there to be very small stars. But further analysis reveals something amazing. This is a True Binary Star Sirius and its companion orbit each other Notice how they orbit their common center of mass, once every ~50 years. [The light of Sirius A has been suppressed in this series of images so that B shows up clearly] When We Apply Newton’s Laws… …we discover that Sirius B is just as massive as the sun. But we know it is somewhat smaller than the Earth (to explain its limited brightness) A simple calculation then reveals that ‘Sirius B’ is one million times as dense as water - a tonne per cubic cm There is nothing on Earth like this. This is ‘new physics.’ Sizes Shown Schematically (but not to correct scale: the ‘supergiants’ are really huge!) Some Specific Stars with radii shown (compared to the Sun) The Ranges are Worth Noting Stars range, roughly, from 3000 K (cool, red) to 30,000 K (hot, giving off lots of ultraviolet light!) in surface temperature from 1% of the sun’s diameter to 1000 times its size from a thousandth of the sun’s brightness to a million times as bright A Peek Forward in Time: Our Fate As noted, if Betelgeuse were put down where the sun is, the Earth would be inside it. As we will come to learn in this course: The sun’s eventual fate is to pass through a stage in which it will swell to red giant proportions But it will eventually end up as a white dwarf! Q: What is an ‘Average’ Star? We have to be careful about what we mean by “average.” Suppose you earned these first-year marks, in ten courses: 50, 50, 50, 50, 50, 50, 50, 60, 75, 100 Is the “average” mark 75 because it is exactly in the middle of the range? I think not! Is the Sun an ‘Average’ Star? It is (roughly) in the middle of the range, so it is certainly not unusual. But is it average? Analogy: is a human being an average-sized living creature? We are in the ‘mid-range’, between blue whales and bacteria, giraffes and mice,… But there are many more bacteria and ants than people and whales! Relative Numbers of Stars How many stars are there of various kinds? (The brightest supergiant stars, for example, catch the eye. But are they rare, or commonplace?) Remember my informal‘law of nature’: for every big thing, there are lots of little things. The same sort of ‘law’ applies in astronomy: super-bright stars are rare, but there are lots of little faint ones. The HR Diagram with Populations For every bright blue “O” star, there are more than a million faint red dwarfs low on the main sequence. So: The Truly ‘Average’ Star … is an undistinguished low-luminosity star, fainter and cooler than the sun. The Sun is ‘mid-range’ in its properties, and technically “above average” in size and mass – but it’s not a superstar. The Most Influential Stars The stars that we notice in the night sky, however, are the biggest, brightest ones – not at all ‘average!’ As we will learn later, such stars have also had the greatest role to play in the history of our galaxy and the universe, indeed making our very existence possible! So such stars are not only prominent but also influential.