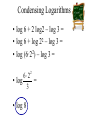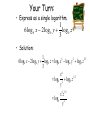Download log 2 - peacock

Algebra 2
Properties of Logarithms
Lesson 7-4
Goals
Goal
• To use the properties of
logarithms.
Rubric
Level 1 – Know the goals.
Level 2 – Fully understand the
goals.
Level 3 – Use the goals to
solve simple problems.
Level 4 – Use the goals to
solve more advanced problems.
Level 5 – Adapts and applies
the goals to different and more
complex problems.
Vocabulary
• Change of Base Formula
Essential Question
Big Idea: Modeling
•
How are the properties of logarithms similar to
the properties of exponents?
History of Logarithms
John Napier, a 16th Century Scottish
scholar, contributed a host of mathematical
discoveries.
He is credited with creating the first
computing machine, logarithms and was
the first to describe the systematic use of
the decimal point.
Napier lived during a time when
revolutionary astronomical discoveries
were being made.
But 16th century arithmetic was barely up
to the task and Napier became interested
in this problem.
John Napier (1550 – 1617)
Napier’s Bones
In 1617, the last year of his life, Napier
invented a tool called “Napier's Bones”
which reduces the effort it takes to
multiply numbers.
“Seeing there is nothing that is so troublesome to mathematical
practice, nor that doth more molest and hinder calculators, than the
multiplications, divisions... I began therefore to consider in my mind
by what certain and ready art I might remove those hindrances.”
Logarithms Appear
The first definition of the logarithm was constructed by
Napier and popularized by a pamphlet published in 1614,
two years before his death. His goal: reduce multiplication,
division, and root extraction to simple addition and
subtraction.
Napier defined the "logarithm" L of a number N by:
N==107(1-10(-7))L
This is written as NapLog(N) = L or NL(N) = L
While Napier's definition for logarithms is different from the
modern one, it transforms multiplication and division into
addition and subtraction in exactly the same way.
Properties of Logarithms
Because logarithms are exponents, you can derive the
properties of logarithms from the properties of
exponents
Product Property
Remember that to multiply powers
with the same base, you add
exponents.
Product Property
The property in the previous slide can be used in reverse to
write a sum of logarithms (exponents) as a single logarithm,
which can often be simplified.
Helpful Hint
Think: log j + log a + log m = log jam
Example:
Express log64 + log69 as a single logarithm. Simplify.
log64 + log69
log6 (4  9)
To add the logarithms, multiply the numbers.
log6 36
Simplify.
2
Think: 6? = 36.
Your Turn:
Express as a single logarithm. Simplify, if possible.
log5625 + log525
log5 (625 • 25)
To add the logarithms, multiply the
numbers.
log5 15,625
Simplify.
6
Think: 5? = 15625
Your Turn:
Express as a single logarithm. Simplify, if possible.
log 1 27 + log
3
log 1 ( 27 •
3
log 1 3
1
9
1
3
)
1
9
To add the logarithms, multiply the
numbers.
Simplify.
3
–1
Think: 1 ? = 3
3
Quotient Property
Remember that to divide powers
with the same base, you subtract
exponents
Because logarithms are exponents, subtracting logarithms with the same
base is the same as finding the logarithms of the quotient with that base.
Quotient Property
The property on the last slide can also be used in
reverse.
Caution
Just as a5b3 cannot be simplified, logarithms must have the
same base to be simplified.
Example:
Express log5100 – log54 as a single logarithm. Simplify, if possible.
log5100 – log54
log5(100 ÷ 4)
To subtract the logarithms, divide the
numbers.
log525
Simplify.
2
Think: 5? = 25.
Your Turn:
Express log749 – log77 as a single logarithm. Simplify, if possible.
log749 – log77
log7(49 ÷ 7)
To subtract the logarithms, divide the
numbers
log77
Simplify.
1
Think: 7? = 7.
Power Property
Because you can multiply logarithms, you can also take
powers of logarithms.
Example:
Express as a product. Simplify, if possible.
A. log2326
B. log8420
20log84
6log232
6(5) = 30
Because
25 = 32,
log232 = 5.
20( 2 ) =
3
40
3
Because
2
3
8 = 4,
log84 = 2 .
3
Your Turn:
Express as a product. Simplify, if possibly.
a. log104
b. log5252
4log10
4(1) = 4
2log525
Because
101 = 10,
log 10 = 1.
2(2) = 4
Because
52 = 25,
log525 = 2.
Your Turn:
Express as a product. Simplify, if possibly.
c. log2 (
5log2 (
1 5
)
2
1
2
5(–1) = –5
)
Because
1
2–1 = 2 ,
log2 1 = –1.
2
Summary
Properties of Logs
Product Rule log a xy  log a x  log a y.
Quotient Rule log a xy  log a x  log a y.
r
log
x
 r log a x.
Power Rule
a
• The properties of logarithms are useful for rewriting logarithmic expressions in
forms that simplify the operations of algebra.
• This is because the properties convert more complicated products, quotients, and
exponential forms into simpler sums, differences, and products.
• This is called expanding a logarithmic expression.
• The procedure above can be reversed to produce a single logarithmic expression.
• This is called condensing a logarithmic expression.
Examples:
• Expand:
• log 5mn =
• log 5 + log m + log n
• Expand:
• log58x3 =
• log58 + 3·log5x
Your Turn:
Expand:
Express as a
Sum and
Difference of
Logarithms
7x
• log2 =
y
3
• log27x3 - log2y =
• log27 + log2x3 – log2y =
• log27 + 3·log2x – log2y
Condense - Express as a Single
Logarithm
Example: Write the following as the logarithm
of a single expression.
5log6(x  3)  [2log6(x  4)  3log 6 x]
5log6(x  3)  [2log6(x  4)  3log 6 x]
 log 6(x  3)5  [log 6(x  4) 2  log 6 x3]
Power Rule
 log 6(x  3)5  [log 6(x  4) 2  x3]
Product Rule
 (x  3)5 
 log 6 
2 3
(
x

4)
x 

Quotient Rule
Condensing Logarithms
• log 6 + 2 log2 – log 3 =
• log 6 + log 22 – log 3 =
• log (6·22) – log 3 =
62
• log
=
3
2
• log 8
Your Turn:
• Condense:
• log57 + 3·log5t =
• log57t3
• Condense:
• 3log2x – (log24 + log2y)=
3
x
• log2
4y
Your Turn:
• Express in terms of sums and
differences of logarithms.
3
wy
log a 2
z
4
• Solution:
3
4
w y
3 4
2
log a 2  log a ( w y )  log a z
z
 log a w3  log a y 4  log a z 2
 3log a w  4log a y  2log a z
Your Turn:
• Express as a single logarithm.
1
6log b x  2log b y  log b z
3
• Solution:
1
6logb x  2logb y  logb z  logb x 6  logb y 2  logb z1/3
3
x6
1/3
 logb 2  log b z
y
x 6 z1/3
x6 3 z
 logb 2 , or log b 2
y
y
Another Type of Problem
• If loga3 = x and loga4 = y, express each log
expression in terms of x and y.
1. loga12
– Loga(3•4) = loga3 + loga4 = x+y
2. Log34
– Log34 = loga4/loga3 = y/x
Inverse Properties
Exponential and logarithmic operations undo each other since
they are inverse operations.
Example:
Simplify each expression.
a. log3311
b. log381
log3311
log33  3  3  3
11
log33
4
4
c. 5log510
5log510
10
Your Turn:
a. Simplify log100.9
b. Simplify 2log2(8x)
log 100.9
2log2(8x)
0.9
8x
Change of Base
Most calculators calculate logarithms only in base 10 or base e.
You can change a logarithm in one base to a logarithm in
another base with the following formula.
Change to base 10: logb x 
log x
log b
Example:
Evaluate log328.
Method 1 Change to base 10
log328 =
log8
log32
≈
0.903
1.51
≈ 0.6
Use a calculator.
Divide.
Example: Continued
Evaluate log328.
Method 2 Change to base 2, because both 32 and 8 are powers
of 2.
log328 = log28 = 3
5
log232
= 0.6
Use a calculator.
Your Turn:
Evaluate log927.
Method 1 Change to base 10.
log27
log9
log927 =
≈
1.431
0.954
≈ 1.5
Use a calculator.
Divide.
Your Turn: Continued
Evaluate log927.
Method 2 Change to base 3, because both 27 and 9 are powers
of 3.
log927 =
3
log327
=
2
log39
= 1.5
Use a calculator.
Your Turn:
Evaluate log816.
Method 1 Change to base 10.
log16
log8
Log816 =
≈
1.204
0.903
≈ 1.3
Use a calculator.
Divide.
Your Turn: Continued
Evaluate log816.
Method 2 Change to base 4, because both 16 and 8 are powers
of 2.
log816 =
= 1.3
2
log416
=
1.5
log48
Use a calculator.
Essential Question
Big Idea: Modeling
•
How are the properties of logarithms similar to
the properties of exponents?
•
The properties of logarithms are derived from the
properties of exponents. Use the Product,
Quotient, and Power Properties to condense or
expand logarithms.
Essential Question
Big Idea: Modeling
•
Why is the change of base formula useful?
•
The Change of Base Formula allows you to write a
logarithmic expression in one base as an equivalent
logarithmic expression in another base (usually base 10).
Use the Change of Base Formula to evaluate logarithmic
expressions with a calculator.
Assignment
• Section 7-4, Pg 495 – 497; #1 – 8 all, 10 –
22 even, 26 – 38 even, 42.