Download Informed search algorithms

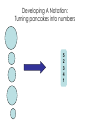
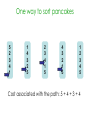
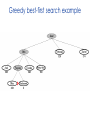
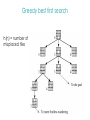
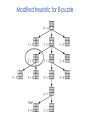
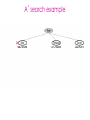
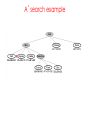
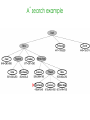
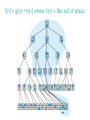
Lecture 3
Jan 28, 2014
• Chapter 3 (BFS, iterative deepening)
• Chapter 4
• Informed search
Outline
• Greedy search
– greedy depth-first search
– best-first search
• A* search
• Properties of Heuristics
– Admissibility, monotonicity, etc.
• Memoized search (a.k.a. dynamic
programming)
• Automatic generation of heuristics
Heuristic - estimate of distance to goal
Uninformed search - children (successors) of a
node were considered in arbitrary order.
Heuristic search – successors are compared to
determine which one is more likely to lead to a
solution.
Search cost – if the edges are weighted,
moving from p to q incurs a cost of w(p, q).
Sliding piece puzzle (8-puzzle)
Cost of each sliding
move = 1
Heuristic: number of misplaced tiles
Our search heuristic moves as quickly toward
the goal as possible.
We will select the move of moving the blank to
the left in Figure 4.1.
Extending this analysis will lead us to move the
blank up next and then to the right, arriving at
the goal configuration after three moves.
Maze search problem
Goal: Find a path from s to g.
s
g
Heuristic: distance from node n to g disregarding the
barriers.
Does not work well in this example.
Greedy depth-first search algorithm (hill-climbing)
Romania with step costs in km
Pancake sorting problem
• Several pancakes are on a plate.
• Goal is to sort them (so that the largest is at
the bottom).
• Operation: pick the top k pancakes (using a
spatula) and flip them over.
• Cost: k units for flipping k pancakes at a
time.
Developing A Notation:
Turning pancakes into numbers
5
2
3
4
1
What is the cost to sort this stack?
5
2
3
4
1
One way to sort pancakes
5
2
3
4
1
1
4
3
2
5
2
3
4
1
5
4
3
2
1
5
1
2
3
4
5
Cost associated with the path: 5 + 4 + 3 + 4
H(n) for some problems
• 8-puzzle (sliding piece puzzle)
– W(n): number of misplaced tiles
– Manhatten distance
• Pancake sorting problem – what is a good H?
• Unconditional distance to destination in search
– Euclidean or Manhattan distance
Best-first search
• Idea: use an evaluation function f(n) for each
node n
– estimate of "desirability
– Expand most desirable unexpanded node (which
need not be a child of the node expanded in the
previous step)
Difference between hill-climbing
and greedy Best First Search
 Hill-climbing: choice of node to
expand is limited to the children of the
node previously expanded.
 Greedy Best-first search: all nodes in
the open set are considered and the
one with the smallest h value is
expanded next.
Difference between hill-climbing
and greedy Best First Search
 Hill-climbing: choice of node to expand is limited to
the children of the node previously expanded.
 Greedy Best-first search: all nodes in the open set
are considered and the one with the smallest h
value is expanded next.
Another way to understand the difference:
 Greedy Best-first search uses a heap as a
priority queue, while hill-climbing uses a
stack.
Priority queue implementation
 Priority queue:
 Insert
 Delete-min
in matlab (ineffciently):
 Insert(A, x):
A(end+1) = x
 Delete-min(A):

[min, i] = min(A); A(i) = [] ;
 Faster version will be provided
when needed.
 Data structures:
 Binary heap
 Binomial heap, pairing heap, …
Greedy best-first search
• Evaluation function f(n) = h(n) (heuristic)
= estimate of cost from n to goal
• e.g., hSLD(n) = straight-line distance from n to
Bucharest
• Greedy best-first search expands the node that
appears to be closest to goal.
Greedy best-first search example
Greedy best-first search example
Greedy best-first search example
Greedy best-first search example
Greedy best first search
h(n) = number of
misplaced tiles
Problems with Greedy Search
• Not complete
•
•
•
•
Get stuck on local minima and plateaus
Irrevocable
Infinite loops
Can we incorporate heuristics in systematic
search?
Modified heuristic for 8-puzzle
best-first search
• Idea: avoid expanding paths that are
already expensive
Evaluation function f(n) = g(n) + h(n)
– g(n) = cost so far to reach n
– h(n) = estimated cost from n to goal
– f(n) = estimated total cost of path through
n to goal
26
Luger: Artificial Intelligence, 6th edition. © Pearson Education Limited, 2009
Admissible heuristics
• A heuristic h(n) is admissible if for every node n,
h(n) ≤ h*(n), where h*(n) is the true cost to
reach the goal state from n.
• An admissible heuristic never overestimates
the cost to reach the goal, i.e., it is optimistic
Example: hSLD(n) (never overestimates the actual
road distance)
When best-first search is implemented
with an admissible heuristic function
h(n), it is called A* algorithm.
The above version is not as efficient as the one
shown in slide 26 so use the former when you
implement A*.
28
A* search: Example 1
A* search example
A* search: Example 1
A* search example
A* search example
A* search example
f(n) = g(n) + h(n) where h(n) is tiles out of place
Optimality of A*
Recall:
 A heuristic h(n) is admissible if for every node n, h(n) ≤
h*(n), where h*(n) is the true cost to reach the goal
state from n.
 An admissible heuristic never overestimates the cost to
reach the goal, i.e., it is optimistic
 Example: hSLD(n) (never overestimates the actual road
distance)
Theorem: A*, when used with admissible h(n), is
optimal.
Maze search with different search
techniques
(c) Uses greedy best-first search
Monotonic h function is also called consistent function.
monotonic heuristic - properties
• If h is monotonic, we have
•
f(n')= g(n') + h(n')
= g(n) + c(n,a,n') + h(n')
≥ g(n) + h(n)
= f(n)
• i.e., f(n) is non-decreasing along any path.
Admissible heuristics
 E.g., for the 8-puzzle:
 h1(n) = number of misplaced tiles
 h2(n) = total Manhattan distance
(i.e., no. of squares from desired location of
each tile)
 h1(S) = ?
 h2(S) = ?
Admissible heuristics
 E.g., for the 8-puzzle:
 h1(n) = number of misplaced tiles
 h2(n) = total Manhattan distance (i.e., no. of squares
from desired location of each tile)
 h1(S) = 8
 h2(S) = 3+1+2+2+2+3+3+2 = 18
Dominance
 If h2(n) ≥ h1(n) for all n (both admissible)
then h2 dominates h1
h2 is better for search
Claim: If h2 dominates h1, then every node
expanded by h2 is also expanded by h1
Effectiveness of A* Search Algorithm
Average number of nodes expanded
d
IDS
A*(h1)
A*(h2)
2
10
6
6
4
112
13
12
8
6384
39
25
12
364404
227
73
14
3473941
539
113
20
------------
7276
676
Study by
Rina Dechter
of UCI.
Average over 100 randomly generated 8-puzzle problems
h1 = number of tiles in the wrong position
h2 = sum of Manhattan distances
Relaxed problems
 A problem with fewer restrictions on the actions is
called a relaxed problem
 The cost of an optimal solution to a relaxed problem is
an admissible heuristic for the original problem
 If the rules of the 8-puzzle are relaxed so that a tile
can move anywhere, then h1(n) gives the shortest
solution
 If the rules are relaxed so that a tile can move to any
adjacent square, then h2(n) gives the shortest solution
Inventing Heuristics automatically
• Examples of Heuristic Functions for A*
How can we invent admissible heuristics in
general?
– look at “relaxed” problem where
constraints are removed
•e.g.., we can move in straight lines
between cities
•e.g.., we can move tiles independently
of each other
Iterative deepening A*
Summary
• In practice we often want the goal with the minimum
cost path.
• Exhaustive search is impractical except on small
problems.
• Heuristic estimates of the path cost from a node to the
goal can be efficient in reducing the search space.
• The A* algorithm combines all of these ideas with
admissible heuristics (which underestimate),
guaranteeing optimality.
• Properties of heuristics:
– admissibility, monotonicity, dominance, accuracy