* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Informed search algorithms
Survey
Document related concepts
Transcript
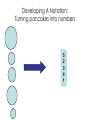
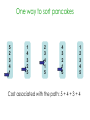
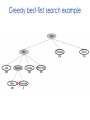
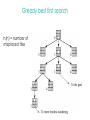
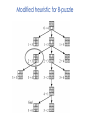
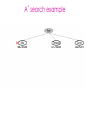
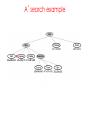
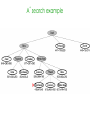
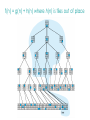
Lecture 3 Jan 28, 2014 • Chapter 3 (BFS, iterative deepening) • Chapter 4 • Informed search Outline • Greedy search – greedy depth-first search – best-first search • A* search • Properties of Heuristics – Admissibility, monotonicity, etc. • Memoized search (a.k.a. dynamic programming) • Automatic generation of heuristics Heuristic - estimate of distance to goal Uninformed search - children (successors) of a node were considered in arbitrary order. Heuristic search – successors are compared to determine which one is more likely to lead to a solution. Search cost – if the edges are weighted, moving from p to q incurs a cost of w(p, q). Sliding piece puzzle (8-puzzle) Cost of each sliding move = 1 Heuristic: number of misplaced tiles Our search heuristic moves as quickly toward the goal as possible. We will select the move of moving the blank to the left in Figure 4.1. Extending this analysis will lead us to move the blank up next and then to the right, arriving at the goal configuration after three moves. Maze search problem Goal: Find a path from s to g. s g Heuristic: distance from node n to g disregarding the barriers. Does not work well in this example. Greedy depth-first search algorithm (hill-climbing) Romania with step costs in km Pancake sorting problem • Several pancakes are on a plate. • Goal is to sort them (so that the largest is at the bottom). • Operation: pick the top k pancakes (using a spatula) and flip them over. • Cost: k units for flipping k pancakes at a time. Developing A Notation: Turning pancakes into numbers 5 2 3 4 1 What is the cost to sort this stack? 5 2 3 4 1 One way to sort pancakes 5 2 3 4 1 1 4 3 2 5 2 3 4 1 5 4 3 2 1 5 1 2 3 4 5 Cost associated with the path: 5 + 4 + 3 + 4 H(n) for some problems • 8-puzzle (sliding piece puzzle) – W(n): number of misplaced tiles – Manhatten distance • Pancake sorting problem – what is a good H? • Unconditional distance to destination in search – Euclidean or Manhattan distance Best-first search • Idea: use an evaluation function f(n) for each node n – estimate of "desirability – Expand most desirable unexpanded node (which need not be a child of the node expanded in the previous step) Difference between hill-climbing and greedy Best First Search Hill-climbing: choice of node to expand is limited to the children of the node previously expanded. Greedy Best-first search: all nodes in the open set are considered and the one with the smallest h value is expanded next. Difference between hill-climbing and greedy Best First Search Hill-climbing: choice of node to expand is limited to the children of the node previously expanded. Greedy Best-first search: all nodes in the open set are considered and the one with the smallest h value is expanded next. Another way to understand the difference: Greedy Best-first search uses a heap as a priority queue, while hill-climbing uses a stack. Priority queue implementation Priority queue: Insert Delete-min in matlab (ineffciently): Insert(A, x): A(end+1) = x Delete-min(A): [min, i] = min(A); A(i) = [] ; Faster version will be provided when needed. Data structures: Binary heap Binomial heap, pairing heap, … Greedy best-first search • Evaluation function f(n) = h(n) (heuristic) = estimate of cost from n to goal • e.g., hSLD(n) = straight-line distance from n to Bucharest • Greedy best-first search expands the node that appears to be closest to goal. Greedy best-first search example Greedy best-first search example Greedy best-first search example Greedy best-first search example Greedy best first search h(n) = number of misplaced tiles Problems with Greedy Search • Not complete • • • • Get stuck on local minima and plateaus Irrevocable Infinite loops Can we incorporate heuristics in systematic search? Modified heuristic for 8-puzzle best-first search • Idea: avoid expanding paths that are already expensive Evaluation function f(n) = g(n) + h(n) – g(n) = cost so far to reach n – h(n) = estimated cost from n to goal – f(n) = estimated total cost of path through n to goal 26 Luger: Artificial Intelligence, 6th edition. © Pearson Education Limited, 2009 Admissible heuristics • A heuristic h(n) is admissible if for every node n, h(n) ≤ h*(n), where h*(n) is the true cost to reach the goal state from n. • An admissible heuristic never overestimates the cost to reach the goal, i.e., it is optimistic Example: hSLD(n) (never overestimates the actual road distance) When best-first search is implemented with an admissible heuristic function h(n), it is called A* algorithm. The above version is not as efficient as the one shown in slide 26 so use the former when you implement A*. 28 A* search: Example 1 A* search example A* search: Example 1 A* search example A* search example A* search example f(n) = g(n) + h(n) where h(n) is tiles out of place Optimality of A* Recall: A heuristic h(n) is admissible if for every node n, h(n) ≤ h*(n), where h*(n) is the true cost to reach the goal state from n. An admissible heuristic never overestimates the cost to reach the goal, i.e., it is optimistic Example: hSLD(n) (never overestimates the actual road distance) Theorem: A*, when used with admissible h(n), is optimal. Maze search with different search techniques (c) Uses greedy best-first search Monotonic h function is also called consistent function. monotonic heuristic - properties • If h is monotonic, we have • f(n')= g(n') + h(n') = g(n) + c(n,a,n') + h(n') ≥ g(n) + h(n) = f(n) • i.e., f(n) is non-decreasing along any path. Admissible heuristics E.g., for the 8-puzzle: h1(n) = number of misplaced tiles h2(n) = total Manhattan distance (i.e., no. of squares from desired location of each tile) h1(S) = ? h2(S) = ? Admissible heuristics E.g., for the 8-puzzle: h1(n) = number of misplaced tiles h2(n) = total Manhattan distance (i.e., no. of squares from desired location of each tile) h1(S) = 8 h2(S) = 3+1+2+2+2+3+3+2 = 18 Dominance If h2(n) ≥ h1(n) for all n (both admissible) then h2 dominates h1 h2 is better for search Claim: If h2 dominates h1, then every node expanded by h2 is also expanded by h1 Effectiveness of A* Search Algorithm Average number of nodes expanded d IDS A*(h1) A*(h2) 2 10 6 6 4 112 13 12 8 6384 39 25 12 364404 227 73 14 3473941 539 113 20 ------------ 7276 676 Study by Rina Dechter of UCI. Average over 100 randomly generated 8-puzzle problems h1 = number of tiles in the wrong position h2 = sum of Manhattan distances Relaxed problems A problem with fewer restrictions on the actions is called a relaxed problem The cost of an optimal solution to a relaxed problem is an admissible heuristic for the original problem If the rules of the 8-puzzle are relaxed so that a tile can move anywhere, then h1(n) gives the shortest solution If the rules are relaxed so that a tile can move to any adjacent square, then h2(n) gives the shortest solution Inventing Heuristics automatically • Examples of Heuristic Functions for A* How can we invent admissible heuristics in general? – look at “relaxed” problem where constraints are removed •e.g.., we can move in straight lines between cities •e.g.., we can move tiles independently of each other Iterative deepening A* Summary • In practice we often want the goal with the minimum cost path. • Exhaustive search is impractical except on small problems. • Heuristic estimates of the path cost from a node to the goal can be efficient in reducing the search space. • The A* algorithm combines all of these ideas with admissible heuristics (which underestimate), guaranteeing optimality. • Properties of heuristics: – admissibility, monotonicity, dominance, accuracy