Download Game Theory application to Networking Research: Part IV.

Applications of Game Theory
Part II(b)
John C.S. Lui
Computer Science & Eng. Dept
The Chinese University of Hong Kong
First course
On the interaction between Overlay
Routing and Underlay Routing
Y. Liu, H. Zhang, W. Gong, D. Towsley
INFOCOM 2005
Motivation: Interactions Between
Application Level Network and Physical
Network
 physical network
control
– routing, congestion
control,…
 add an overlay
 and another……
Result?
– interactions?
– controllers mismatch?
Control
Outline




Problem Formulation
Simulation Study
Game-theoretic Study
Conclusions
Routing in Underlay Network
 Routing on physical network level
 Inter-domain: BGP, etc.
 Intra-domain: OSPF, MPLS, etc.
– determine routes for all source-destination
traffic demand pairs
– minimize network-wide delay, cost, etc.
traffic demand pair: A->B
traffic demand pair: A->C
traffic demand pair: C->B
C
D
E
A
B
Routing in Overlay Network
 An overlay
network choose
routes at
application level
to minimize its
own delay or cost
Overlay demand: A->B
logical routes: A->C->B and A->B
C
A
 Overlay
 gains advantage
potential performance
degradation to other
non-overlay traffic
C
D
better path: delay,
loss, throughput, etc
 is selfish
B
E
A
B
demand pair: A->C
demand pair: C->B
demand pair: A->B
Considering
overlay and underlay
together ?
 How do they interact with each other?
 How does selfish behavior of overlay
routing
– affect overall network performance?
– affect non-overlay traffic
performance?
– affect its own performance?
Interactions Between
Overlay Routing and Underlay Routing
overlay
traffic demand
Overlay Routing Optimizer
To minimize overlay cost
flow allocation on physical routes: “Y”
flow allocation on logical links: “X”
traffic demand for underlay
Underlay Routing Optimizer
To minimize overall network cost
Iterative Dynamic Process
non-overlay
traffic demand
 equilibrium: existence? uniqueness?
 dynamic process: convergence? oscillations?
 performance of overlay and underlay traffic?
Approach by authors
 Focusing interaction in a single AS
 Considering two routing models for overlay
and one routing model for underlay
 Simulating the interaction dynamic process
 Studying this process in a Game-theoretic
framework
Routing Models
 Overlay routing model
– Selfish source routing
 Individual user controls infinitesimal amount of
traffic, to minimize its own delay
– Optimal overlay routing
 A central entity minimizes the total delay of all
overlay traffic demands
 Underlay routing model
 Optimal underlay routing
 A central entity minimizes the total delay of all network
traffic, e.g. Traffic Engineering MPLS
Simulation Study:
Optimal Overlay and Optimal Underlay
14 node tier-1 POP network (Medina et.al. 2002)
bimodal normal model of traffic demand
3 overlay nodes
Node without overlay
Node with overlay
Link
4
7
11
14
3
9
6
12
10
13
1
2
5
8
Simulation Study ( case 1: 8% overlay traffic)
Optimal Overlay and Optimal Underlay
Iterative process
 Underlay takes turn at step 1, 3, 5, …
 Overlay takes turn at step 2, 4, 6, …
average delay of all traffic
iteration
percentage %
percentage %
average delay of overlay traffic
overlay performance
improvement
Delay( k ) - Delay( 1)
100%
Delay( 1)
k  1,2,3,4,5,...
underlay performance
degradation
after underlay takes turn
after overlay takes turn
iteration
Simulation Study (case 2: 10% overlay traffic)
Optimal Overlay and Optimal Underlay
Iterative process
 Underlay takes turn at step 1, 3, 5, …
 Overlay takes turn at step 2, 4, 6, …
overlay performance
degradation
average delay of all traffic
percentage %
percentage %
average delay of overlay traffic
Delay( k ) - Delay( 1)
100%
Delay( 1)
k  1,2,3,4,5,...
underlay performance
degradation
iteration
iteration
after underlay takes turn
after overlay takes turn
Game-theoretic Study
 Two-player non-zero sum game
Underlay
overlay
X: strategy of “overlay” traffic allocation on logical links
Y: strategy of “underlay” traffic allocation on physical links
: Cost of “overlay”
: Cost of “underlay”
: Constraints of “overlay”
: Constraints of “underlay”
Game-theoretic Study
• Best-reply dynamics
• Nash Equilibrium
Optimal Underlay Routing v.s.
Optimal Overlay Routing
 Overlay
– One central entity calculates routes for all
overlay demands, given current underlay routing
– Assumption: it knows underlay topology and
background traffic
C
X(k)
A
1-X(k)
B
Denote overlay’s routing decision with a single variable X(k):
overlay’s flow on path ACB after round k
Best-reply Dynamics
 There exists unique Nash equilibrium x*,
 x* globally stable: x(k) x*, from any initial x(1)
When x(1)=0, overlay performance improves
x(k)
x*
Overlay Delay Evolution
delay
Overlay Routing Evolution
Underlay’s turn
Overlay’s turn
x(k)<x(k+1)<x*
iteration k
iteration k
Best-reply Dynamics
 There exists unique Nash equilibrium x*,
 x* globally stable: x(k) x*, from any initial x(1)
When x(1)=0.5, overlay performance degrades
x(k)
x*
x(k)>x(k+1)>x*
Overlay Delay Evolution
delay
Overlay Routing Evolution
Underlay’s turn
Overlay’s turn
x(k)<x(k+1)<x*
Round k
Round k
Conclusions & Open Issues
 Selfish overlay routing can degrade
performance of network as a whole
 Interactions between blind optimizations at
two levels may lead to lose-lose situation
 Future work:
–
–
–
–
–
larger topology: analysis/experimentation
overlay routing and inter-domain routing
interactions between multiple overlays (****)
implications on design overlay routing
regulation between overlay and underlay (****)
Second course
On the Interaction of Multiple Overlay
Routings
Performance 2005
Joe W.J. Jiang, D.M. Chiu, John C.S. Lui
Questions
• These overlays tend to fully utilize available
resource.
• So, is there any anarchy?
• How do overlay networks co-exist with each
other?
• What is the implication of interactions?
• How to regulate selfish overlay networks via
mechanism design?
• Can ISPs take advantage of this?
Outline
•
•
•
•
•
•
Motivation
Mathematical Modeling
Overlay Routing Game
Implications of Interaction
Pricing
Conclusion
Motivation
• Overlays provide a feasibility for users to
control their own routing.
• Routing, possible multi-path, becomes an
optimization problem.
• Interaction occurs (due to same underlay)
• Interaction between one overlay and underlay
Adaptive routing controls
Simultaneous feedback
traffic
engineering,
Zhangcontrols
et al,over
Infocom’05.
on multiple
layers
one system
(overlays, underlay
TE --co-existing overlays ?
• Interaction
between
Stability ?
traffic engineering) over
one common physical
network
Performance ?
Performance Characteristics
• Objective: minimize end-to-end delay (e.g., RON)
• Delay of a physical link e:
de(le)
•
l
– aggregate traffic traversing link e
e
Performance Characteristics (Underlay)
Average delay ( f : flow)
 f  d  f 
f  s ,t
Performance Characteristics
• Objective: minimize end-to-end delay
• Delay of a physical link e:
de(le)
le – aggregate
traffic traversing
link e
• Performance
Characteristics
(Underlay)
Average delay (multipath routing)
   f
f  s ,t rP f
r
 d  fr 
Performance Characteristics
• Objective: minimize end-to-end delay
• Delay of a physical link e:
de(le)
le – aggregate traffic traversing link e
• Performance Characteristics (Underlay)
Average delay (multipath routing)
l
e
e
 d e le 
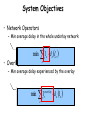
System Objectives
• Network Operators
– Min average delay in the whole underlay network
min
• Overlay Users
l
e
 d e le 
e
– Min average delay experienced by the overlay
min
overlay
l
 e  de le 
e
How do Overlays Interact?
•
•
•
•
•
Overlapping physical links.
Performance dependent on each other.
Selfish routing optimization.
Overlays are transparent to each other.
Lack of information exchange between
overlays.
Contribution
• What is the form of interaction?
• Is there routing instability (oscillation), or
there is an equilibrium ?
• Is the routing equilibrium efficient?
• What is the price of anarchy?
• Fairness issues
• Mechanism design: can we lead the selfish
behaviors to an efficient equilibrium?
Mathematical Modeling
• Overlay routing: An optimization problem

Decision variable: routing policy
s: overlay
y
(s)
f: flow

 y

( s ,1)
,y
( s , 2)
r: path
,, y

( s, f ) T
y ( s , f )  y1( s , f ) , y2( s , f ) ,, yr( s , f )

Mathematical Modeling
• Overlay routing: An optimization problem
Objective: average weighted delay
(matrix form)

delay ( s )  
f
delay
(s)
y
s, f 
y
 r  delay r
rR  f
( s )T
Routing Matrix

 ( s )T 
( i ) ( i ) 
 A D  A y 
 i


Delay Function
(vector form)
Overlay Routing Optimization

Convex programming
OVERLAY ( s )
Minimize
s.t.
y
(s)
; A, H , C , x, y (  s )

 ( s )T 
( i ) ( i ) 
delay  y  A D  A y 
 i


f  Fs ,  yr( s , f )  x f
( s )T
(s)
rR f

Capacity Constraint
Ay  C , y ( s )  0


Non-negative Flow Constraint
Demand constraint
(fixed transmission demand)
Algorithmic Solution
• Unique optimizer
– Convex programming
– feasible region: convex
– delay function: continuous, non-decreasing, strictly
convex
• Solution
– Apply any convex programming techniques.
– Marginal cost network flow (probabilistic routing
ICNP’04).
– This is solved in an independent, and distributed
fashion by each overlay.
But will independent optimization leads to system instability (route flop)?
Overlay Routing Game
Strategic Game: Goverlay<N, (s), (≥s)>
• Nash Routing Game
– Player -- N
all overlays
– Strategy -- s
feasible routing policy: feasible region of OVERLAY(s)
– Preference relation -- ≥s
low delay: player’s utility function is -delay(s)
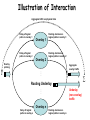
Illustration of Interaction
Aggregate traffic on physical links
Delay of logical
paths in overlay 1
Overlay 1
Delay of logical
paths in overlay 2
Routing decision on
logical paths in overlay 1
Routing decision on
logical paths in overlay 2
Overlay 2
Overlay
probing
Aggregate
overlay traffic
…
∑
Routing Underlay
…
Underlay
(non-overlay)
traffic
Delay of logical
paths in overlay n
Overlay n
Routing decision on
logical paths in overlay n
Existence of Nash Equilibrium
• Definition – Nash equilibrium point (NE)
A feasible strategy profile
y=(y(1),…, y(s),…, y(n))T
is a Nash equilibrium in the overlay routing
game if for every overlay s∈N,
≤
delay(s)(y(1),…y(s),…y(n))
delay(s)(y(1),…y’(s),…y(n))
for any other feasible strategy profile y’(s) .
Existence of Nash Equilibrium
• Theorem Good News: NO ROUTE FLOP !!!
In the overlay routing game, there exists a
Nash equilibrium if the delay function
delay(s)(y(s) ; y(-s))
is continuous, non-decreasing and convex.
Fluid Simulation

Six overlays
One flow per
overlay

Congested
network

Asynchronous
routing update

Overlay performance
Transient period
Quick
convergence
Overlay routing decisions
The Price of Anarchy
Global Performance (average delay for all flows)
0
1
GOR
2
3
4
5
6
NOR
7
8
...
NSR
Efficiency Loss ?
• GOR: Global Optimal Routing
• NOR: Nash equilibrium for Overlay Routing Game
• NSR: Nash equilibrium for Selfish Routing
...

Selfish Routing
• (User) selfish routing: a single packet’s selfishness
• Every single packet chooses to route via a shortest
(delay) path.
• A flow is at Nash equilibrium if no packet can improve its
delay by changing its route.
 fP  
~ 
P1  P2 ,   [0, f P1 ], if f P   f P  
f
 P
~
d P1 ( f )  d P2 ( f )
if P  P1
if P  P2
otherwise
Selfish Routing
• Also a Nash equilibrium of a mixed strategic
game
– Player: flow { f }
– Strategy: p  Pf
– Preference: low delay
• System Optimization Problem
SELFISH
min
 y; A, H , C , x 
l
 0 d e t dt
e
e
s.t.
Hy  x, Ay  C , L  Ay, y  0
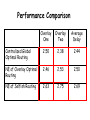
Performance Comparison
Overlay
One
Overlay
Two
Average
Delay
Centralized Global
Optimal Routing
2.50
2.38
2.44
NE of Overlay Optimal
Routing
2.46
2.53
2.50
NE of Selfish Routing
2.63
2.75
2.69
Inspiration
• Is the equilibrium point efficient (at least
Pareto optimal) ?
• Fairness issues of resource competition
between overlays.
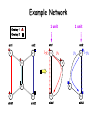
Example Network
1 unit
1 unit
Overlay 1
Overlay 2
src1
src2
1
2
src2
src1
1-y1
1
3
y1
y2
2
3
4
4
5
6
5
6
sink1
sink2
sink1
sink2
1-y2
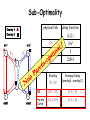
Sub-Optimality
Overlay 1
Overlay 2
src1
1
physical link
delay function
1-5
3-4
de(le)
1+l
l
2-6
2.5+l
src2
y1
y2
2
3
Routing
(y1, y2)
Average Delay
(overlay1, overlay2 )
NE
(0.5, 1.0)
(1.5, 1.5)
Pareto
Curve
(0.4, 0.9)
(1.4, 1.4)
4
5
6
sink1
sink2
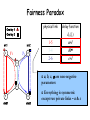
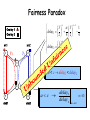
Fairness Paradox
Overlay 1
Overlay 2
src1
1
src2
y1
y2
2
physical link
delay function
1-5
3-4
2-6
de(le)
a+l
bl
c+l
3
a, b, c,  are non-negative
parameters

4
5
6
sink1
sink2
Everything is symmetric
except two private links – a & c

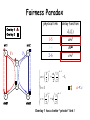
Fairness Paradox
Overlay 1
Overlay 2
src1
1
src2
y1
y2
2
physical link
delay function
1-5
3-4
2-6
de(le)
a+l
bl
c+l
3
4
5
6
sink1
sink2

 1

3  3
a

      1,

2 2
2


b  1


 1
3
3
c       
  2 
2
Overlay 1 has a better “private” link !
a<c
Fairness Paradox
Overlay 1
Overlay 2
src1
1
src2
y1
y2
2

 1

3

3
1
 
 
delay1       
4 2
4

2


3

delay

 
2

2

3
a < c  delay1 < delay2
4
5
6
sink1
sink2
ac 
delay1
delay 2

 
War of Resource Competition
1 unit
USA
1 unit
y2
y1
poil(y1+y2)
China
Min Costusa(y1 ; y2) =
1-y1
y1poil(y1+y2)+(1-y1)pusa(1-y1)
pusa(1-y1)
pusa< pchn
pchn(1-y2)
1-y2
War of Resource Competition
1 unit
USA
1 unit
y2
y1
poil(y1+y2)
China
Min Costchn(y2 ; y1) =
1-y1
y2poil(y1+y2)+(1-y2)pchn(1-y2)
pusa(1-y1)
pusa< pchn
pchn(1-y2)
1-y2
War of Resource Competition
1 unit
1 unit
USA
China
poil(y1+y2)
pusa< pchn
 Costusa > Costchn
pusa(1-y1)
pchn(1-y2)
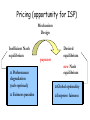
Pricing (opportunity for ISP)
Mechanism
Design
Inefficient Nash
equilibrium
Performance
degradation
(sub-optimal)
Desired
equilibrium
payment
new Nash
equilibrium


Fairness paradox

Global optimality

Improve fairness
Pricing I – Improve Delay
• Objective: to achieve global optimality
• NE of overlay
routing game
min

(s)
(s)
(s)
l

d
l

l
e e e e
e
le(s) : traffic of overlay s
le(-s) : traffic other than
overlay s
• Global optimal

min
l
e
 d e le 
e
le  le( s )  le(  s )
Pricing I – Improve Delay
• Objective: to achieve global optimality
• New NE of overlay
routing game
• Global optimal
min delay ( s )  payment ( s )
min
l
e
 d e le 
e
min
 l
(s)
e

 d e le( s )  le(  s )

e
  le( s )  pe( s )
e
Heterogeneous pricing
le  le( s )  le(  s )
Pricing I – Improve Delay
• Global optimal
• New NE of overlay
routing game
min
 

(s)
(s)
(s)
(s)
l

d
l

l

p
e e e e
e

KKT condition:
 l  d l
er
(s)
e
  d e le   p
er
 ur
l
e
 d e le 
e
e
(s)
e
min
KKT condition:
l
(s)
e
(s)
e
l
(s)
e
  p 
(s)
e
'
 d le 
'
e
pe(s)=le(-s)
'




l

d
l
 e e e
er
  d e le   le  d e' le 
er
 ur
’
de (le)
Pricing II – improve fairness
• Cause of unfairness:
– Over-utilize good common resources
– Unfair resource (bandwidth) allocation
• Pricing Scheme
price p
ISP
Overlay
maximize profit
Improve performance
& Reduce cost
routing decision
Incentive Resource Allocation
• For overlays:
min Cost ( s ) y ( s ) ; y (  s )    s  delay ( s )  payment ( s )
  s   le( s )  d e le    pe  le( s )
e
 s : sensitivity factor
new Nash equilibrium  {le}
e
Revenue Distribution
• For ISPs (links):
max Ple   pe  le  ce le 
Pe le  : profit of link e
pe  le : revenue
ce le  : operating cost -- log le  d e le 
'
d
dP
1
'
e le 
 0  pe  ce le   
dle
le d e le 
Effectiveness of Pricing
Conclusion
• Study the interaction between multiple coexisting overlays.
• Non-cooperative Nash routing game.
• Prove the existence of NEP.
• Show the anomalies and implications of the NEP.
• Present two distributed pricing schemes to
address the anomalies.
Third Course
Interaction of ISPs: Distributed
Resource Allocation and Revenue
Maximization
Sam C.M. Lee, Joe W.J. Jiang,
D.M Chiu, John C.S. Lui
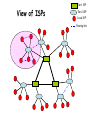
View of ISPs
Tier-1 ISP
Tier-2 ISP
Local ISP
Peering link
Tier-2 ISP
Local ISP
ISP
Peer
Peer
Peer
Peering link
ISP link
ISP
Peer
Peer
Peer
Optimization problem of peers
Issues to consider:
Peer i
Tier-2 ISP
(ISP)
Peer j
1. performance of the link
2. charge of the link
Peer k
Optimization problem of peers
Happiness obtained from
sending traffic to peers
Delay cost in ISP link
Payment to ISP
Delay costs in peering links
Payments to peers
Constraints of peers
1.
2.
3.
4.
Solution to the peers
• Objective function is strictly concave in
every transmission rate
• The optimal transmission rates and
maximum utility are unique and can be
found by the Lagrangian method.
Problems for an ISP
• Resource distribution
– How to determine the capacity for the
peers
• Maximization of revenue
– How to determine the optimal value of unit
price
Information exchange framework
Next period
Bandwidth
allocation
Bid
ISP
peer
Compute
resource
distribution
Compute
optimal
rates
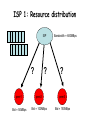
ISP 1: Resource distribution
ISP
?
?
Bandwidth = 600MBps
?
peer1
peer2
peer3
Bid = 50MBps
Bid = 100MBps
Bid = 150MBps
Proportional share algorithm
ISP
100MBps
Bandwidth = 600MBps
200MBps
300MBps
peer1
peer2
peer3
Bid = 50MBps
Bid = 100MBps
Bid = 150MBps
Equal share algorithm
ISP
150MBps
Bandwidth = 600MBps
200MBps
250MBps
peer1
peer2
peer3
Bid = 50MBps
Bid = 100MBps
Bid = 150MBps
Simulations
• When the happiness coefficients of peers are low
PSA
ESA
Simulation
• When the happiness coefficients of peers are high
PSA
ESA
ISP 2: Maximization of Revenue
Unit price
Demand by peer i
Total revenue from the peers
Determine the optimal price
Solution: Maximization of revenue
•Estimate the aggregate traffic (
peers in term of the price (P)
) from all
Conclusions
• Utility maximization of a peer
• Resource distribution of ISP
• Revenue maximization of ISP
Fourth Course
On the Access Pricing Issues of
Wireless Mesh Networks
ICDCS 2006
Ray K. Lam
Dah-Ming Chiu
John C.S. Lui
WMN Paints a Bright Future
• Wireless mesh network
(WMN)
– Wireless nodes
– Multi-hop routing
– Form a wireless “mesh”
• More access to the
Internet
– More people, rich or poor
– More ubiquitous, anywhere,
anytime
– More opportunities to
everyone
Internet
Internet
The Critical Thing—Cooperation
Multi-hop routing
Relay
packets for each other
My concerns: bandwidth, CPU time, security…
Community network with symmetric traffic
Help
each other => mutual benefit
Access network with asymmetric traffic
Geographically
good VS poor
Why help the poor?
Incentive system needed—pricing
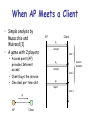
When AP Meets a Client
• Simple analysis by
Musacchio and
Walrand [1]
• A game with 2 players
– Access point (AP)
provides Internet
access
– Client buys the service
– One deal per time slot
AP
Client
p1
accept
slot 1
p2
service
duration
accept
slot 2
p3
reject
slot 3
p
AP
Client
A Beautiful Equilibrium
• AP and client each maximizes
her gain
– AP: guess the “right” price
– Client: compare the price p with
service utility U
• Web browsing utility function
• A beautiful equilibrium
– AP has the same optimal price in every time slot
– Client connects if her per-slot service utility is
greater than slot price (U > p)
• Encourages flat-rate pricing
To a Multi-hop Scenario
• Adding a relaying node, or
“reseller” (RS)
p
• RS tries
to mark up AP’s
c
price to the “right” level
AP
RS
Client
• AP takes note of RS’s
action when setting her
price
• Equilibrium is still flatrate pricing
• Multi-hop => multiple RSs
AP
RS
Client
c1
p1
accept
accept
c2
p2
accept
accept
c3
p3
reject
reject
slot 1
service
duration
slot 2
slot 3
Drawbacks of the Simple Model
• Assuming unlimited network capacity
– 2-player game represents whole
system
– Treat every incoming client the
same
– Unlimited admission => unlimited
capacity
• Assuming a tree-like network
– 2-hop / multi-hop linear network
extension
– Does not consider multiple paths
– Pricing competition may occur
AP
RS
Client
A tree-like network
A graph-like network
What If Capacity Limited?
• Cannot admit unlimited clients
– Client demands bandwidth guarantee
– AP admission control
– AP’s system capacity: m
• 2-player game not enough
– AP deals with each client differently
– Client arrival model: Poisson process
• Like an M/M/m/m/M queuing system
Flat-rate Pricing Fails…
• Failure scenario
–
–
–
–
–
AP is full; m clients admitted
An admitted client a is paying $5/slot
A new client b arrives
AP asks b for $6/slot
If b accepts
• AP raises price for a to $6/slot, OR
• Simply kicks a out
• Flat-rate pricing is not optimal!
Everybody Loves Flat Rate
• Unrealistic for variable rate
• More practical—fixed-rate, noninterrupted service
– AP charges a client a fixed rate p over time
– AP cannot disconnect a client unilaterally
• AP can still charge different clients at
different “fixed” rates
– How to set the optimal rate on different
occasions?
Best Strategy in New Service
Model
• AP sets price based on remaining capacity
– Raises price when becoming full
– State price: at state k, AP charges next “to-beadmitted” client at fixed rate pk
– Policy of AP characterized by price vector
• Client’s best strategy
– Connect AP if service utility per unit time > price
per unit time (U > p)
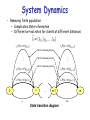
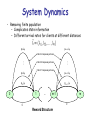
System Dynamics
• State transition
– Adding a factor P(U > pk) to regular
arrival rate in M/M/m/m/M model
• Reward structure
– Simplification: immediate expected
profit when a client connects
 M P(U > p0)
0
 M-1) P(U > p1)
1

 M-m+1) P(U > pm-1)
2
…
2
State transition diagram
m-1
m
m
System Dynamics
• State transition
– Adding a factor P(U > pk) to regular
arrival rate in M/M/m/m/M model
• Reward structure
– Simplification: immediate expected
profit when a client connects
p0/
0
p1/
1
0
pm-1/
2
…
0
Reward Structure
m-1
m
0
Finding Optimal Price Vector
• Classical optimization
– Solution for queuing system gives limiting state
probability for each state k, k
– Gain of AP is a function of price vector
– Complicated to optimize with classical techniques
• Policy-iteration method in Markovian decision
theory
– Reduces computational complexity by iterative algorithm
– Guarantees convergence to the best policy
Numerical Results
• Capacity m=5,
population M=10,
departure rate =1
• Vary arrival rate 
from 0.2 to 10
• Utility U uniformly
distributed on [0,10]
• U normally distributed
with mean 5, s.d. 1.67
• Price increases number
of clients in AP and
with 
Limited Capacity in Multi-hop Case
• Simplification
– Traffic merges at AP
– AP is the bottleneck
– Only AP controls
admission
Internet
bandwidth
bottleneck
AP
RS Client
• AP’s policy specified by a price matrix
– At each state, different prices for requests
from different distances
– pki: price at state k for a client i-hop away
System Dynamics
• Removing finite population
– Complicates state information
– Different arrival rates for clients at different distances
n P(U > mn(p0,n))
n P(U > mn(pm-1,n))
Client n-hop away arrives
Client 1-hop away arrives
…
…
2 P(U >
Client 2-hop away arrives
m2(p0,2))
2 P(U > m2(pm-1,2))
1 P(U > m1(p0,1))
1 P(U > m1(pm-1,1))
0
1
…
m-1

m
m
State transition diagram
System Dynamics
• Removing finite population
– Complicates state information
– Different arrival rates for clients at different distances
p0,n/
pm-1,n/
Client n-hop away arrives
…
…
Client 2-hop away arrives
Client 1-hop away arrives
p0,2/
pm-1,2/
p0,1/
pm-1,1/
0
1
…
m-1
m
0
0
Reward Structure
Conclusion
•
Contributions
–
–
–
•
Show that fixed-rate pricing fails with limited capacity
Generalize unlimited capacity model into limited
capacity model
Devise optimal pricing for fixed-rate, non-interrupted
service with Markovian decision theory
References
[1] J. Musacchio and J. Walrand. WiFi access point pricing
as a dynamic game. IEEE/ACM Trans. Networking. to
appear in.