Download λP.[λQ. ∀x((P@x)→(Q@x))]@ λy.boxer(y)

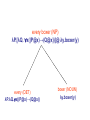
Semantic Construction
lecture 2
Semantic Construction
• Is there a systematic way of constructing
semantic representation from a sentence of
English?
• This question is too ambitious for now.
• Let's begin with a more specific one.
• Is there a systematic way of translating simple
sentences such as:
Vincent likes Mia
Every woman snorts
Every boxer loves a woman
• into 1st-order logic?
Meaning flows from the lexicon
• Assume the natural language sentence Vincent
likes Mia should be represented by the 1st-order
sentence like(vincent,mia).
• The proper name Vincent is what gives rise to
the constant vincent, and Mia is what gives rise
to the constant mia, and the verb likes
contributes the 2-place relation symbol like.
• A simple observation, but it leads to an important
generalization: meaning ultimately flows from
the lexicon.
What about function words?
• Every woman snorts is represented as
Ax(woman(x) → snort(x)).
• What exactly does the word Every
contribute to this representation?
• How can we be precise about what its
contribution is?
Syntax also plays a role
• Why did we get like(vincent,mia) as the
representation and not (say) like(mia,vincent)
– Subject is Vincent
– Object is Mia
• Notions like Subject and Object come from the
syntactic structure of the sentence.
• The basic principle here is that the syntactic
structure of the natural language sentence
should guide the process of semantic
construction.
The three tasks
•
•
•
This gives us a guide to how to proceed. We
need to...
Task 1 Specify a reasonable syntax for the
fragment of natural language of interest.
Task 2 Specify semantic representations for the
lexical items.
Task 3 Specify the translation compositionally.
That is, we should specify the translation of all
expressions in terms of the translation of their
parts.
Task 1:
Specify syntax for NL fragment.
•
•
•
•
•
•
•
Categorial Grammar
Context Free Grammars
Interaction Grammars
Head Driven Phrase Structure Grammar (HPSG)
Lexical Functional Grammar (LFG)
Tree Adjoining Grammars (TAG)
Minimalism, GB, TG, or some other Chomskyan
framework.
• Nice computational choice for a first exploration:
Definite Clause Grammars (DCGs)
Definite Clause Grammar
%grammar
s --> np, vp.
np --> pn.
np --> det, noun.
vp --> iv.
vp --> tv, np.
%lexicon
noun --> [woman]
noun --> [foot,massage].
iv --> [walks].
tv --> [loves].
tv --> [likes].
pn --> [mia].
pn --> [vincent].
det --> [a].
det --> [every].
Definite Clause Grammars
• They are a natural notation for specifying
grammars which automatically have a
computational interpretation.
• For example, by posing the query
?- s([mia,likes,a,foot,massage],[ ])
we can test whether this sentence belongs to the
fragment the grammar describes.
• For more on DCGs, look at Learn Prolog Now!
which is available at
http://www.learnprolognow.org.
• Tasks 2 and 3
The Lambda Calculus
• The lambda operator marks missing information
by binding variables.
• Here is a simple lambda expression λx.man(x)
• The prefix λx binds the occurrence of x in
man(x);
• λx.man(x) can be read as: ‘I am the 1-place
predicate man, and I am looking for a term to fill
my argument slot.
Functional Application
• Functional application The @ operator is used to
indicate “functional application”.
• That is, it indicates that we wish to perform a
substitution. Example:
λx.man(x)@vincent
• The expression λx.man(x) is called the functor.
• The expression vincent is called the argument.
• Bracketing: ( ( λx.man(x) ) @ ( vincent ) )
• Schematically: (functor @ argument)
β -conversion
• The required substitution is performed by
β -conversion (which is sometimes called
β -reduction):
• From λx.man(x)@vincent
• β -conversion produces man(vincent)
• Basically, we throw away the λx. at the
start of the expression, and substitute the
argument for all occurrences of x that were
bound by λx.
When can we β-convert?
• For β-conversion to be applicable, the functor
must have the form λx.expression
• Such expressions are usually called lambda
abstractions, or abstractions.
• That is, given an expression of the form
λx.expression @ argument we can β -convert,
because the functor expression is a lambda
abstraction.
• One the other hand, given an expression of the
form functor @ argument where functor is not of
the form λx.expression, then we cannot β-convert.
More Complex Example
• Our semantic representation of a woman
will be: λQ. ∃x(woman(x) ∧ Q@x)
• We use the variable Q to indicate that:
– some information is missing
– where this information has to be plugged in
– We can use lambda notation to build up
patterns of meaning or patterns of
representation, explicitly indicating where the
various bit and pieces have to be glued into
place.
Every boxer growls
• Step 1: assign lambda expressions to
lexical items
• boxer: λy.boxer(y)
growls: λx.growl(x)
every: λP.λQ. ∀x(P@x→Q@x)
Every Boxer Growls
• Step 2: associate the NP node with the
application that has the DET
representation as functor and the NOUN
representation as argument.
every boxer (NP)
λP.[λQ. ∀x((P@x)→(Q@x))]@ λy.boxer(y)
every (DET)
λP.λQ.∀x((P@x)→(Q@x))
boxer (NOUN)
λy.boxer(y)
Beta Conversion
• The node for Every boxer is an application, and
the left hand expression is an abstraction, so we
can β-convert.
• every boxer:
λP.[λQ. ∀x((P@x)→(Q@x))]@ λy.boxer(y)
• every boxer: λQ. ∀x((λy.boxer(y)@x)→(Q@x))
• But the resulting expression contains a
subexpression λy.boxer(y)@x. So we can β convert again.
• every boxer: λQ. ∀x((λy.boxer(y)@x)→(Q@x))
every boxer: λQ. ∀x(boxer(x)→(Q@x)
•
•
•
•
every boxer: λQ. ∀x(boxer(x)→(Q@x)
growls λy. growl(y)
every boxer(growls)
beta-reduction:
Proper Nouns
• Quantifying noun phrases can clearly be used
as functors.
• But what about NPs like Vincent? If the semantic
representation of Vincent is just the constant
vincent, then we cannot do this.
• Here is a bad answer: say that in such cases we
apply the verb semantics to the noun phrase
semantics.
• Note that this seems to work: applying
λx.growl(x) to vincent yields growl(vincent),
which seems right. So why is it bad?
Handling Proper Names
• Fortunately, there is a very easy way to give a
representation to Vincenta nd other names
which allows us to use the representation as a
functor, and, at the same time, puts the constant
vincent in the right place.
• Vincent: λP.(P@vincent)
• Mia: λP.(P@mia)
• These representations can be used as functors.
In effect they say: apply my argument to the
constant I contain!
Vincent growls
• We can build up the semantic representation for
Vincent growls simple by applying the NP
semantics to the VP semantics.
• NP semantics: λP.(P@vincent)
VP semantics: λw.growls(w)
• λP.(P@vincent) @ λw.growls(w)
(λw.growls(w)@vincent)
growls(vincent )
• Thus the method works.
• In effect we are seeing that NPs are generalised
quantifiers.
Is beta-conversion safe
The representations
• λx.λy.bloogle(x,y)
• λz.λw.bloogle(z,w)
are intended to have the same effect.
• There are situations, however, when they
do not
Is beta conversion safe
• Things can go wrong if we apply a lambda
expression to a variable that occurs bound in the
functor.
• For example, if we apply λx.λy.bloogle(x,y) to the
variable w we obtain λy.bloogle(w,y) which is
what we want.
• On the other hand, if we apply
λz.λw.bloogle(z,w) to w we obtain
λw.bloogle(w,w).
• This is not what we want. The variable w has
become accidentally bound.
α-conversion
• α-conversion is the process of replacing
(renaming) bound variables. e.g. we obtain
λx.λy.bloogle(x,y) from λz.λw.bloogle(z,w) by αconversion
• To prevent accidental binding, we always αconvert before carrying out β -conversion.
• In particular, we always rename all the bound
variables in the functor so they are distinct from
all the variables in the argument.
• So our fundamental combination method is
really α-conversion (for safety) followed by β conversion.