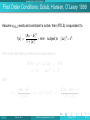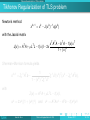* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Large–Scale Tikhonov Regularization for Total Least
Perturbation theory wikipedia , lookup
Lateral computing wikipedia , lookup
Genetic algorithm wikipedia , lookup
Computational fluid dynamics wikipedia , lookup
Numerical continuation wikipedia , lookup
Computational complexity theory wikipedia , lookup
Simplex algorithm wikipedia , lookup
Newton's method wikipedia , lookup
Linear least squares (mathematics) wikipedia , lookup
Renormalization wikipedia , lookup
Mathematical optimization wikipedia , lookup
Multiple-criteria decision analysis wikipedia , lookup
Inverse problem wikipedia , lookup
False position method wikipedia , lookup
Large–Scale Tikhonov Regularization for Total Least Squares Problems Heinrich Voss [email protected] Joint work with Jörg Lampe Hamburg University of Technology Institute of Numerical Simulation TUHH Heinrich Voss Tikhonov Regularization for TLS Bremen 2011 1 / 24 Outline 1 Total Least Squares Problems 2 Regularization of TLS Problems 3 Tikhonov Regularization of TLS problems 4 Numerical Experiments 5 Conclusions TUHH Heinrich Voss Tikhonov Regularization for TLS Bremen 2011 2 / 24 Total Least Squares Problems Outline 1 Total Least Squares Problems 2 Regularization of TLS Problems 3 Tikhonov Regularization of TLS problems 4 Numerical Experiments 5 Conclusions TUHH Heinrich Voss Tikhonov Regularization for TLS Bremen 2011 3 / 24 Total Least Squares Problems Total Least Squares Problems The ordinary Least Squares (LS) method assumes that the system matrix A of a linear model is error free, and all errors are confined to the right hand side b. However, in engineering applications this assumption is often unrealistic. Many problems in data estimation are obtained by linear systems where both, the matrix A and the right-hand side b, are contaminated by noise, for example if A as well is only available by measurements or if A is an idealized approximation of the true operator. If the true values of the observed variables satisfy linear relations, and if the errors in the observations are independent random variables with zero mean and equal variance, then the total least squares (TLS) approach often gives better estimates than LS. Given A ∈ Rm×n , b ∈ Rm , m ≥ n Find ∆A ∈ Rm×n , ∆b ∈ Rm and x ∈ Rn such that k[∆A, ∆b]k2F = min! subject to (A + ∆A)x = b + ∆b, (1) where k · kF denotes the Frobenius norm. TUHH Heinrich Voss Tikhonov Regularization for TLS Bremen 2011 4 / 24 Total Least Squares Problems Total Least Squares Problems The ordinary Least Squares (LS) method assumes that the system matrix A of a linear model is error free, and all errors are confined to the right hand side b. However, in engineering applications this assumption is often unrealistic. Many problems in data estimation are obtained by linear systems where both, the matrix A and the right-hand side b, are contaminated by noise, for example if A as well is only available by measurements or if A is an idealized approximation of the true operator. If the true values of the observed variables satisfy linear relations, and if the errors in the observations are independent random variables with zero mean and equal variance, then the total least squares (TLS) approach often gives better estimates than LS. Given A ∈ Rm×n , b ∈ Rm , m ≥ n Find ∆A ∈ Rm×n , ∆b ∈ Rm and x ∈ Rn such that k[∆A, ∆b]k2F = min! subject to (A + ∆A)x = b + ∆b, (1) where k · kF denotes the Frobenius norm. TUHH Heinrich Voss Tikhonov Regularization for TLS Bremen 2011 4 / 24 Total Least Squares Problems Total Least Squares Problems The ordinary Least Squares (LS) method assumes that the system matrix A of a linear model is error free, and all errors are confined to the right hand side b. However, in engineering applications this assumption is often unrealistic. Many problems in data estimation are obtained by linear systems where both, the matrix A and the right-hand side b, are contaminated by noise, for example if A as well is only available by measurements or if A is an idealized approximation of the true operator. If the true values of the observed variables satisfy linear relations, and if the errors in the observations are independent random variables with zero mean and equal variance, then the total least squares (TLS) approach often gives better estimates than LS. Given A ∈ Rm×n , b ∈ Rm , m ≥ n Find ∆A ∈ Rm×n , ∆b ∈ Rm and x ∈ Rn such that k[∆A, ∆b]k2F = min! subject to (A + ∆A)x = b + ∆b, (1) where k · kF denotes the Frobenius norm. TUHH Heinrich Voss Tikhonov Regularization for TLS Bremen 2011 4 / 24 Total Least Squares Problems Total Least Squares Problems The ordinary Least Squares (LS) method assumes that the system matrix A of a linear model is error free, and all errors are confined to the right hand side b. However, in engineering applications this assumption is often unrealistic. Many problems in data estimation are obtained by linear systems where both, the matrix A and the right-hand side b, are contaminated by noise, for example if A as well is only available by measurements or if A is an idealized approximation of the true operator. If the true values of the observed variables satisfy linear relations, and if the errors in the observations are independent random variables with zero mean and equal variance, then the total least squares (TLS) approach often gives better estimates than LS. Given A ∈ Rm×n , b ∈ Rm , m ≥ n Find ∆A ∈ Rm×n , ∆b ∈ Rm and x ∈ Rn such that k[∆A, ∆b]k2F = min! subject to (A + ∆A)x = b + ∆b, (1) where k · kF denotes the Frobenius norm. TUHH Heinrich Voss Tikhonov Regularization for TLS Bremen 2011 4 / 24 Total Least Squares Problems Total Least Squares Problems cnt. Although the name “total least squares” was introduced only recently in the literature by Golub and Van Loan (1980), this fitting method is not new and has a long history in the statistical literature, where it is known as orthogonal regression, errors-in-variables, or measurement errors, and in image deblurring blind deconvolution The univariate problem (n = 1) is already discussed by Adcock (1877), and it was rediscovered many times, often independently. About 30 – 40 years ago, the technique was extended by Sprent (1969) and Gleser (1981) to the multivariate case (n > 1). More recently, the total least squares method also stimulated interest outside statistics. In numerical linear algebra it was first studied by Golub and Van Loan (1980). TUHH Heinrich Voss Tikhonov Regularization for TLS Bremen 2011 5 / 24 Total Least Squares Problems Total Least Squares Problems cnt. Although the name “total least squares” was introduced only recently in the literature by Golub and Van Loan (1980), this fitting method is not new and has a long history in the statistical literature, where it is known as orthogonal regression, errors-in-variables, or measurement errors, and in image deblurring blind deconvolution The univariate problem (n = 1) is already discussed by Adcock (1877), and it was rediscovered many times, often independently. About 30 – 40 years ago, the technique was extended by Sprent (1969) and Gleser (1981) to the multivariate case (n > 1). More recently, the total least squares method also stimulated interest outside statistics. In numerical linear algebra it was first studied by Golub and Van Loan (1980). TUHH Heinrich Voss Tikhonov Regularization for TLS Bremen 2011 5 / 24 Total Least Squares Problems Total Least Squares Problems cnt. Although the name “total least squares” was introduced only recently in the literature by Golub and Van Loan (1980), this fitting method is not new and has a long history in the statistical literature, where it is known as orthogonal regression, errors-in-variables, or measurement errors, and in image deblurring blind deconvolution The univariate problem (n = 1) is already discussed by Adcock (1877), and it was rediscovered many times, often independently. About 30 – 40 years ago, the technique was extended by Sprent (1969) and Gleser (1981) to the multivariate case (n > 1). More recently, the total least squares method also stimulated interest outside statistics. In numerical linear algebra it was first studied by Golub and Van Loan (1980). TUHH Heinrich Voss Tikhonov Regularization for TLS Bremen 2011 5 / 24 Total Least Squares Problems Total Least Squares Problems cnt. Although the name “total least squares” was introduced only recently in the literature by Golub and Van Loan (1980), this fitting method is not new and has a long history in the statistical literature, where it is known as orthogonal regression, errors-in-variables, or measurement errors, and in image deblurring blind deconvolution The univariate problem (n = 1) is already discussed by Adcock (1877), and it was rediscovered many times, often independently. About 30 – 40 years ago, the technique was extended by Sprent (1969) and Gleser (1981) to the multivariate case (n > 1). More recently, the total least squares method also stimulated interest outside statistics. In numerical linear algebra it was first studied by Golub and Van Loan (1980). TUHH Heinrich Voss Tikhonov Regularization for TLS Bremen 2011 5 / 24 Total Least Squares Problems Total Least Squares Problems cnt. The TLS problem can be analyzed in terms of the singular value decomposition of the augmented matrix [A, b] = UΣV T . A TLS solution exists if and only if the right singular subspace Vmin corresponding to σn+1 contains at least one vector with a nonzero last component. It is unique if it holds that σn0 > σn+1 where σn0 denotes the smallest singular value of A, and then it is given by xTLS = − TUHH Heinrich Voss 1 V (1 : n, n + 1). V (n + 1, n + 1) Tikhonov Regularization for TLS Bremen 2011 6 / 24 Total Least Squares Problems Total Least Squares Problems cnt. The TLS problem can be analyzed in terms of the singular value decomposition of the augmented matrix [A, b] = UΣV T . A TLS solution exists if and only if the right singular subspace Vmin corresponding to σn+1 contains at least one vector with a nonzero last component. It is unique if it holds that σn0 > σn+1 where σn0 denotes the smallest singular value of A, and then it is given by xTLS = − TUHH Heinrich Voss 1 V (1 : n, n + 1). V (n + 1, n + 1) Tikhonov Regularization for TLS Bremen 2011 6 / 24 Total Least Squares Problems Total Least Squares Problems cnt. The TLS problem can be analyzed in terms of the singular value decomposition of the augmented matrix [A, b] = UΣV T . A TLS solution exists if and only if the right singular subspace Vmin corresponding to σn+1 contains at least one vector with a nonzero last component. It is unique if it holds that σn0 > σn+1 where σn0 denotes the smallest singular value of A, and then it is given by xTLS = − TUHH Heinrich Voss 1 V (1 : n, n + 1). V (n + 1, n + 1) Tikhonov Regularization for TLS Bremen 2011 6 / 24 Regularization of TLS Problems Outline 1 Total Least Squares Problems 2 Regularization of TLS Problems 3 Tikhonov Regularization of TLS problems 4 Numerical Experiments 5 Conclusions TUHH Heinrich Voss Tikhonov Regularization for TLS Bremen 2011 7 / 24 Regularization of TLS Problems Regularization of TLS Problems When solving practical problems they are usually ill-conditioned, and regularization is necessary to stabilize the computed solution. Fierro, Golub, Hansen and O’Leary (1997) suggested to filter its solution by truncating the small singular values of the TLS matrix [A, b], and they proposed an iterative algorithm based on Lanczos bidiagonalization for computing truncated TLS solutions. TUHH Heinrich Voss Tikhonov Regularization for TLS Bremen 2011 8 / 24 Regularization of TLS Problems Regularization of TLS Problems When solving practical problems they are usually ill-conditioned, and regularization is necessary to stabilize the computed solution. Fierro, Golub, Hansen and O’Leary (1997) suggested to filter its solution by truncating the small singular values of the TLS matrix [A, b], and they proposed an iterative algorithm based on Lanczos bidiagonalization for computing truncated TLS solutions. TUHH Heinrich Voss Tikhonov Regularization for TLS Bremen 2011 8 / 24 Regularization of TLS Problems Regularization Adding a Quadratic Constraint Sima, van Huffel, and Golub (2004) suggest to regularize the TLS problem adding a quadratic constraint k[∆A, ∆b]k2F = min! subject to (A + ∆A)x = b + ∆b, kLxk ≤ δ, where δ > 0 and the regularization matrix L ∈ Rp×n , p ≤ n defines a (semi-) norm on the solution through which the size of the solution is bounded or a certain degree of smoothness can be imposed. Let F ∈ Rn×k be a matrix whose columns form an orthonormal basis of the nullspace of the regularization matrix L. If it holds that σmin ([AF , b]) < σmin (AF ) then the solution xRTLS of the constrained TLS problem is attained (Beck, Ben Tal 2006) TUHH Heinrich Voss Tikhonov Regularization for TLS Bremen 2011 9 / 24 Regularization of TLS Problems Regularization Adding a Quadratic Constraint Sima, van Huffel, and Golub (2004) suggest to regularize the TLS problem adding a quadratic constraint k[∆A, ∆b]k2F = min! subject to (A + ∆A)x = b + ∆b, kLxk ≤ δ, where δ > 0 and the regularization matrix L ∈ Rp×n , p ≤ n defines a (semi-) norm on the solution through which the size of the solution is bounded or a certain degree of smoothness can be imposed. Let F ∈ Rn×k be a matrix whose columns form an orthonormal basis of the nullspace of the regularization matrix L. If it holds that σmin ([AF , b]) < σmin (AF ) then the solution xRTLS of the constrained TLS problem is attained (Beck, Ben Tal 2006) TUHH Heinrich Voss Tikhonov Regularization for TLS Bremen 2011 9 / 24 Regularization of TLS Problems First Order Conditions; Golub, Hansen, O’Leary 1999 Assume xRTLS exists and constraint is active, then (RTLS) is equivalent to f (x) := kAx − bk2 = min! 1 + kxk2 subject to kLxk2 = δ 2 . First-order optimality conditions are equivalent to (AT A + λI I + λL LT L)x µ ≥ 0, 2 kLxk = AT b, = δ2 with λI = − TUHH kAx − bk2 , 1 + kxk2 Heinrich Voss λL = µ(1 + kxk2 ), Tikhonov Regularization for TLS µ= bT (b − Ax) + λI . δ 2 (1 + kxk2 ) Bremen 2011 10 / 24 Regularization of TLS Problems First Order Conditions; Golub, Hansen, O’Leary 1999 Assume xRTLS exists and constraint is active, then (RTLS) is equivalent to f (x) := kAx − bk2 = min! 1 + kxk2 subject to kLxk2 = δ 2 . First-order optimality conditions are equivalent to (AT A + λI I + λL LT L)x µ ≥ 0, 2 kLxk = AT b, = δ2 with λI = − TUHH kAx − bk2 , 1 + kxk2 Heinrich Voss λL = µ(1 + kxk2 ), Tikhonov Regularization for TLS µ= bT (b − Ax) + λI . δ 2 (1 + kxk2 ) Bremen 2011 10 / 24 Regularization of TLS Problems Two Iterative Algorithms based on EVPs Two approaches for solving the first order conditions AT A + λI (x)I + λL (x)LT L x = AT b (∗) 1. Quadratic EVPs: Sima, Van Huffel, Golub (2004), Lampe, V. (2007,2008) Iterative algorithm based on updating λI With fixed λI reformulate (∗) into QEP Determine rightmost eigenvalue, i.e. the free parameter λL Use corresponding eigenvector to update λI 2. Linear EVPs: Renaut, Guo (2005), Lampe, V. (2008) Iterative algorithm based on updating λL With fixed λL reformulate (∗) into linear EVP Determine smallest eigenvalue, i.e. the free parameter λI Use corresponding eigenvector to update λL TUHH Heinrich Voss Tikhonov Regularization for TLS Bremen 2011 11 / 24 Regularization of TLS Problems Two Iterative Algorithms based on EVPs Two approaches for solving the first order conditions AT A + λI (x)I + λL (x)LT L x = AT b (∗) 1. Quadratic EVPs: Sima, Van Huffel, Golub (2004), Lampe, V. (2007,2008) Iterative algorithm based on updating λI With fixed λI reformulate (∗) into QEP Determine rightmost eigenvalue, i.e. the free parameter λL Use corresponding eigenvector to update λI 2. Linear EVPs: Renaut, Guo (2005), Lampe, V. (2008) Iterative algorithm based on updating λL With fixed λL reformulate (∗) into linear EVP Determine smallest eigenvalue, i.e. the free parameter λI Use corresponding eigenvector to update λL TUHH Heinrich Voss Tikhonov Regularization for TLS Bremen 2011 11 / 24 Regularization of TLS Problems Two Iterative Algorithms based on EVPs Two approaches for solving the first order conditions AT A + λI (x)I + λL (x)LT L x = AT b (∗) 1. Quadratic EVPs: Sima, Van Huffel, Golub (2004), Lampe, V. (2007,2008) Iterative algorithm based on updating λI With fixed λI reformulate (∗) into QEP Determine rightmost eigenvalue, i.e. the free parameter λL Use corresponding eigenvector to update λI 2. Linear EVPs: Renaut, Guo (2005), Lampe, V. (2008) Iterative algorithm based on updating λL With fixed λL reformulate (∗) into linear EVP Determine smallest eigenvalue, i.e. the free parameter λI Use corresponding eigenvector to update λL TUHH Heinrich Voss Tikhonov Regularization for TLS Bremen 2011 11 / 24 Tikhonov Regularization of TLS problems Outline 1 Total Least Squares Problems 2 Regularization of TLS Problems 3 Tikhonov Regularization of TLS problems 4 Numerical Experiments 5 Conclusions TUHH Heinrich Voss Tikhonov Regularization for TLS Bremen 2011 12 / 24 Tikhonov Regularization of TLS problems Tikhonov Regularization of TLS problem f (x) + λkLxk2 = kAx − bk2 + λkLxk2 = min!. 1 + kxk2 Beck, Ben–Tal (2006) proposed an algorithm where in each iteration step a Cholesky decomposition has to be computed, which is prohibitive for large-scale problems. We present a method which solves the first order conditions which are equivalent to q(x) := (AT A + µLT L − f (x)I)x − AT b = 0, with µ := (1 + kxk2 )λ. via a combination of Newton’s method with an iterative projection method. TUHH Heinrich Voss Tikhonov Regularization for TLS Bremen 2011 13 / 24 Tikhonov Regularization of TLS problems Tikhonov Regularization of TLS problem f (x) + λkLxk2 = kAx − bk2 + λkLxk2 = min!. 1 + kxk2 Beck, Ben–Tal (2006) proposed an algorithm where in each iteration step a Cholesky decomposition has to be computed, which is prohibitive for large-scale problems. We present a method which solves the first order conditions which are equivalent to q(x) := (AT A + µLT L − f (x)I)x − AT b = 0, with µ := (1 + kxk2 )λ. via a combination of Newton’s method with an iterative projection method. TUHH Heinrich Voss Tikhonov Regularization for TLS Bremen 2011 13 / 24 Tikhonov Regularization of TLS problems Tikhonov Regularization of TLS problem f (x) + λkLxk2 = kAx − bk2 + λkLxk2 = min!. 1 + kxk2 Beck, Ben–Tal (2006) proposed an algorithm where in each iteration step a Cholesky decomposition has to be computed, which is prohibitive for large-scale problems. We present a method which solves the first order conditions which are equivalent to q(x) := (AT A + µLT L − f (x)I)x − AT b = 0, with µ := (1 + kxk2 )λ. via a combination of Newton’s method with an iterative projection method. TUHH Heinrich Voss Tikhonov Regularization for TLS Bremen 2011 13 / 24 Tikhonov Regularization of TLS problems Tikhonov Regularization of TLS problem Newton’s method: x k +1 = x k − J(x k )−1 q(x k ) with the Jacobi matrix J(x) = AT A + µLT L − f (x)I − 2x x T AT A − bT A − f (x)x T . 1 + kxk2 Sherman–Morrison formula yields x k+1 = Ĵk−1 AT b − 1 1− (v k )T Ĵk−1 u k Ĵk−1 u k (v k )T (x k − Ĵk−1 AT b), with Ĵ(x) := AT A + µLT L − f (x)I, u k := 2x k /(1 + kx k k2 ) and v k := AT Ax k − AT b − f (x k )x k . TUHH Heinrich Voss Tikhonov Regularization for TLS Bremen 2011 14 / 24 Tikhonov Regularization of TLS problems Tikhonov Regularization of TLS problem Newton’s method: x k +1 = x k − J(x k )−1 q(x k ) with the Jacobi matrix J(x) = AT A + µLT L − f (x)I − 2x x T AT A − bT A − f (x)x T . 1 + kxk2 Sherman–Morrison formula yields x k+1 = Ĵk−1 AT b − 1 1− (v k )T Ĵk−1 u k Ĵk−1 u k (v k )T (x k − Ĵk−1 AT b), with Ĵ(x) := AT A + µLT L − f (x)I, u k := 2x k /(1 + kx k k2 ) and v k := AT Ax k − AT b − f (x k )x k . TUHH Heinrich Voss Tikhonov Regularization for TLS Bremen 2011 14 / 24 Tikhonov Regularization of TLS problems Tikhonov Regularization of TLS problem To avoid the solution of the large scale linear systems with varying matrices Ĵk we combine Newton’s method with an iterative projection method. Let V be an ansatz space of small dimension k , and let the columns of V ∈ Rk ×n form an orthonormal basis of V. Replace z = Ĵk−1 AT b with Vy1k where y1k solves V T Ĵk Vy1k = AT b, and w = Ĵk−1 u k with Vy2k where y2k solves V T Ĵk Vy2k = u k . If xk+1 = Vk y1k − 1 1− (v k )T Vk y2k Vk y2k (v k )T (x k − Vk y1k ) does not satisfy a prescribed accuracy requirement, then V is expanded with the residual q(x k+1 ) = (AT A + µLT L − f (x k )I)x k+1 − AT b and the step is repeated until convergence. TUHH Heinrich Voss Tikhonov Regularization for TLS Bremen 2011 15 / 24 Tikhonov Regularization of TLS problems Tikhonov Regularization of TLS problem To avoid the solution of the large scale linear systems with varying matrices Ĵk we combine Newton’s method with an iterative projection method. Let V be an ansatz space of small dimension k , and let the columns of V ∈ Rk ×n form an orthonormal basis of V. Replace z = Ĵk−1 AT b with Vy1k where y1k solves V T Ĵk Vy1k = AT b, and w = Ĵk−1 u k with Vy2k where y2k solves V T Ĵk Vy2k = u k . If xk+1 = Vk y1k − 1 1− (v k )T Vk y2k Vk y2k (v k )T (x k − Vk y1k ) does not satisfy a prescribed accuracy requirement, then V is expanded with the residual q(x k+1 ) = (AT A + µLT L − f (x k )I)x k+1 − AT b and the step is repeated until convergence. TUHH Heinrich Voss Tikhonov Regularization for TLS Bremen 2011 15 / 24 Tikhonov Regularization of TLS problems Tikhonov Regularization of TLS problem To avoid the solution of the large scale linear systems with varying matrices Ĵk we combine Newton’s method with an iterative projection method. Let V be an ansatz space of small dimension k , and let the columns of V ∈ Rk ×n form an orthonormal basis of V. Replace z = Ĵk−1 AT b with Vy1k where y1k solves V T Ĵk Vy1k = AT b, and w = Ĵk−1 u k with Vy2k where y2k solves V T Ĵk Vy2k = u k . If xk+1 = Vk y1k − 1 1− (v k )T Vk y2k Vk y2k (v k )T (x k − Vk y1k ) does not satisfy a prescribed accuracy requirement, then V is expanded with the residual q(x k+1 ) = (AT A + µLT L − f (x k )I)x k+1 − AT b and the step is repeated until convergence. TUHH Heinrich Voss Tikhonov Regularization for TLS Bremen 2011 15 / 24 Tikhonov Regularization of TLS problems Tikhonov Regularization of TLS problem Initializing the iterative projection method with a Krylov space V = K` (AT A + µLT L, AT b) the iterates x k are contained in a Krylov space of AT A + µLT L. Due to the convergence properties of the Lanczos process the main √ contributions come from the first singular vectors of [A; µL] which for small µ are close to the first right singular vectors of A. It is common knowledge that these vectors are not always appropriate basis vectors for a regularized solution, and it may be advantageous to apply the regularization with a general regularization matrix L implicitly. TUHH Heinrich Voss Tikhonov Regularization for TLS Bremen 2011 16 / 24 Tikhonov Regularization of TLS problems Tikhonov Regularization of TLS problem Initializing the iterative projection method with a Krylov space V = K` (AT A + µLT L, AT b) the iterates x k are contained in a Krylov space of AT A + µLT L. Due to the convergence properties of the Lanczos process the main √ contributions come from the first singular vectors of [A; µL] which for small µ are close to the first right singular vectors of A. It is common knowledge that these vectors are not always appropriate basis vectors for a regularized solution, and it may be advantageous to apply the regularization with a general regularization matrix L implicitly. TUHH Heinrich Voss Tikhonov Regularization for TLS Bremen 2011 16 / 24 Tikhonov Regularization of TLS problems Tikhonov Regularization of TLS problem Initializing the iterative projection method with a Krylov space V = K` (AT A + µLT L, AT b) the iterates x k are contained in a Krylov space of AT A + µLT L. Due to the convergence properties of the Lanczos process the main √ contributions come from the first singular vectors of [A; µL] which for small µ are close to the first right singular vectors of A. It is common knowledge that these vectors are not always appropriate basis vectors for a regularized solution, and it may be advantageous to apply the regularization with a general regularization matrix L implicitly. TUHH Heinrich Voss Tikhonov Regularization for TLS Bremen 2011 16 / 24 Tikhonov Regularization of TLS problems Tikhonov Regularization of TLS problem Assume that L is nonsingular and use the transformation x := L−1 y (for general L we had to use the A-weighted generalized inverse L†A , cf. Elden 1982) which yields kAL−1 y − bk2 + λky k2 = min!. 1 + kL−1 y k2 Transforming the first order conditions back and multiplying from the left with L−1 one gets (LT L)−1 (AT Ax + µLT Lx − f (x)x − AT b) = 0. This equation suggests to precondition the expansion of the search space with LT L or an approximation M ≈ LT L thereof which yields the following Algorithm. TUHH Heinrich Voss Tikhonov Regularization for TLS Bremen 2011 17 / 24 Tikhonov Regularization of TLS problems Tikhonov Regularization of TLS problem Assume that L is nonsingular and use the transformation x := L−1 y (for general L we had to use the A-weighted generalized inverse L†A , cf. Elden 1982) which yields kAL−1 y − bk2 + λky k2 = min!. 1 + kL−1 y k2 Transforming the first order conditions back and multiplying from the left with L−1 one gets (LT L)−1 (AT Ax + µLT Lx − f (x)x − AT b) = 0. This equation suggests to precondition the expansion of the search space with LT L or an approximation M ≈ LT L thereof which yields the following Algorithm. TUHH Heinrich Voss Tikhonov Regularization for TLS Bremen 2011 17 / 24 Tikhonov Regularization of TLS problems Tikhonov Regularization of TLS problem Assume that L is nonsingular and use the transformation x := L−1 y (for general L we had to use the A-weighted generalized inverse L†A , cf. Elden 1982) which yields kAL−1 y − bk2 + λky k2 = min!. 1 + kL−1 y k2 Transforming the first order conditions back and multiplying from the left with L−1 one gets (LT L)−1 (AT Ax + µLT Lx − f (x)x − AT b) = 0. This equation suggests to precondition the expansion of the search space with LT L or an approximation M ≈ LT L thereof which yields the following Algorithm. TUHH Heinrich Voss Tikhonov Regularization for TLS Bremen 2011 17 / 24 Tikhonov Regularization of TLS problems Tikhonov Regularization of TLS problem Require: Initial basis V0 with V0T V0 = I, starting vector x 0 1: for k = 0, 1, . . . until convergence do 2: Compute f (x k ) = kAx k − bk2 /(1 + kx k k2 ) 3: Solve VkT Ĵk Vk y1k = VkT AT b for y1k 4: Compute u k = 2x k /(1 + kx k k2 ) and v k = AT Ax k − AT b − f (x k )x k 5: Solve VkT Ĵk Vk y2k = VkT u k for y2k 6: Compute x k +1 = Vk y1k − 1−(v k1)T V y k Vk y2k (v k )T (x k − Vk y1k ) k 2 7: 8: 9: 10: 11: 12: 13: TUHH Compute q k+1 = (AT A + µLT L − f (x k )I)x k+1 − AT b Compute r̃ = M −1 q k +1 Orthogonalize r̂ = (I − Vk VkT )r̃ Normalize vnew = r̂ /kr̂ k Enlarge search space Vk+1 = [Vk , vnew ] end for Output: Approximate Tikhonov TLS solution x k+1 Heinrich Voss Tikhonov Regularization for TLS Bremen 2011 18 / 24 Tikhonov Regularization of TLS problems Tikhonov Regularization of TLS problem The Tikhonov TLS methods allows for a massive reuse of information from previous iteration steps. Assume that the matrices Vk , AT AVk , LT LVk are stored. Then neglecting multiplications with L and LT and solves with M the essential cost in every iteration step is only two matrix-vector products with dense matrices A and AT for extending AT AVk . With these matrices f (x k ) in Line 1 can be evaluated as 1 T 2 k T T k k T T , f (x k ) = (x ) (A Ay ) − 2(y ) V (A b) + kbk k 1 + ky k k2 and q k+1 in Line 7 can be determined according to q k+1 = (AT AVk )y k +1 + µ(LT LVk )y k +1 − f (x k )x k+1 − AT b. Since the the number of iteration steps until convergence is usually very small compared to the dimension n, the overall cost of the Algorithm is of the order O(mn). TUHH Heinrich Voss Tikhonov Regularization for TLS Bremen 2011 19 / 24 Tikhonov Regularization of TLS problems Tikhonov Regularization of TLS problem The Tikhonov TLS methods allows for a massive reuse of information from previous iteration steps. Assume that the matrices Vk , AT AVk , LT LVk are stored. Then neglecting multiplications with L and LT and solves with M the essential cost in every iteration step is only two matrix-vector products with dense matrices A and AT for extending AT AVk . With these matrices f (x k ) in Line 1 can be evaluated as 1 T 2 k T T k k T T , f (x k ) = (x ) (A Ay ) − 2(y ) V (A b) + kbk k 1 + ky k k2 and q k+1 in Line 7 can be determined according to q k+1 = (AT AVk )y k +1 + µ(LT LVk )y k +1 − f (x k )x k+1 − AT b. Since the the number of iteration steps until convergence is usually very small compared to the dimension n, the overall cost of the Algorithm is of the order O(mn). TUHH Heinrich Voss Tikhonov Regularization for TLS Bremen 2011 19 / 24 Tikhonov Regularization of TLS problems Tikhonov Regularization of TLS problem The Tikhonov TLS methods allows for a massive reuse of information from previous iteration steps. Assume that the matrices Vk , AT AVk , LT LVk are stored. Then neglecting multiplications with L and LT and solves with M the essential cost in every iteration step is only two matrix-vector products with dense matrices A and AT for extending AT AVk . With these matrices f (x k ) in Line 1 can be evaluated as 1 T 2 k T T k k T T , f (x k ) = (x ) (A Ay ) − 2(y ) V (A b) + kbk k 1 + ky k k2 and q k+1 in Line 7 can be determined according to q k+1 = (AT AVk )y k +1 + µ(LT LVk )y k +1 − f (x k )x k+1 − AT b. Since the the number of iteration steps until convergence is usually very small compared to the dimension n, the overall cost of the Algorithm is of the order O(mn). TUHH Heinrich Voss Tikhonov Regularization for TLS Bremen 2011 19 / 24 Tikhonov Regularization of TLS problems Tikhonov Regularization of TLS problem The Tikhonov TLS methods allows for a massive reuse of information from previous iteration steps. Assume that the matrices Vk , AT AVk , LT LVk are stored. Then neglecting multiplications with L and LT and solves with M the essential cost in every iteration step is only two matrix-vector products with dense matrices A and AT for extending AT AVk . With these matrices f (x k ) in Line 1 can be evaluated as 1 T 2 k T T k k T T , f (x k ) = (x ) (A Ay ) − 2(y ) V (A b) + kbk k 1 + ky k k2 and q k+1 in Line 7 can be determined according to q k+1 = (AT AVk )y k +1 + µ(LT LVk )y k +1 − f (x k )x k+1 − AT b. Since the the number of iteration steps until convergence is usually very small compared to the dimension n, the overall cost of the Algorithm is of the order O(mn). TUHH Heinrich Voss Tikhonov Regularization for TLS Bremen 2011 19 / 24 Numerical Experiments Outline 1 Total Least Squares Problems 2 Regularization of TLS Problems 3 Tikhonov Regularization of TLS problems 4 Numerical Experiments 5 Conclusions TUHH Heinrich Voss Tikhonov Regularization for TLS Bremen 2011 20 / 24 Numerical Experiments Numerical Experiments Consider several examples from Hansen’s Regularization Tools. The regularization matrix L is chosen to be the nonsingular approximation to the scaled discrete first order derivative operator in one space-dimension. The numerical tests are carried out on an Intel Core 2 Duo T7200 computer with 2.3 GHz and 2 GB RAM under MATLAB R2009a (actually our numerical examples require less than 0.5 GB RAM). TUHH Heinrich Voss Tikhonov Regularization for TLS Bremen 2011 21 / 24 Numerical Experiments Numerical Experiments Consider several examples from Hansen’s Regularization Tools. The regularization matrix L is chosen to be the nonsingular approximation to the scaled discrete first order derivative operator in one space-dimension. The numerical tests are carried out on an Intel Core 2 Duo T7200 computer with 2.3 GHz and 2 GB RAM under MATLAB R2009a (actually our numerical examples require less than 0.5 GB RAM). TUHH Heinrich Voss Tikhonov Regularization for TLS Bremen 2011 21 / 24 Numerical Experiments Numerical Experiments Consider several examples from Hansen’s Regularization Tools. The regularization matrix L is chosen to be the nonsingular approximation to the scaled discrete first order derivative operator in one space-dimension. The numerical tests are carried out on an Intel Core 2 Duo T7200 computer with 2.3 GHz and 2 GB RAM under MATLAB R2009a (actually our numerical examples require less than 0.5 GB RAM). TUHH Heinrich Voss Tikhonov Regularization for TLS Bremen 2011 21 / 24 Numerical Experiments Numerical Experiments Problem phillips σ = 1e − 3 baart σ = 1e − 3 shaw σ = 1e − 3 deriv2 σ = 1e − 3 heat(κ=1) σ = 1e − 2 heat(κ=5) σ = 1e − 3 TUHH Method kq(x k )k kAT bk Iters MatVecs kx−xtrue k kxtrue k TTLS RTLSQEP RTLSEVP TTLS RTLSQEP RTLSEVP TTLS RTLSQEP RTLSEVP TTLS RTLSQEP RTLSEVP TTLS RTLSQEP RTLSEVP TTLS RTLSQEP RTLSEVP 8.5e-16 5.7e-11 7.1e-13 2.3e-15 1.0e-07 4.1e-10 9.6e-16 3.7e-09 2.6e-10 1.2e-15 2.3e-09 2.6e-12 8.4e-16 4.1e-08 3.2e-11 1.4e-13 6.1e-07 9.8e-11 8.0 3.0 4.0 10.1 15.7 7.8 8.3 4.1 3.0 10.0 3.1 5.0 19.9 3.8 4.1 25.0 4.6 4.0 25.0 42.0 47.6 29.2 182.1 45.6 25.6 76.1 39.0 29.0 52.3 67.0 48.8 89.6 67.2 59.0 105.2 65.0 8.9e-2 8.9e-2 8.9e-2 1.5e-1 1.4e-1 1.5e-1 7.0e-2 7.0e-2 7.0e-2 4.9e-2 4.9e-2 4.9e-2 1.5e-1 1.5e-1 1.5e-1 1.1e-1 1.1e-1 1.1e-1 Heinrich Voss Tikhonov Regularization for TLS Bremen 2011 22 / 24 Conclusions Outline 1 Total Least Squares Problems 2 Regularization of TLS Problems 3 Tikhonov Regularization of TLS problems 4 Numerical Experiments 5 Conclusions TUHH Heinrich Voss Tikhonov Regularization for TLS Bremen 2011 23 / 24 Conclusions Conclusions We discussed a Tikhonov regularization approach for large total least squares problems. It is highly advantageous to combine Newton’s method with an iterative projection method and to reuse information gathered in previous iteration steps. Several examples demonstrate that fairly small ansatz spaces are are sufficient to get accurate solutions. Hence, the method is qualified to solve large-scale regularized total least squares problems efficiently We assumed the regularization parameter λ to be fixed. The same technique of recycling ansatz spaces can be used in an L-curve method to determine a reasonable parameter. TUHH Heinrich Voss Tikhonov Regularization for TLS Bremen 2011 24 / 24 Conclusions Conclusions We discussed a Tikhonov regularization approach for large total least squares problems. It is highly advantageous to combine Newton’s method with an iterative projection method and to reuse information gathered in previous iteration steps. Several examples demonstrate that fairly small ansatz spaces are are sufficient to get accurate solutions. Hence, the method is qualified to solve large-scale regularized total least squares problems efficiently We assumed the regularization parameter λ to be fixed. The same technique of recycling ansatz spaces can be used in an L-curve method to determine a reasonable parameter. TUHH Heinrich Voss Tikhonov Regularization for TLS Bremen 2011 24 / 24 Conclusions Conclusions We discussed a Tikhonov regularization approach for large total least squares problems. It is highly advantageous to combine Newton’s method with an iterative projection method and to reuse information gathered in previous iteration steps. Several examples demonstrate that fairly small ansatz spaces are are sufficient to get accurate solutions. Hence, the method is qualified to solve large-scale regularized total least squares problems efficiently We assumed the regularization parameter λ to be fixed. The same technique of recycling ansatz spaces can be used in an L-curve method to determine a reasonable parameter. TUHH Heinrich Voss Tikhonov Regularization for TLS Bremen 2011 24 / 24 Conclusions Conclusions We discussed a Tikhonov regularization approach for large total least squares problems. It is highly advantageous to combine Newton’s method with an iterative projection method and to reuse information gathered in previous iteration steps. Several examples demonstrate that fairly small ansatz spaces are are sufficient to get accurate solutions. Hence, the method is qualified to solve large-scale regularized total least squares problems efficiently We assumed the regularization parameter λ to be fixed. The same technique of recycling ansatz spaces can be used in an L-curve method to determine a reasonable parameter. TUHH Heinrich Voss Tikhonov Regularization for TLS Bremen 2011 24 / 24