Download Measuring Matter

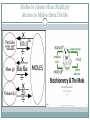
Measuring Matter
THE MOLE
(NO, NOT HIM)
The Mole
 Chemists use the mole to count atoms, molecules,
ions and formula units.
 SI unit = mol
 mol = 6.0221367 x 1023
 This is known as Avogadro’s number
Extra Credit: Who was Avogadro? 5points
on next quiz. Write it down. What did he
do? Where was he from? Why did they
name this number after him?
Converting between Moles and Particles
 Suppose you buy 3 ½ dozens of roses and want to
know how many roses you have.

1 dozen roses = 12 roses

3.5 dozen roses x
12 𝑟𝑜𝑠𝑒𝑠
1 𝑑𝑜𝑧𝑒𝑛 𝑟𝑜𝑠𝑒𝑠
 1 mol = 6.02 x 1023
 Pg. 323 practice #1-4
 Pg. 324 practice #5-6
= ? Roses
Moles to Atoms then Multiply
Atoms to Moles then Divide
Moles to Atoms
multiply
 How many atoms of Zn are there in 2.5 mol of Zn?
 Set up problem as a proportion problem
 2.5 mol Zn x

6.02 𝑥 1023 𝑎𝑡𝑜𝑚𝑠 𝑜𝑓 𝑍𝑛
1 𝑚𝑜𝑙
Treat the proportion like 2 math problems
 (2.5 x 6.03) x 1023
23
 Multiply the whole numbers and bring down x 10
 15.05 x 1023
 Move decimal to proper place and change the exponent
 1.51 x 1024 atoms Zn
Practice problems Page 323
 Zinc is used to galvanize steel. Determine the
number of Zn atoms are in 2.50 mol of Zn.
 Calculate the number of molecules in 11.5 mol water.
 Silver nitrate is used to make different silver halides
for photographic films. How many formula units of
silver nitrate are in 3.25 mol of silver nitrate?
 Calculate the number of oxygen atoms in 5.0 mol of
oxygen molecules. Remember oxygen is a diatomic
molecule.
Atoms to Moles
divide
 How many moles are in 5.75 𝑥 1024 atoms Al ?
 Set up problem as a proportion problem
5.75 𝑥 1024

1

Treat the proportion like 2 math problems
5.75

6.02

x
1 𝑚𝑜𝑙
6.02 𝑥 1023
x
1024
1023
Divide whole numbers then subtract the exponents
 0.95 x 1024−23
 Move decimal to proper place and change the exponent
 9.5 x 101−1 = 9.5 x 100 = 9.5 moles Al
Practice problems page 324
 Calculate the number of moles of zinc that contain
4.5 x 1024 atoms.
 How many moles contain each of the following?


5.75 x 1024 atoms Al
2.50 x 1020 atoms of iron
 Identify the particle for each formula and convert the
given number of representative particles to moles:


3.75 x 1024 𝐶𝑂2
3.58 x 1023 𝑍𝑛𝐶𝑙2
Ch. 10 sect. 1 Assessment
 Explain why chemists use the mole
 State the mathematical relationship between Avogadro’s





number and 1 mol.
List the conversion factors used to convert between
particles and moles.
Explain how a mole is similar to a dozen.
How does a chemist count the number of particles in a
given number of mole of a substance?
Calculate the mass in atomic mass units of 0.25 mol of
carbon-12 atoms.
Calculate the number of representative particles of each
substance:


11.5 mol Ag
18.0 mol water
0.150 mol NaCl
1.35 x 10−2 mol 𝐶𝐻4
QUIZ Tomorrow
 Remember extra credit opportunity????
 Know what a mole is
 Be able to convert from moles to particles
 Be able to convert from particles to moles
 You may use your foldable ONLY if you have the
acceptable information AND it is your personal
foldable that you made
Mass of a Mole
 A dozen limes does not have the same mass as a
dozen eggs. Why do you suppose that is?
 Composition and size
 The mole is defined as the number of carbon-12
atoms in 12 grams of pure carbon-12. Therefore the
mass of one mole of carbon-12 is 12 grams.
 How does the mass of one atom relate to the mass of
another atom if their size and composition are
different?
Molar Mass
 Although the Eastern ground mole has an average mass of 75 grams, he is not the
topic of our lesson.
 The mass in grams of one mole of any pure
substance is called its molar mass.
 The molar mass of any element is equal to its average
atomic mass.
Molar Mass
 SI units of molar mass = g/mol
 Fe atom has atomic mass of 55.847 amu
 55.847 amu = 55.847 g/mol Fe
 55.847 g/mol Fe = 6.02 x 1023 atoms Fe
 1 mol Fe = 55.847 g. Fe
 So what is the relationship between molar mass,
average atomic mass, grams, and moles of a
substance?
 What is the relationship between molar mass and
number of atoms?
Practice Calculating Molar Mass
Elements:
 Look at the periodic table
 The average atomic mass = molar mass = g/mol
https://www.youtube.com/watch?v=F9NkYSKJifs

What is the molar mass of the following?
Lithium = 𝑀𝐿𝑖 = 6.941 g/mol
 Sulfur =
 Cobalt =
 Sodium =
 Zinc =
 Oxygen =

Practice Calculating Molar Mass
Molecules
 Add up the mass if each element

𝐻2 𝑆𝑂4
There are 2 hydrogen atoms = (2 x 1.01) = 2.02 g/mol
 There is 1 sulfur atom = (1 x 34.39)
= 34.39 g/mol
 There are 4 oxygen atoms = (4 x 15.99) = 63.96 g/mol



Total amount = 𝑀𝐻2𝑆𝑂4 =
What is the molar mass of the following?
Lithium chloride
 Water

Using Molar Mass
 Suppose while working in lab you needed 3.0 mol
Cu for a chemical reaction. How would you measure
the amount needed to create a 3.0 mol Cu solution?

Multiply the number of moles by the molar mass


3.0 mol Cu x
63.55 𝑔 𝐶𝑢
1 𝑚𝑜𝑙 𝐶𝑢
= ? g Cu
Using a weighing boat or weighing paper, place the calculated
number of grams of copper into the boat. Remember to tare
the balance before measuring mass of boat. The amount of
copper must be 191 g more than the mass of the boat.
 Complete practice problems pg. 328 #15-16
Page 328-329
 How many grams are in:
 3.57 mol Al
 42.8 mol Si
2
 3.45 x 10 mol Cu
−2 mol Zn
 2.45 x 10
 How many moles are in:
 25.5 g Ag
 300.0 g S
 How many grams are in:
3
 1.25 x 10 g Zn
 1.00 kg Fe
Using Molar Mass
 Suppose you are given 525 g of Calcium. For this lab
create a solution and write the molarity of the
solution on the solution flask. How will you calculate
the molarity if given the mass?

Divide the mass given by the molar mass to find molarity of
the solution.


525 g Ca x
1 𝑚𝑜𝑙 𝐶𝑎
40.08 𝑔 𝐶𝑎
= ? mol Ca
After checking the amount of calcium and properly mixing the
solution according to directions, you can label the flask 13.1
mol Ca.
 Complete practice problems on pg 329-331..
Practice Using Molar Mass
Now that you know two definitions of a mole (a gram formula weight and an Avogadro’s number of particles)
you can combine these two definitions into one problem.
EXAMPLE: How many molecules are there in 90.1 grams of water?
2 H = 2 x(1.01) = 2.02
O = 1 x (16.00) = 16.00
H2O
= 18.02 g
# molecules H2O = 90.1 g H2O x 1 mole H2O
18.02 g H2O
x 6.02 x 1023 molecules H2O = 3.01 x 1024 molecules H2O
1 mole H2O
EXAMPLE: What would be the mass of 3.01 x 1023 molecules of ammonia (NH3)?
N = 1 x (14.01) = 14.01
3 H = 3 x (1.01) = 3.03
NH3
= 17.04 g
# grams NH3 = 3.01 x 1023 molecules NH3 x 1 mole NH3
x 17.04 g NH3 = 8.52 g NH3
23
6.02 x 10 molecules NH3
1 mole NH3
Practice Problems Page 331
 How many atoms are in:
 55.2 g Li
 0.230 g Pb
 11.5 g Hg
 What is the mass in grams for:
24 atoms Bi
 6.02 x 10
24 atoms Mn
 1.00 x 10
22 atoms He
 3.4 x 10
15 atoms N
 1.5 x 10
Chapter 10 Section 2 Assessment
 Summarize in terms of particles and mass, one-mole quantities of two different




elements
State the conversion factor needed to convert between mass and moles of
atoms of fluorine.
Explain how molar mass relates the mass of an atom to the mass of a mole of
atoms.
Describe the steps used to convert the mass of an element to the number of
atoms in an element.
Arrange these quantities from smallest to largest in terms of mass:



1.0 mol of Ar
3.0 x 1024 atoms of Ne
20 g of Kr
 Identify the quantity that is calculated by dividing the molar mass of an
element by Avogadro’s number
 Design a concept map that shows the conversion factors needed to convert
between mass, moles and number of particles
Calculating Parts of the Whole
 Ever wonder how drug and
food companies know how
much of each compound,
element or mineral is in the
matter we consume/eat?
 How do they know how
much is good for us?
 Why can’t we all take in the
same amount?
 There is a science to it. And
yes, it involves mathematical
calculations.
Lets try this
 Ms. Wildes gives her students bags of M&M candies
and tells them to compare the different colors of
candies. Each group is to create a graph to show
what they have found.
 How would you calculate the percentage of each
color?
 Now it is your turn.
 Using the example from Ms. Wilde’s class and the
bag of M&M’s you have



1. create your own data table based on your bag of M&M’s
2. compare your data with 2 other groups and record their
findings
3. draw a conclusion regarding the percentages
Calculating Parts of the Whole
Ratio
 The relationship in size or quantity of two or more
things
 Proportion
 Examples for 𝐶𝐶𝑙2 𝐹2 :

1 𝑚𝑜𝑙 𝐶 𝑎𝑡𝑜𝑚𝑠
1 𝑚𝑜𝑙𝐶𝐶𝑙2 𝐹2
2 𝑚𝑜𝑙 𝐶𝑙 𝑎𝑡𝑜𝑚𝑠
1 𝑚𝑜𝑙𝐶𝐶𝑙2 𝐹2
2 𝑚𝑜𝑙 𝐹 𝑎𝑡𝑜𝑚𝑠
1 𝑚𝑜𝑙𝐶𝐶𝑙2 𝐹2
Bicarbonate of soda (sodium hydrogen carbonate) is used in many
commercial preparations. Its formula is NaHCO3.
Find the mass percentages (mass %) of Na, H, C, and O in sodium
hydrogen carbonate.
 First, look up the atomic masses for the elements from the
Periodic Table.
Na is 22.99
 H is 1.01
 C is 12.01
 O is 16.00

 Next, determine how many grams of each element are
present in one mole of NaHCO3:

22.99 g (1 mol) of Na
1.01 g (1 mol) of H
12.01 g (1 mol) of C
48.00 g (3 mole x 16.00 gram per mole) of O
 The mass of one mole of NaHCO3 is:
22.99 g + 1.01 g + 12.01 g + 48.00 g = 84.01 g
 And the mass percentages of the elements are

mass % Na = 22.99 g / 84.01 g x 100 = 27.36 %
mass % H = 1.01 g / 84.01 g x 100 = 1.20 %
mass % C = 12.01 g / 84.01 g x 100 = 14.30 %
mass % O = 48.00 g / 84.01 g x 100 = 57.14 %
For each of the following compounds, write out all of the
possible ratios:
 𝑁𝐻4
1 𝑚𝑜𝑙 𝑁

1 𝑚𝑜𝑙𝑁𝐻4
and
4 𝑚𝑜𝑙 𝐻
1 𝑚𝑜𝑙𝑁𝐻4
How will you celebrate?
Are you “counting” the days?
Stiochiometry
 The word stoichiometry derives from two Greek
words: stoicheion (meaning "element") and metron
(meaning "measure").
 Stoichiometry deals with calculations about the
masses (sometimes volumes) of reactants and
products involved in a chemical reaction.
 It is a very mathematical part of chemistry, so be
prepared for lots of calculator use
 The most common stoichiometry problem will
present you with a certain amount of a reactant and
then ask how much of a product can be formed.
 Remember the total mass of reactants will equal the
total mass of the products.
 It is a recipe!
Molar Ratio
 The molar ratio will assume a place of central




importance in solving stoichiometry problems.
The sources for these ratios are the coefficients of a
balanced equation.
2H2 + O2 ---> 2H2O
What is the molar ratio between H2 and O2?
Answer: two-to-one.

This ratio in fractional form is:
 What is the molar ratio between O2 and H2O?
 What is the molar ratio between H2 and H2O?
 Here's another equation: 2O3 ---> 3O2
 The exact molar ratio you would use depends on how the
problem is worded.
 What is the molar ratio between O3 and O2?
 What is the molar ratio between O2 and O3?
 http://www.chemteam.info/Stoichiometry/WS1-
MoleRatio.pdf
Using Molar Ratio
to find how much product is formed
 If we have 2.00 mol of N2 reacting with sufficient H2,
how many moles of NH3 will be produced?

N2 + 3H2 ---> 2NH3
The ratio from the problem will have N2 and NH3 in it.
 Let's use this ratio to set up the proportion:
=
 The ratio from the data in the problem will be:

 The proportion (setting the two ratios equal) is:
 Solving by cross-multiplying
 1x = 4.00 mol of NH3
A few things to remember:
 How do you know which number goes on top or
bottom in the ratios?


Answer: it does not matter, except that you observe the next point
ALL THE TIME.
When making the two ratios, be 100% certain that numbers
are in the same relative positions. For example, if the value
associated with NH3 is in the numerator, then MAKE SURE it
is in both numerators.
 Use the coefficients of the two substances to make
the ratio from the equation.
 Why isn't H2 involved in the problem?

Answer: The word "sufficient" removes it from consideration.
Solve these problems using:
2 H2 + O2 ---> 2 H2O
 1) How many moles of H2O are produced when 5.00
moles of oxygen are used?



Set up ratios
Cross multiply
Divide to solve
 2) If 3.00 moles of H2O are produced, how many
moles of oxygen must be consumed?



Set up ratios
Cross multiply
Divide to solve
Page 378
 Explain why a balanced chemical equation is needed




to solve a stoichiometry.
List the 4 steps used in solving stoichiometry
problems
Describe how a mole ratio is correctly expressed
when it is used to solve a stoichiometry problem
How can you determine the mass of liquid bromine
needed to react completely with a given mass of
magnesium?
How many grams of ammonia is formed if 2.70 h of
hydrogen gas reacts with excess nitrogen?