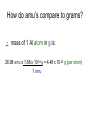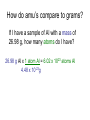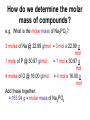* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Moles - tamchemistryhart
Debye–Hückel equation wikipedia , lookup
Isotopic labeling wikipedia , lookup
Crystallization wikipedia , lookup
Rutherford backscattering spectrometry wikipedia , lookup
Size-exclusion chromatography wikipedia , lookup
Mass spectrometry wikipedia , lookup
Molecular dynamics wikipedia , lookup
IUPAC nomenclature of inorganic chemistry 2005 wikipedia , lookup
History of molecular theory wikipedia , lookup
Gas chromatography–mass spectrometry wikipedia , lookup
Moles How can we count how many atoms or molecules are in a piece of matter if we can’t see them? How can we count how many atoms or molecules are in a piece of matter if they have different masses? Moles What can we measure in the laboratory that will help us? What is the “common currency”? MOLES! Moles Unit We will incorporate the following skills and knowledge: • • • • metric system (esp. mass) scientific/exponent notation conversions and dimensional analysis sig figs the most important mathematical tool in chemistry – the mole! Mole 1 mole = the amount of pure substance that contains as many particles (atoms, molecules, or fundamental units) as there are atoms in exactly 12 grams of carbon12 (agreed upon by chemists and physicists in 1960/61) Mole = 6.02 x 1023 particles = Avogadro’s number • Mole comes from molekül (German) = molecule • Molecule comes from molecula (New Latin), meaning very small specimen Background Lorenzo Romano Amedeo Carlo Avogadro (1776-1856) - Italian physics professor 1811 - Avogadro's hypothesis - now a law "Equal volumes of gases under the same conditions have equal numbers of molecules.“ “universal container” Background Late 1800s – chemists – developed scale of relative atomic masses of gases, based on 1/16 of the average atomic mass of oxygen 1920s – physicists – developed relative atomic masses based on 1/16 of the oxygen-16 atom Background 1959-1961 – chemists and physicists agreed to switch to carbon-12 as the standard, setting its atomic mass at 12 (pragmatic reasons – carbon-12 was the standard in mass spectroscopy, and close to chemistry’s oxygen standards) Moles in conversion factors number of “particles” > moles 6.02 x 1023 particles 1 mole mass (g) > moles average atomic mass in g 1 mole Moles in conversion factors number of “particles” > mass (g) both of the above conversion factors, using moles as the intermediate, or “common currency” number of atoms in a compound # atoms 1 compound Math and the Mole (# particles/mole) 1. How many fingers are there on 1 person? 2. How many fingers are there on 1 dozen people? 3. How many fingers are there on 3 dozen people? Math and the Mole (# particles/mole) 4. How many fingers are there on 1 mole of people? 5. How many fingers are there on 3.12 moles of people? Math and the Mole (# particles/mole) 6. How many F atoms in 3.12 moles of F? 7. How many moles of F do you have if you have 2.45 x 1022 atoms of F? Math and the Mole (continued) Hint: If problem includes numbers of atoms or other representative particles and moles, use Avogadro’s number: 6.02 x 1023 particles If problem includes grams and moles use the periodic table to find molar mass. Math and the Mole (continued) (mass/mole) 8.How many grams of F are in 3.89 moles of F? 9.How many moles of F atoms in 45.6 g of F? Math and the Mole (continued) (# particles/mass) 10. How many F atoms are in 65.8 g F? 11. What is the mass, in grams, of 7.62 x 1024 F atoms? Math and the Mole (continued) (# atoms/compound) 12. How many F atoms are in 3.84 moles of MoF6 molecules? A: 1.39 x 1025 F atoms Molar Mass Molar mass = mass, in grams, of 1 mole of a substance (6.02 x 1023 particles) expressed in g/mol Molar mass is numerically equal to average atomic mass in amus (atomic mass units). Molar Mass So, molar mass of oxygen (O) = mass of 1 mole of O atoms = mass of 6.02 x 1023 atoms = 16.00 g/mol molar mass of lead (Pb) = mass of 1 mole of Pb atoms = mass of 6.02 x 1023 atoms = 207.2 g/mol How do amu’s compare to grams? e.g. 1 aluminum atom weighs 26.98 amu. By definition, 1 amu = 1/12 mass of the nucleus of 1 C-12 atom = 1.66 x 10-24 g How do amu’s compare to grams? \ mass of 1 Al atom in g is: 26.98 amu x 1.66 x 10-24 g = 4.48 x 10-23 g (per atom) 1 amu How do amu’s compare to grams? If I have a sample of Al with a mass of 26.98 g, how many atoms do I have? 26.98 g Al x 1 atom Al = 6.02 x 1023 atoms Al 4.48 x 10-23g How do amu’s compare to grams? Or how much does 6.02 x 1023 atoms Al weigh? 4.48 x 10-23 g x 6.02 x 1023 atoms Al = 27.0 g Al atom How do amu’s compare to grams? \ Mass of 1 mole of any element is the “molar mass” of that element. How do we determine the molar mass of compounds? Add up the molar masses of all elements in the compound, taking into account the number of moles of each element. How do we determine the molar mass of compounds? e.g. What is the molar mass of Na3PO4? 3 moles of Na @ 22.99 g/mol = 3 mol x 22.99 g mol 1 mole of P @ 30.97 g/mol = 1 mol x 30.97 g mol 4 moles of O @ 16.00 g/mol = 4 mol x 16.00 g mol Add these together: = 163.94 g = molar mass of Na3PO4 How do we use molar mass of a compound in a conversion problem? The same way we use molar mass of an atom… How do we use molar mass of a compound in a conversion problem? (#atoms/compound and molar mass of compounds) 13. How many Na atoms are in 252 g of Na3PO4? (A: 2.78 x 1024 Na atoms) Where we’ve been (today’s lab quiz; Quiz 6 – next Th/F) • # particles-mole and mole-# particles conversions • mass-mole and mole-mass conversions • # atoms-molecule/formula unit conversion • molar mass of compounds • combination of two or more of above conversions Where we’ve been (today’s lab quiz; Quiz 6 – next Th/F) • Use the sample problems in your notes, Moles WS #1, your bookwork and the warmups to help you prepare for Quiz 6. • Come in for ICP (T/W lunch) for more practice. Where we are going next – applications of mole conversions • % composition by mass from a chemical formula (today) (Moles WS #2) • Find the empirical chemical formula from % composition data (Moles WS #3 & 4) • Find the molecular formula from % composition and empirical formula (Moles WS #4) • Practice problems for all moles material (Moles WS #5) Where we are going next – applications of mole conversions • Calculate molarity of a solution (Moles WS #6 & 7) • Find the mass of a solute or volume of a solution using molarity (Moles WS #6 &7) • Find the mass percent of a solution (Moles WS #7) Calculations relating to Chemical Formulas 1. Determine the molar mass of a compound: - Find molar masses of all elements. - Multiply each mass taking into account the number of atoms of that element present in the formula. - Add all masses together. e.g. What is the molar mass of Pb3(PO4)2? Calculations relating to Chemical Formulas 1. Determine the molar mass of a compound: - Find molar masses of all elements. - Multiply each mass taking into account the number of atoms of that element present in the formula. - Add all masses together. e.g. What is the molar mass of Pb3(PO4)2? 811.5 g/mol Calculations relating to Chemical Formulas 2. Determine percent composition of all elements present in a compound: - Find the molar masses of each element in the compound. - Find the total molar mass. Calculate: % composition = molar mass of element x 100% total molar mass of compound Calculations relating to Chemical Formulas e.g. What is the % composition of NaCl? CaCl2? (assume % composition by mass) Apply % composition: e.g. What mass of Na is present in 200.0 g NaCl? Calculations relating to Chemical Formulas e.g. What is the % composition of NaCl? CaCl2? (assume % composition by mass) NaCl: 39.34% Na, 60.66% Cl CaCl2: 36.11% Ca, 63.89% Cl Apply % composition: e.g. What mass of Na is present in 200.0 g NaCl? 200.0 g x 0.3934 = 78.68 g Na 3. Convert % composition (mass percent) empirical formula a. Assume a 100 g sample – use same numbers as grams rather than %. b. Perform mass mole conversions. c. Divide each result (mole) by the smallest result present (mole ratio). d. Look for whole number ratio. 3. Convert % composition (mass percent) empirical formula Rhyme to remember order of steps to convert % composition empirical formula: Percent to mass Mass to mole Divide by small Times till whole Practice 1) One of the components of fresh alkaline batteries is a black powdery compound, of 63% manganese and 37% oxygen. What is the compound’s empirical formula? Practice 2) While analyzing a dead alkaline battery, Antonio finds a compound of 70.0% manganese and 30.0% oxygen. What is its empirical formula? Empirical vs. Molecular Formula Compound Empirical formula Empirical Molecular molar mass molar mass Molecular formula Formaldehyde CH2O 30.03 g 30.03 g CH2O Acetic acid CH2O 30.03 g 60.06 g C2H4O2 Glucose CH2O 30.03 g 180.18 g C6H12O6 To find the molecular formula of glucose, divide the molecular molar mass by the empirical molar mass, round to the nearest whole number. (molecular) molar mass = 180.18 g = ~ 6 empirical molar mass 30.03 g then multiply subscripts by 6 => C6H12O6 to get the molecular formula Practice Problems – Determining molecular formula Hydrazine is 87.42% N and 12.58% H. The (molecular) molar mass of hydrazine is 32.0 g/mol. a) What is its empirical formula? b) What is its molecular formula? (Hint: find the molar mass of the empirical formula) Practice Problems – Determining molecular formula Hydrazine is 87.42% N and 12.58% H. The (molecular) molar mass of hydrazine is 32.0 g/mol. a) What is its empirical formula? (NH2) b) What is its molecular formula? (N2H4) (Hint: find the molar mass of the empirical formula) Describing solution concentration – Percent by Mass Mass % of component = mass of component in solution x 100% total mass of solution Describing solution concentration – Percent by Mass e.g. In order to maintain a sodium chloride (NaCl) concentration similar to ocean water, an aquarium must contain 3.6 g NaCl per 100.0 g of water. What is the percent by mass of NaCl in the solution? Describing solution concentration – Percent by Mass 3.6 g NaCl x 100% = 3.6 g NaCl x 100% 100.0 g H2O + 3.6 g NaCl = 3.5% 103.6 g total Describing solution concentration – Percent by Mass e.g. A solution contains 2.7 g of CuSO4 in 75 mL of solution. Assume the density of the solution is 1.0 g/mL. What is the mass percent of the solution? 2.7 g (1 mL) x 100% = 3.6% 75 mL 1.0 g Molarity (Moles WS #6) • One way to measure concentration = the # moles solute dissolved in 1 L of solution Molarity ( M ) = moles of solute 1 liter of solution Molarity • Divide # moles by # liters. • If the problem gives you grams, first convert to moles by dividing by molar mass. • Also, don't forget to convert mL to L. Example A saline solution contains 0.90 g of NaCl in 100.0 mL. What is the molarity? (Molar mass of NaCl is 58.5 g.) • Begin by converting the solute and solution into the correct units. Example Begin by converting the solute and solution into the correct units. Solute: 0.90 g (1 mol NaCl) = 0.015 mol NaCl 58.5 g NaCl Solution: 100.0 mL (1 L) = 0.1000 L 103 mL Example Next, divide the number of moles by the volume of the solution: • Molarity = 0.015 mol NaCl = 0.15 M NaCl 0.1000 L Example OR, in one step: 0.90 g (1 mol NaCl) (103 mL) = 0.015 M NaCl 100.0 mL 58.5 g NaCl 1L Molarity • You can also use the molarity equation to calculate moles (and grams) or volumes (measured in L or mL). If M = mol L then M x L = # moles and L = mol M Molarity • Notice that all three of the equations above are just different algebraic versions of each other. • Use them to solve the next few problems, or use standard conversion techniques: Example of # moles = M x L How many moles of CaCl2 are in 250. mL of 2.0 M CaCl2? How many grams is this? Begin with the value you are given in the problem (250. mL), then use molarity of CaCl2 (2.0 M) as a conversion factor. Example of # moles = M x L 250. mL (1 L) (2.0 mol CaCl2) 103 mL 1L molarity as conversion factor = 0.50 mol CaCl2 then 0.50 mol CaCl2 (110.08 g CaCl2) = 55.0 g CaCl2 1 mol CaCl2 Example of # moles = M x L OR, all in one step: 250. mL (1 L) (2.0 mol CaCl2) (110.08 g CaCl2) 103 mL 1L 1 mol CaCl2 molarity as conversion factor = 55.0 g CaCl2 Example of : # L (or mL) = mol M • How many mL contain 6.25 g of 2.00 M CaCl2? • Begin with the value you are given in the problem (6.25 g), then use molarity of CaCl2 (2.00 M) as a conversion factor. Example of # L (or mL) = mol M 6.25 g CaCl2 (1 mol CaCl2) = 0.0568 mol CaCl2 110.08 g CaCl2 then 0.0568 mol CaCl2 (1 L ) (103 mL) = 28.4 mL 2.00 mol 1L Note upside down molarity Making Dilutions (Honors only) • Chemists often use concentrated (or “stock”) solutions to make dilute solutions. **The number of moles of solute does not change when a solution is diluted.** Number of moles before dilution = Number of moles after dilution Making Dilutions • Since moles = Molarity (M) x liters ( V ), then: Mc x Vc = Md x Vd e.g. How would you prepare 100. mL of 0.40 M MgSO4 from a solution of 2.0 M MgSO4 ? Mc=2.0 M Vc= ???? Md = 0.40 M Vd = 100. mL Making Dilutions Rearrange the equation: Vc = Md x Vd Mc Vc = 0.40 M x 100. mL 2.0 M = 20. mL of the concentrated solution Making Dilutions So, you would measure out 20. mL of the original solution, then add enough water to it to bring the volume to 100. mL. Important: You can do these dilution problems in either mL or L, but the V1 and V2 must both be in the same units (either both mL or both L; don't mix them up).