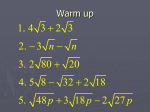Download Review: Simplifying Radicals and Complex Numbers

Review: Simplifying Radicals and Complex Numbers
Radical Review
Multiplying: You can multiply any two radicals together (if they have the same index). To multiply
radicals together: multiply inside numbers together, then multiple outside numbers together.
Ex:
1) 3 5 4 7
2)
12 35
2 3 11
3 22
*After multiply- check the number inside radical if it can be simplified*
Adding/subtracting: You can only add radicals if they have the same number on the “inside.” They must
be like terms. Just like with variables; 3x + 4x = 7x
1) 3 3
4 3
7 3
2)
3
5 this is simplified, they cannot be combined
Rationalizing the Denominator: In math a problem is not considered simplified if there is a radical in the
denominator. To “rationalize” the denominator, we multiply the numerator and denominator by the
radical in the bottom.
2
2
4
2
3
3
9
3
y
y
y
If you multiply a square root by itself, it get s to come out of the square root
Ex.
3
2
3
2
2
2
to simplify; multiply top and bottom by
3 2
2
2
Simplifying Radicals: To simplify radicals we use a factor tree and break down the radical. We then look
for pairs to “break out” of radicals (since from above we know that
Ex.
y
y
y.
80
16
4
2
5
4
2
5
2
2
5
*Hint* Best to bring down ALL factors to a
horizontal line Won’t “Miss Factors”
Look for “Doubles”
2 2
5
2
2
2 , therefore 2 comes out (twice, 2 pairs)
4 5
Simplify using multiplication of radicals
Complex Numbers: a + bi , where i is an imaginary numbers.
1
i
Taking the square root of a negative number is an error. Therefore, we call these solutions/expressions
imaginary numbers and use the i.
Ex.
4i 5
80
Same steps as above, but we just make the “negative” the i.
Homework: Radicals and Complex Numbers
Simplify all expressions, reduce down all radicals if necessary. Do not put these in the calculator, NO
decimals.
1. 5 2 4 7
4.
6 2
5
2.
2 6 4 3
5.
120
3. 13 3
6.
72
5 3