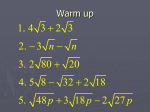Download LESSON 43 Simplifying Radical Expressions You

LESSON 43 Simplifying Radical Expressions
You have already learned the relationship between powers and roots.
The following properties of radicals work if x  0 and y  0 . They work in either order.
1.
n
xx
3.
n
x

y
1
n
n
n
2.
n
xy  n x  n y
4.
n
xm  x n 
m
x
y
 x
n
m
Note: Always take roots before powers to keep numbers smaller. For even roots, the number under the
radical must be positive to stay within the real numbers, and the root value is positive. For odd roots, the
number under the radical can be either positive or negative, and the root value has the same sign.
A few review examples from first semester.
Example 1. Change from fractional exponent form to radical form and then simplify. x  0 and y  0 .
a. 8
2
3
8
b. (27)
2
3
( 27)
 8
3
2
2
3
1
3
c. 4
1
3
4
d. 32
3
4
23

8
32
1
5

3
5
32

3
8 4
x y 
x y 
4
e.
32
1
4
4
 53
 53
3
2
 
27
3
2
3
2
4
3
8 4
x4 y8

3
 xy 
2 3
3
x3 y 6
1
23
1
8
Example 2. Simplify. (Don’t leave answers with zero or negative exponents.) Assume all variables to be
positive.
a.
64
3
b.
64  82
3
c.
64  3 43
8
e.
64
3
 16  42

2
3
5
5

64  3 (4)3
3
5
Not possible
h.
3
75 x  3  5 x  x
3
2
5 x 3x
64
d.
75x3
g.
9
9

25
25
8  2  82
4
9
25
f.
64
4
4
8 2
3
2
3
24a 6
24a 6  3 3  8  a 3a 3
 3 3  23 a 3a 3  2aa 3 3
2a 2 3 3
3
27x 6
3
i.
27 x

3
6
(3)3
3 6
x
(3)3
x3 x3

12 x8
3x3
j.
3
xx

9x 4 y 8
k.
l.
9 x4 y8
12 x8
3  4x2 x2 x2 x2

3x3
3x 2 x
 3 x x y y y y
3  22 x 2 x 2 x 2 x 2
 3 xxyyyy  3 x 2 y 4
3
x2

3x 2 x
2 x4 3
2 xxxx 3
x 3x
2
2
2
2
9x 4  y8
Not possible
2
2
2
2x 4
x x

x 3 x
When adding or subtracting radicals, the root indices must be the same, and the radicands (the numbers
underneath the radical symbols) must also be the same. Sometimes, it is necessary to simplify radicals
before they can be combined.
Example 3. Simplify.
a.
2 18  27  3 12  2
x 3 16 x  3 54 x 4
b.
2 18  27  3 12  2
x 3 16 x  3 54 x 4
2 2  32  3  32  3 3  2 2  2
x 3 2  8 x  3 2  27 xx 3
2 3 2  3 3  3 2 3  2
x 3 2  23 x  3 2  33 xx 3
6 2 3 3 6 3  2
2 x 3 2 x  3x 3 2 x
6 2  2 3 3 6 3
x 3 2x
5 2 3 3
Occasionally, it is necessary to remove radicals from denominators of fractions. This process is called
rationalizing. To rationalize a denominator containing a square root factor, simply multiply the numerator
and denominator of the fraction by that factor. If the denominator contains a higher powered root index, you
must actually think about what you should multiply by. If the denominator contains a binomial containing
one or more radicals, you should multiply by the conjugate of the denominator.
The conjugate of 5  3 2 is 5  3 2 .
Example 4. Rationalize the denominators.
a.
5
2 3
5 3
5 3 5 3


2 3 3 2 32 2  3
5 3
6
2
5
b.
2 3 52
3
3
5 5
2

2
5 3 2
c.
3
2 3 25
2 3 25
5
3
3
5
2


5 3 2
5 3 2


5 3 2

2 5 6 2
  5   3 2 
2
2
2 5 6 2 2 5 6 2 2 5 6 2


592
5  18
13
ASSIGNMENT 43: Worksheet on Simplifying Radical Expressions Problems 1-28 (see next page)