Download Everything is not normal,Some comparisons are not odious,The big

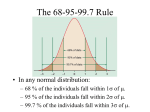
Everything is not normal
According to the dictionary, one thing is considered normal when it’s in
its natural state or conforms to standards set in advance. And this is its
normal meaning. But, like many other words, “normal” has many other
meanings. In statistics, we talking about normal we refer to a given
probability distribution that is called the normal distribution, the famous
Gauss’ bell.
This distribution is characterized by its symmetry around its mean that
coincides with its median, in addition to other features which we discussed
in a previous post. The great advantage of the normal distribution is that
it allows us to calculate probabilities of occurrence of data from this
distribution, which results in the possibility of inferring population data
using a sample obtained from it.
Thus, virtually all parametric techniques of hypothesis testing need
that data follow a normal distribution. One might think that this is not a
big problem. If it’s called normal it’ll be because biological data do
usually follow, more or less, this distribution. Big mistake, many data
follow a distribution that deviates from normal. Consider, for example, the
consumption of alcohol. The data will not be grouped symmetrically around a
mean. In contrast, the distribution will have a positive bias (to the
right): there will be a large number around zero (abstainers or very
occasional drinkers) and a long right tail formed by people with higher
consumption. The tail is long extended to the right with the consumption
values of those people who eat breakfast with bourbon.
And how affect our statistical calculations the fact that the variable
doesn’t follow a normal?. What should we do if data are not normal?.
The first thing to do is realize
that the variable is not normally
distributed. We have already seen there
are a number of graphical methods that
allow us to visually approximate if the
data follow the normal. Histograms and box-plots allow us to test whether
the distribution is skewed, if too flat or peaked, or have extreme values.
But the most specific graphic for this purpose is the normal probability
plot (q-q plot), where the values are set to the diagonal line if they are
normally distributed.
Another possibility is to use numeric contrast tests such as the
Shapiro-Wilk’s or the Kolmogorov-Smirnov’s. The problem with these tests is
that they are very sensitive to the effect of sample size. If the sample is
large they can be affected by minor deviations from normality. Conversely,
if the sample is small, they may fail to detect large deviations from
normality. But these tests also have another drawback you will understand
better after a small clarification.
We know that in any hypothesis testing we set a null hypothesis that
usually says the opposite of what we want to show. Thus, if the value of
statistical significance is lower than a set value (usually 0.05), we
reject the null hypothesis and stayed with the alternative, that says what
we want to prove. The problem is that the null hypothesis is only
falsifiable, it can never be said to be true. Simply, if the statistical
significance is high, we cannot say it’s untrue, but that does not mean
it’s true. It may happen that the study did not have enough power to reject
a null hypothesis that is, in fact, false.
Well, it happens that contrasts for normality are set with a null
hypothesis that the data follow a normal. Therefore, if the significance is
small, we can reject the null and say that the data are not normal. But if
the significance is high, we simply cannot reject it and we will say that
we have no ability to say that the data are not normal, which is not the
same as to say that the fit a normal distribution. For these reasons, it is
always advisable to complement numerical contrasts with some graphical
method to test the normality of the variable.
Once we know that the data are not normal, we
account when describing them. If the distribution
cannot use the mean as a measure of central tendency
other robust estimators such as the median or other
for these situations.
must take this into
is highly skewed we
and we must resort to
parameters available
Furthermore, the absence of normality may discourage the use of
parametric contrast tests. Student’s t test and the analysis of variance
(ANOVA) require that the distribution is normal. Student’s t is quite
robust in this regard, so that if the sample is large (n> 80) it can be
used with some confidence. But if the sample is small or very different
from the normal, we cannot use parametric contrast tests.
One of the possible solutions to this problem would be to attempt a data
transformation. The most frequently used in biology is the logarithmic
transformation, useful to approximate to a normal distribution when the
distribution is right-skewed. We mustn’t forget to undo the transformation
once the contrast in question has been made.
The other possibility is to use nonparametric tests, which require no
assumption about the distribution of the variable. Thus, to compare two
means of unpaired data we will use the Wilcoxon’s rank sum test (also
called Mann-Whitney’s U test). If data are paired we will have to use the
Wilcoxon’s sign rank test. If we compare more than two means, the Kruskal-
Wallis’ test will be the nonparametric equivalent of the ANOVA. Finally,
remember that the nonparametric equivalent of the Pearson’s correlation
coefficient is the Spearman’s correlation coefficient.
The problem is that nonparametric tests are more demanding than their
parametric equivalent to obtain statistical significance, but they must be
used as soon as there’s any doubt about the normality of the variable we’re
contrasting.
And here we will stop for today. We could have talked about a third
possibility of facing a not-normal variable, much more exotic than those
mentioned. It is the use of resampling techniques such as bootstrapping,
which consists of building an empirical distribution of the means of many
samples drawn from our data to make inferences with the results, thus
preserving the original units of the variable and avoiding the swing of
data transformation techniques. But that’s another story…
Some
odious
comparisons
are
not
It’s often said that comparisons are odious. And the truth is that it is
not appropriate to compare people or things together, since each has its
values and there’s no need of being slighted for doing something
differently. So it’s not surprising that even the Quixote said that
comparisons are always odious.
Of course, this may be said about everyday life, because in medicine we
are always comparing things together, sometimes in a rather beneficial way.
Today we are going to talk about how to compare two data distributions
graphically and we’ll look at an application of this type of comparison
that helps us to check whether our data follow a normal distribution.
Imagine for a moment that we have a hundred serum cholesterol values
from schoolchildren. What will we get if we plot the value against
themselves linearly? Simple: the result would be a perfect straight line
cross the diagonal of the graph.
Now think about what would happen if instead of comparing with
themselves we compare them with a different distribution. If the two data
distributions are very similar, the dots on the graph will be placed very
close to the diagonal. If the distributions differ, the dots will go away
from the diagonal, the further the more different the two distributions.
Let’s look at an example.
Let’
s suppose we divide our distribution into two parts, the cholesterol of
boys and girls. According to what our imagination tells us, the boys eat
more industrial bakery than the girls, so their cholesterol level are
higher, as you can see if you compare the curve from girls (black) with
those of children (blue). Now, if we represent the values of the girls
against the values of the boys linearly, as can be seen in the figure, the
dot are far from the diagonal, being evenly over it. What is the reason of
this? The values of boys are higher than the values of girls.
You will tell me that all this is fine, but it can be a bit unnecessary.
After all, if we want to know who have the highest values all that we have
to do is look at the curves. And you will be right in your reasoning, but
this type of graph has been designed for something different, which is to
compare a distribution with its normal equivalent.
Imagine that we have our first global distribution and we want to know
if it follows a normal distribution. We only have to calculate its mean and
standard deviation and represent its quantiles against the theoretical
quantiles of a normal distribution with the same mean and standard
deviation. If our data are normally distributed, the dots will align with
the diagonal of the graph. The more they go away from it, the less likely
that our data follow a normal distribution. This type of graph is called
quantile-quantile plot or, more commonly, q-q plot.
Let’s see an example of q-q plot for its better understanding. In the
second graph you can see two curves, one blue colored representing a normal
distribution and a black one following a Student’s t distribution. On the
right side you can see the q-q plot of the Student’s distribution. Central
data fits quite well the diagonal, but extreme data do it worse, varying
the slope of the line. This indicates that there are more data under the
tails of the distribution that the data that there would be if it were a
normal distribution. Of course, this should not surprise us, since we know
that the “heavy tails” are a feature of the Student’s distribution.
Finally, in the third graph you can see a normal distribution and its qq plot, in which we can see how the dots fit quite well to the diagonal of
the graph.
As you can see, the q-q plot is a simple graphical method to determine
if the data follow a normal distribution. You may say that it would be a
bit tedious to calculate the quantiles of our distribution and those of the
equivalent normal distribution, but remember that most statistical software
can do it effortlessly. For instance, R has a function called qqnorm() that
draws a q-q plot in a blink.
And here we are going to end with the normal fitting by now. Just
remember that there’re other more accurate numerical methods to find out if
data fit a normal distribution, such as the Kolmogorov-Smirnov’s test or
the Shapiro-Wilk’s test. But that’s another story…
The big family
Moviegoers do not be mistaken. We are not going to talk about the 1962
year movie in which little Chencho get lost in the Plaza Mayor at Christmas
and it takes until summer to find him, largely thanks to the search
tenacity of his grandpa. Today we’re going to talk about another large
family related to probability density functions and I hope nobody ends up
as lost as the poor Chencho on the film.
No doubt the queen of density functions is the normal distribution, the
bell-shaped. This is a probability distribution that is characterized by
its mean and standard deviation and is at the core of all the calculus of
probability and statistical inference. But there’re other continuous
probability functions that look something or much to the normal
distribution and that are also widely used when contrasting hypothesis.
The first one we’re going to talk about is the Student’s t distribution.
For those curious of science history I’ll say that the inventor of this
statistic was actually William Sealy Gosset, but as he must have liked his
name very little, he used to sign his writings under the pseudonym of
Student. Hence the name of this statistic.
This density function is a bell-shaped one that is distributed
symmetrically around its mean. It’s very similar to the normal curve,
although with a heavier tails; this is the reason why this distribution
estimates are less accurate when the sample is small, since more data under
the tails implies always the possibility of having more results far from
the mean. There are an infinite number of student’s t distributions, all of
them characterized by their mean, variance and degrees of freedom, but when
the sample size is greater than 30 (with increasing the degrees of
freedom), t distribution can be approximate to a normal distribution, so we
can use the latter without making big mistakes.
Student’s t is used to compare the means of normally distributed
populations when their sample sizes are small or when the values of the
populations variances are unknown. And this works so because if we subtract
the mean from a sample of variables and divide the result by the standard
error, the value we get follows a Student’s t distribution.
Another member of this family of continuous distributions is that of the
chi-square, which also plays an important role in statistics. If we have a
sample of normally distributed variables and we squared them, their sum
will follow a chi-square with a number of degrees of freedom equal to the
sample size. In practice, when we have a series of values of a variable, we
can subtract the expected values under the null hypothesis from the
observed ones, square these differences, and add them up to check the
probability of coming up with that value according to the density function
of a chi-square. So, we will decide whether to reject or not our null
hypothesis.
This technique can be used with three aims: determining the goodness of
fit to a theoretical population, to test the homogeneity of two populations
and to contrast the independence of two variables.
Unlike the normal distribution, chi-square’s density function only has
positive values, so it is asymmetric with a long right tail. What happens
is that the curve becomes gradually more symmetric as degrees of freedom
increase, increasingly resembling a normal distribution.
The last distribution of which we are going to talk about is the
Snedecor’s F distribution. There’s not surprise in its name about their
invention, although it seems that a certain Fisher was also involved in the
creation of this statistic.
This distribution is more related to the chi-square than to normal
distribution, because it’s de density function of the ratio of two chisquare distributions. As is easy to understand, it only has positive values
and its shape depends on the number of degrees of freedom of the two chisquare distribution that determine it. This distribution is used for the
constrast of means in the analysis of variance (ANOVA).
In summary, we can see that there’re several very similar density
function distributions to calculate probabilities and that are useful in
various hypothesis contrast. But there’re many more, as the bivariate
normal distribution, the negative binomial distribution, the uniform
distribution, and the beta and gamma distributions, to name a few. But
that’s another story…
The most famous of bells
The dictionary says that a bell is a simple device that makes a sound.
But a bell can be much more. I think there’s even a plant with that name
and a flower with its diminutive.
But undoubtedly, the most famous of all bells is the renowned Gauss’
bell curve, the most beloved and revered by statisticians and other species
of scientific.
But, what is a bell curve?. It’s nothing more, nor less, than a
probability density function. Put another way, it is a continuous
probability distribution with a symmetrical bell-shape, hence the first
part of its name. And I say the first part because the second one is more
controversial because it is not quite clear that Gauss is the father of the
child.
It seems that the first who use this density function was somebody named
Moivre, who was studying was happened to a binomial distribution when the
sample size is large. Yet another of the many injustices of History, the
name of the function is associated with Gauss, who used it some 50 years
later to record data from his astronomical studies. Of course, for defense
of Gauss, some people say the two of them discovered the density function
independently.
To avoid controversy, we will call it from now on by its other name,
different from Gauss’ bell: normal distribution. And it seems that it was
so named because people used to think that most natural phenomena were
consistent with this distribution. Later in time, it was found that
there’re other distributions that are very common in biology, such as the
binomial and Poisson’s.
As it happens with any other density function, the utility of normal
curve is that it represents the probability distribution of occurrence of
the random variable we are measuring. For example, if we measure the
weights of a population of individuals and plot it, the graph will
represent a normal distribution. Thus, the area under the curve between two
given points on the x axis represents the probability of occurrence of
those values. The total area under the curve is equal to one, which means
that there’s a 100% chance (or a probability of one) of occurrence of any
of the possible values of the distribution.
There’re infinite different normal distributions, all of them perfectly
characterized by its mean and standard deviation. Thus, any point in the
horizontal axis can be expressed as the mean plus or minus a number of
times the standard deviation and its probability can be calculated using
the formula of the density function, which I dare not so show you here. We
can also use a computer to calculate the probability of a variable within a
normal distribution, but what we do in practice is something simpler: to
standardize.
The standard normal distribution is the one that has a mean of zero and
a standard deviation of one. The advantage of the standard normal
distribution is twofold. First, we know its distribution of probabilities
among different points on the horizontal axis. So, between the mean plus or
minus one standard deviation are 68% out of the population, between the
mean and plus or minus two deviations are 95%, and between three standard
deviations 99% out of the population, approximately.
The second advantage is that any normal distribution can be transform
into a standard one, simply subtracting the mean to the value and dividing
the result by the standard deviation of the distribution. We came up so
with the z score, which is the equivalent of the value of our variable in a
standard normal distribution with mean zero and a standard deviation of
one.
So, you can see the usefulness of it. We do not need software to
calculate the probability. We just standardize and use a simple probability
table, if we do not know the value by heart. Moreover, the thing goes
beyond.
Thanks to the magic of the central limit theorem, other distributions
can be approximated to a normal one and be standardized to calculate the
probability distribution of their variables. For example, if our variable
follows a binomial distribution we can approximated it to a normal
distribution when the sample size is large. In practice, when np and n(1-p)
are greater than five. The same applies to the Poisson’s distribution,
which can be approximated to a normal when its mean is greater than 10.
And magic is twofold because besides of being able to avoid the use of
complex tools and allow us to easily calculate probabilities and confidence
intervals, it should be noted that both binomial and Poisson’s
distributions are discrete mass functions, while normal distribution is a
continuous density function.
And that’s all for now. I only want to say that there’re other
continuous density functions different from normal distribution and that
they can also be approximated to a normal when the sample is large. But
that’s another story…