Download edc-module_ia-dc_generator

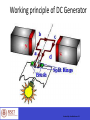
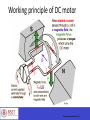
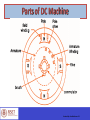
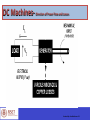
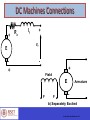
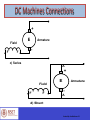
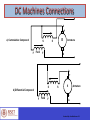
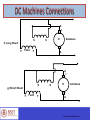
EC010504(EE) Electric
Drives & Control
Dr. Unnikrishnan P.C.
Professor, EEE
Dr. Unnikrishnan P.C.



BTech. : EEE, NSS College of Engineering,
1981-85.
MTech: Control & Instrumentation, IIT
Bombay,1990-92.
PhD. : EEE, Karpagam University,
Coimbatore, 2010-2016.
Dr. Unnikrishnan P.C.



1986-1996 : Assistant Professor and
Associate Professor, Rajasthan Technical
University, Kota, India
1996-2016 : Assistant Professor, Academic
Coordinator, Registrar, Head of Section and
Head of the Department at Colleges of
Technology, Ministry of Manpower, Muscat,
Sultanate of Oman.
2016 : Professor, EEE, RSET
Module I
 DC Generator
 DC Motor
DC Machines
Working principle of DC Generator
Working principle of DC motor
Construction of DC Machines
Parts of DC Machine
Field winding
Rotor and rotor winding
DC Machines- Direction of Power Flow and Losses
DC Machines- Direction of Power Flow and Losses
DC Machines Analysis
Symbols that will be used.
 = flux per pole
p = no. of poles
z = total number of active conductors on the armature
a = no. of parallel paths in the armature winding
Aside: Lap Winding -> a = p
Wave Winding -> a = 2
n = speed of rotation of the armature in rpm
wm = speed in radians per second
DC Machines Connections
+
Ra
If
+
VT
E
-
+
a)
Field
E
F
F
Armature
-
b) Separately Excited
DC Machines Connections
+
E
Armature
Field
F
F
-
c) Series
A
+
E
Armature
Field
F
F
d) Shunt
A
DC Machines Connections
A
+
e) Cummulative Compound
S
F
Field
E
S
Armature
F
A
A
+
S
S
E
Armature
d) Differential Compound
F
Field
F
A
DC Machines Connections
A
+
S
E
S
Armature
f) Long Shunt
F
Field
F
A
A
+
S
S
E
Armature
g) Short Shunt
F
Field
F
A
EMF Equation
When the rotor rotates in the field a voltage is developed in the
armature.
- the flux cut by one conductor in one rotation = p
- therefore in n rotations, the flux cut by one conductor = np
EMF Equation
∅𝑧𝑛 𝑝
𝑧 𝑝 𝑛 2𝜋
𝐸𝑎 =
= ∅
60 𝑎
𝑎 2𝜋 60
= ∅ 𝐾𝑎 𝜔𝑚 =𝐾𝑎 ∅ 𝜔𝑚
where 𝑘𝑎
=
𝑧𝑝
2𝜋𝑎
EMF induced in the
armature windings
TORQUE EQUATION
𝐸𝑎 𝐼𝑎 = 𝑇𝑒 𝜔𝑚
𝐸𝑎 𝐼𝑎
𝑇𝑒 =
𝜔𝑚
𝑘∅𝜔𝑚 𝐼𝑎
=
𝜔𝑚
= 𝑘∅𝐼𝑎
- In the DC machine losses are
expressed as rotational losses
due to friction and windage
(F&W).
- The torque equation can then be
rewritten as:-
SHAFT OUTPUT TORQUE = (Te -
TF&W)
DC Generator
Ia
Ea  Nz p
60 a
V  Ea  Ia R a
L
V
I  L
f R
f
Ia  I  I
f L
+
E
Rf
-
+
If
Ra
L
O
A
D
VT
-
Note: VT = VL
i.e. Terminal Voltage is the Load Voltage
OPEN CIRCUIT CHARACTERISTICS
The Open Circuit characteristic is a graph relating Open-Circuit Armature voltage of a
D.C. Generator versus its field current when the machine is driven at it’s rated speed
DC
Source
Field Regulator
Ra
ZZ
FL
Rf
F
L
OPEN
CIRCUIT
AA
Ea
V
Z
A
A
Field Current
Diagram showing motor connections for the open circuit test, separately excited
The D.C. Generator field is excited by a separate D.C. source and the current is varied using
a generator Field Regulator (a potential divider).
OPEN CIRCUIT CHARACTERISTICS
Rext is set to its maximum value. The D.C. Generator is driven at rated its speed. Rext is
decrease to a lower value so that the machine self-excites ( i.e.. Develop an e.m.f).
A
Field Current
Ra
Rext
970 ohms
Z
Rf
ZZ
A
V
VT
Ea
AA
Diagram showing the D.C. Generator as a self-excited shunt machine
EXTERNAL CHARACTERISTIC OF SHUNT GENERATOR
This is a graph relating terminal voltage and the load current of a D.C. Generator when
driven at its rated speed with the field current maintained at its normal no-load value.
A
A
Field Current
Load Current
Ra
Rext
970 ohms
Z
Rf
ZZ
A
V
Ea
Terminal
Voltage
AA
Diagram showing connections for load test.
L
O
A
D
Armature Reaction
Interaction of Main field flux with Armature field flux
Effects of Armature Reaction
It decreases the efficiency of the machine
It produces sparking at the brushes
It produces a demagnetising effect on the
main poles
It reduces the emf induced
Self excited generators some times fail to
build up emf
Armature reaction remedies
1. Brushes must be shifted to the new position of the
MNA
2. Extra turns in the field winding
3. Slots are made on the tips to increase the
reluctance
4. The laminated cores of the shoe are staggered
5. In big machines the compensating winding at pole
shoes produces a flux which just opposes the
armature mmf flux automatically.
Commutation
The change in direction of current takes place
when the conductors are along the brush axis
During this reverse process brushes short circuit
that coil and undergone commutation
Due to this sparking is produced and the
brushes will be damaged and also causes
voltage dropping.
Losses in DC Generators
1. Copper losses or variable losses
2. Stray losses or constant losses
Stray losses : consist of (a) iron losses or core losses
and (b) windage and friction losses .
Iron losses : occurs in the core of the machine due
to change of magnetic flux in the core . Consist
of hysteresis loss and eddy current loss.
Hysteresis loss depends upon the frequency ,
Flux density , volume and type of the core .
Losses
Hysteresis loss depends upon the frequency ,
Flux density , volume and type of the core .
Eddy current losses : directly proportional to
the flux density , frequency , thickness of the
lamination .
Windage and friction losses are constant due to
the opposition of wind and friction .
Applications
Shunt Generators:
a. in electro plating
b. for battery recharging
c. as exciters for AC generators.
Series Generators :
a. As boosters
b. As lighting arc lamps
DC Generator Characteristics
In general, three characteristics specify the steady-state
performance of a DC generators:
1. Open-circuit characteristics: generated voltage versus field
current at constant speed.
2. External characteristic: terminal voltage versus load current
at constant speed.
3. Load characteristic: terminal voltage versus field current at
constant armature current and speed.
DC Generator Characteristics
The terminal voltage of a dc
generator is given by
Vt  Ea  I a Ra
 f I f , m  Armature reaction drop



 I a Ra
Open-circuit and load characteristics
DC Generator Characteristics
It can be seen from the external
characteristics that the terminal
voltage falls slightly as the load
current increases. Voltage regulation
is defined as the percentage change
E V
Voltage regulation 
 100
in terminal voltage when full load is
V
removed, so that from the external
characteristics,
a
t
t
Ea  Vt
Voltage regulation 
 100
Vt
External characteristics
Self-Excited DC Shunt Generator
Maximum permissible value of the field
resistance if the terminal voltage has to build up.
Schematic diagram of connection
Open-circuit characteristic
Shunt motor:
Speed Control in DC Motors
Electromagnetic torque is Te=Ka d Ia, and the conductor emf is Ea=Vt - RaIa.
 Te 
 Ra
K a d m  Vt  
 K a d 
Vt
Te Ra
m 

K a d  K a d 2
1
For armature voltage control: Ra and If are constant
2
m  K1Vt  K 2Te
For field control: Ra and Vt are constant
m 
Vt
Ra

KfIf
KfIf


T
2 e
3
For armature resistance control: Vt and If are constant
Ra  Radj
Vt
m 

Te
K a d  K a d 2
4 
Speed Control in Shunt DC Motors
Armature Voltage Control:
Ra and If are kept constant and the armature
terminal voltage is varied to change the motor
speed.
m  K1Vt  K 2Te
K1 
1
1
; K2 
; d is const .
2
K a d
 K a d 
For constant load torque, such as applied by an
elevator or hoist crane load, the speed will
change linearly with Vt. In an actual
application, when the speed is changed by
varying the terminal voltage, the armature
current is kept constant. This method can also
be applied to series motor.
Field Control:
Speed Control in Shunt DC Motors
Ra and Vt are kept constant, field rheostat is varied to
change the field current.
m 
Vt
Ra

KfIf
KfIf

2
Te
For no-load condition, Te=0. So, no-load speed varies
inversely with the field current.
P  Vt I a  const  Ea I a  Te m
Speed control from zero to base speed
E Iis usually
const .
Te  a a 
obtained by armature voltage control.m
Speed control
m
beyond the base speed is obtained by decreasing the field
current. If armature current is not to exceed its rated
value (heating limit), speed control beyond the base
speed is restricted to constant power, known as constant
power application.
Speed Control in Shunt DC Motors
Armature Resistance Control:
Vt and If are kept constant at their rated value,
armature resistance is varied.
m 
Ra  Radj
Vt

Te  K 5  K 6Te
2
K a d  K a d 
The value of Radj can be adjusted to obtain
various speed such that the armature current Ia
(hence torque, Te=KadIa) remains constant.
Armature resistance control is simple to
implement. However, this method is less
efficient because of loss in Radj. This resistance
should also been designed to carry armature
current. It is therefore more expensive than the
rheostat used in the field control method.
Speed Control in Series DC Motors
Armature Voltage Control:
A variable dc voltage can be applied to a series motor to
control its speed. A variable dc voltage can be obtained
from a power electronic converter.
d  K s I a
Vt  Ea  I a  Ra  Rs 
 K a d m  I a  Ra  Rs 
 K a  K s I a m  I a  Ra  Rs 
Ia 
Vt
K a K s m  Ra  Rs
Torque in a series motor can be expressed as
Te  K a d I a  K a K s I a2

K a K sVt2
K K 
a
or , m 
s m
  Ra  Rs 2

Vt
R  Rs
Vt
 a

Ka K s
Te K a K s
Te K a K s
Speed Control in Series DC Motors
Armature Voltage Control:
A variable dc voltage can be applied to a series motor to
control its speed. A variable dc voltage can be obtained
from a power electronic converter.
d  K s I a
Vt  Ea  I a  Ra  Rs 
 K a d m  I a  Ra  Rs 
 K a  K s I a m  I a  Ra  Rs 
Ia 
Vt
K a K s m  Ra  Rs
Torque in a series motor can be expressed as
Te  K a d I a  K a K s I a2

K a K sVt2
K K 
a
or , m 
s m
  Ra  Rs 2

Vt
R  Rs
Vt
 a

Ka K s
Te K a K s
Te K a K s
Speed Control in Series DC Motors
Field Control:
Control of field flux in a sries motor is achieved by
using a diverter resistance.
The developed torque can be expressed as.
 Rd  2
 I a  KI a2
Te  K a d I a  K a K s 
 Rs  Rd 
Rd
where , K  K a K s and  
Rs  Rd
 Rs Rd 


Vt  Ea  
 I a  I a Ra
R

R
 s
d 
 K a d m  I a Rs  I a Ra
 K a  K sI a m  Rs  Ra I a
  Km  Rs  Ra I a
or , I a 
Vt
Km  Rs  Ra
Speed Control in Series DC Motors


Vt

Te  K
 Km  Rs  Ra 
2
Speed
Control
Armature Resistance
Control:
in Series DC Motors
Torque in this case can be expressed as
Te 
KVt2
Ra  Radj  Rs  Km 2
Rae is an external resistance connected in series with
KVt2
2
the armature.
Ra  Radj  Rs  Km 
Te
For a given supply voltage and a constant developed
torque, the term (Ra+Rae+Rs+Km) should remain
K
or
,
R

R

R

K


Vt
constant. Therefore, an increase in aRae must
adj be s
m
Te
accompanied by a corresponding decrease in m.
Ra  Radj  Rs
Vt
or , m 

K
KTe


Power Division in DC Machines
Arm. copper loss
Ia2Ra+brush contact loss
DC Generator
Input from
Elec-magnetic
Arm. terminal
Output power
prime-mover
Power =EaIa
power = Vta Ia
= V t IL
No-load rotational loss (friction
+windage+core)+stray load loss
Series field loss IL2Rs
+shunt field loss If2Rf
Arm. copper loss
Ia2Ra+brush contact loss
DC Motor
Input power from
Arm. terminal
Elec-magnetic
Output available
mains =Vt IL
power = Vta Ia
Power =EaIa
at the shaft
Series field loss IL2Rs
+shunt field loss If2Rf
No-load rotational loss (friction
+windage+core)+stray load loss
Efficiency
Power Output
Power Input
Power Input  Losses

Power Input
Losses
 1
Power Input

The losses are made up of rotational losses (3-15%), armature
circuit copper losses (3-6%), and shunt field copper loss (1-5%).
The voltage drop between the brush and commutator is 2V and
the brush contact loss is therefore calculated as 2Ia.
DC Machines Formulas
Summary
E a  V - IaR a
´
´
´

n
z
p

Ea
60 ´ a
V - I a R a ÷÷ ´ 60 ´ a
Speed n 
z´ ´ p
Ea
a
n





 I 2 R a -- Windings(Armature)
a
 I2 R -- Windings(Field )
f
f
and Rotational Losses (Windage and Friction)
Losses