Download AP Calculus

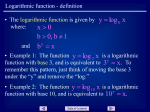
Name:
Date:
Block:
5.1 & 5.2 The Natural Logarithmic Function and Calculus
Recall that the Power Rule has an important disclaimer:
xn 1
n
x dx
C, n
1
n 1
1
We must find an antiderivative for the function f ( x)
.
x
We define this function in a new class of function called logarithmic functions. This particular function is
the natural logarithmic function.
Definition of the Natural Logarithmic Function
t
The natural logarithmic function is defined by ln x
(a) Graph of y
1
t
1
dt, x
t
1
0
(b) Graph of y
ln x
The domain of the natural logarithmic function is the set of all positive real numbers.
From the definition , we can see that ln x is ________________ for x 1 and ln x is ________________
for 0 x 1 , and ln(1) _____ when x 1.
Theorem – Properties of the Natural Logarithmic Function
The natural logarithmic function has the following properties:
, .
1. The domain is 0,
and the range is
2. The function is continuous, increasing, and one-to-one.
3. The graph is concave downward.
Logarithmic Properties
If a and b are positive numbers and n is rational, then the following properties are true:
1. ln(1) 0
2. ln ab ln a ln b
3. ln a n n ln a
a
4. ln
ln a ln b
b
If you completed your log packet then you should remember how to use these properties!!
The Number e
In logarithms you have studied so far, the logs have been defined with a base - usually base 10. For
example, log10 10 1 .
To define the base for the natural logarithm, we use the properties. There must be a real number x such
that ln x 1. This number is denoted by the letter e .
e is irrational and has the decimal approximation: e 2.71828182846
Also, log e 1 and lne 1 .
Definition of e
e
1
dt 1
t
1
You can now use logarithmic properties to evaluate the natural logarithms of several other numbers. For
example, ln e n =
The letter e denotes the positive real number such that: ln e
Using this, we can evaluate ln e n for various powers of n , as shown in the table:
x
1
e3
1
e2
e
e0
1
e
e2
ln x
Example #1 Evaluate each of the following:
a. ln 2
b. ln 32
c. ln 0.1
Theorem –Derivative of the Natural Logarithmic Function
Let u be a differentiable function of x .
d
d
1
Theorem 1
Theorem 2
[ln u]
[ln x]
, x 0
dx
x
dx
1 du
u dx
u'
, u
u
0
Example #2 Differentiate each of the following logarithmic functions:
d
d
a.
b.
ln(2 x)
ln( x 2 1)
dx
dx
c.
d
x ln x
dx
d.
d
ln x
dx
3
Napier used logarithmic properties to simplify calculations. With calculators this is no longer necessary,
but we still use the properties for differentiation.
Example #3 Differentiate f ( x)
Example #4 Differentiate f ( x)
ln x 1
ln
x x2 1
2
2x3 1
On occasion it is convenient to use logarithms as aids in differentiating non-logarithmic functions. This
procedure is called logarithmic differentiation.
Example #5 Find the derivative of y
( x 2) 2
x2
, x
2
2
Because the natural logarithm is undefined for negative numbers, you will often encounter expressions of the
form ln u . When you differentiate functions in the form y ln u do so as if the absolute value were not
present.
Theorem – Derivative Involving Absolute Value
If u is a differentiable function of x such that u
Example #6 Find the derivative of f ( x)
0 , then
d
ln u
dx
u'
u
ln cos x
Example #7 Locate the relative extrema of y
ln( x 2
2 x 3) . Justify your response.
Integration!
Theorem: Log Rule for Integration
Let u be a differentiable function of x .
1
1.
dx ln x C
x
2.
1
du ln u
u
'
Since du u dx , the second formula can also be written as
Example #1 Evaluate:
2
dx
x
C
u'
dx ln u
u
Example #2 Evaluate:
Example #3 Find the area of the region bounded by the graph of y
x
x
2
1
C
1
dx
4x 1
, the x axis, and the line x 3 .
Recognizing Quotient Forms of the Log Rule
Example #4 Evaluate each of the following:
3x 2 1
a.
dx
x3 x
c.
x 1
x 2x
2
b.
sec2 x
dx
tan x
d.
1
dx
3x 2
Note: With antiderivatives involving logarithms, it is easy to obtain forms that look quite different but are
still equivalent. Which of the following are equivalent to the antiderivative in Ex. 4d?
1
1
1
2
3
ln x
C
ln (3x 2) C
ln (3x 2) 3 C
3
3
Integrals to which the Log Rule can be applied often appear in disguised form. For instance, if a rational
function has a numerator of degree greater than or equal to that of the denominator, division may reveal a
form to which you can apply the Log Rule.
Example #5 Evaluate
x2 x 1
dx (Hint: Use long division!)
x2 1
Example #6 Evaluate
2x
dx (Hint: use change of variables)
( x 1)2
As we continue the study of integration, we will devote much time to integration techniques. To master
these techniques you must recognize the “form-fitting” nature of integration. In this sense, integration is not
nearly as straightforward as differentiation. So, be ready to THINK until the lightbulb goes off!
Guidelines for Integration:
1. Memorize a basic list of integration formulas (12 total so far: Power Rule, Log Rule, and ten trig
rules).
2. Find an integration formula that resembles all or part of the integrand, and, by trial and error, find
a choice of u that will make the integrand conform to the formula.
3. If you cannot find a u substitution that works, try altering the integrand. You might try a trig
identity, multiplication and division by the same quantity, or addition and subtraction of the same
quantity. Be creative!
Example #7 Solve the differential equation
Example #8 Evaluate
dy
dx
1
x ln x
Example #9 Evaluate sec xdx
tan xdx
Integrals for the Six Basic Trigonometric Function:
sin udu
cos u C
tan udu
ln cos u
cos udu sin u C
C
sec udu ln sec u tan u
cot udu ln sin u
C
csc udu
C
ln csc u cot u
C
4
1 tan 2 xdx
Example #10 Evaluate:
0
Example #11 The electromotive force E of a particular electrical circuit is given by E 3sin 2t where E is
measured in volts and t is measured in seconds. Find the average value of E as t ranges
from 0 to 0.5 seconds.