Download AST 346, Galaxies, Part 6

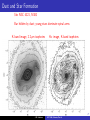
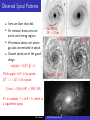
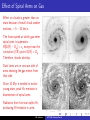
Spiral and Elliptical Galaxies
I
Spiral and S0 Galaxies
I
I
I
I
I
I
I
I
Manifested by pronounced disks, with motion dominated by rotation
rather than randomness. Little vertical motion.
S0 galaxies lack spiral features.
Both S0 and spirals can have bars in their nuclear regions.
They are composite systems: metal-poor halos, bulges and disk.
Bulge regions are very dense, gas-poor, with much random motion
(resemble small elliptical galaxies placed in a disk). They host nuclear
star clusters, with accumulated gas leading to violent star formation.
Spirals are most common galaxy and produce the bulk of light.
Massive black holes at center.
Elliptical Galaxies
I
I
I
I
I
Deceptively simple-looking
Devoid of cool gas and star formation, but have abundant hot gas,
emitting X-rays.
Wide range of luminosities and light concentrations, shapes and
rotation.
Slowly rotating systems are triaxial, rapidly rotating systems are
oblate.
Present-day ellipticals are fossils of the early Universe.
J.M. Lattimer
AST 346, Galaxies, Part 6
Surface Photometry
Isophotes in R band
Contours of CO
on R band image
Hα image
i = cos−1 (dminor /dmajor )
= cos−1 0.35 = 69◦
itrue ' 75◦
Inner isophotes are less
eccentric than outer:
Bulge is ellipsoidal, not a disk.
NGC 7331 – An Sb spiral galaxy
J.M. Lattimer
AST 346, Galaxies, Part 6
Surface Photometry
mV0 ,T = 8.75, MV0 ,T = mV0 ,T − 5 log10 (D/10 pc) = −21.9
LV ,T = 5 × 1010 L .
R∞
Ldisk = 2πIdisk (0) 0 e −R/hR RdR = 2πIdisk (0)hR2 ∼ 3 × 1010 L .
⇐ I (0) = 1.8 × 104 L pc−2
Vr = 820 km/s, D = 13.5 Mpc
disk
⇐ Idisk (0) = 325 L pc−2
3.6 kpc
⇐ sky brightness
I corrected by cos i.
NGC 7331 – An Sb spiral galaxy
J.M. Lattimer
AST 346, Galaxies, Part 6
Bulge
NGC 4594, M104, an Sa galaxy
Note large bulge and many globular clusters
Bulge dominated by older, red stars
J.M. Lattimer
AST 346, Galaxies, Part 6
Relative Luminosities and Colors
Galaxies become bluer and fainter the later the type.
Ursa Major group, D = 15 Mpc
◦ IK 0 (0) > 19.5
J.M. Lattimer
AST 346, Galaxies, Part 6
Disks Have Varying Thickness
Sd UGC 7321, i ' 87◦ ,
Ir NGC 55, i ' 80◦ ,
LB ∼ 109 L ,
LB ∼ 2 × 109 L ,
J.M. Lattimer
D = 10 Mpc
D = 1.5 Mpc
AST 346, Galaxies, Part 6
Fainter Galaxies Have More Gas
Ursa Major group
The low-surface brightness galaxies are not efficient in turning
gas into stars, like dwarf irregular galaxies.
◦ IK 0 (0) > 19.5
J.M. Lattimer
AST 346, Galaxies, Part 6
Dust and Star Formation
Sbc NGC 4321, M100
Bar hidden by dust; young stars dominate spiral arms
K-band image, 2.2µm isophotes
J.M. Lattimer
Hα image, K-band isophotes
AST 346, Galaxies, Part 6
The Bulge and Star Formation
SBb NGC 3351, M95
The bar lacks young hot stars which are concentrated in knots
in the spiral arms.
Care must be taken in interpreting images of high-redshift galaxies.
UV image, 1530Å + 2300Å
J.M. Lattimer
visible image, K-band isophotes
AST 346, Galaxies, Part 6
Dust Preferentially Absorbs UV Light
Dust absorbs UV light and re-emits it in the infrared.
T ∼ 20 − 30 K
J.M. Lattimer
AST 346, Galaxies, Part 6
Observing Cool Gas and Increasing Resolution
Signal voltages at two telescopes a
distance d apart:
V1 ∝ cos (2πνt) ,
V2 ∝ cos (2πν(t − (d/c) cos θ))
Multiply these signals in a correlator,
and filter out rapid oscillations. What
remains is a fringe pattern
d sin θ. A complete image results if
the area of a circle of radius d is
covered with dishes. If a source is
time-independent, we can put just a
few telescopes along a line and use the
Earth’s rotation to give us many
baselines.
S ∝ cos (2πν(d/c) cos θ) .
θ varies slowly as the Earth turns.
Two nearby sources produce different
fringe patterns, and as an
interferometer the telescopes can
resolve the angle c/(2dν) = λ/(2d).
The resolution is the same as a single
instrument with diameter d sin θ.
With 2 elements, a source’s position
can’t be measured, so we add
additional pairs with different baselines
J.M. Lattimer
Aperture synthesis
AST 346, Galaxies, Part 6
Cool Gas in NGC 7331
R
MHI = 2.4 × 105 M D 2
Fν [1421 MHz(1 − Vr /c)]dVr
3nH /44
photons/cm3 /Myr
D = 14 Mpc
10 = 4 kpc
Fν in Janskys
Vr in km/s
⇐ ”Spider diagram”
q northern
a southern
VLA
21 cm HI gas isophotes
Vr contours
J.M. Lattimer
AST 346, Galaxies, Part 6
Distribution and Mass of Cool Gas
2
c
/p
Gas lies in disk centered on a
ring; center is relatively
gas-poor; it extends to larger
R than stars, out to 2R25 .
0
,1
s
as
.
vs
M
1M
I= 2
dH c
s. /p
v
s M
as
M 3.6
M
Average column density of HI
is same in all spirals, due to
self-shielding; higher surface
densities make H2 at high
densities.
2
/p
5
R2
Sc NGC 891
Gas in outer regions not prone
to forming stars, due to
differential rotation?
In some galaxies, gas is
bubbled out of disk, where it
falls back.
J.M. Lattimer
AST 346, Galaxies, Part 6
c
Searching for Molecular Gas
H2 is too hard to observe, so
CO emission at mm
wavelengths is used as a
proxy. But radio instruments
are not as sensitive as they
are at cm wavelenthgs, and
CO/H2 ∼ 10−4 . It’s easier to
detect atomic gas. But maps
of molecular gas have better
spatial resolution due to
shorter wavelength.
The ratio of MHI to blue luminosity is often
used as a measure of gas-richness of a galaxy;
it is independent of D. In S0 and Sa galaxies,
this ratio is 0.05 − 0.1M /LB, . In Sc, Sd
and Sm galaxies it’s 10 times larger.
CO
In NGC 7331, there is CO
emission from a small ring at
R = 2.2hR (20 ) containing
about 3 × 109 M of H2 . This
is commmon, in other spirals
CO emission peaks at center.
J.M. Lattimer
AST 346, Galaxies, Part 6
Gas Content of S0 Galaxies
The gas content of S0
galaxies is very different from
spirals; they have almost no
gas. No recent star formation.
S0 UGC 7576
A few S0 galaxies have
1010 M of HI but it
generally lies in a tilted ring
encircling the galaxy, as in
UGC 7576 (polar ring). It was
probably captured.
J.M. Lattimer
AST 346, Galaxies, Part 6
Gas Motions and Galaxy Masses
i = 30◦
Most galactic mass is ’dark’.
For a circular orbit,
V 2 /R = G M(< R)/R 2
even for a flattened system.
HI gas has flat rotation curves
beyond the stellar distribution,
suggesting a rising M(< R).
φ=0
R/aH
Spider diagram
In spirals, dominate motion is
ordered rotation. Geometry:
Vr (R, i) = Vsys + V (R) sin i cos φ
J.M. Lattimer
HI
AST 346, Galaxies, Part 6
Rotation Curve of NGC 7331 and Dark Matter
HI
CO
stellar
J.M. Lattimer
AST 346, Galaxies, Part 6
Rotation Curves of Different Galaxies
← shows Vmax and hR
exponential disk
J.M. Lattimer
AST 346, Galaxies, Part 6
Total Mass Density of Galaxies
The Schecter function describes the
number density of galaxies:
α
Φ(L) = n∗ (L/L∗ ) e −L/L∗ ,
n∗ ' 0.02h3 Mpc3
L∗ ' 9 × 109 h−2 L
α ' −0.46
For spirals:
5h <
∼ M/L <
∼ 25h
ρgal = ρL (BJ )M/L
∼ 1 − 5 × 109 h2 M Mpc−3
Total luminosity density:
Z ∞
ρL (BJ ) =
Φ(L)LdL
< 0.02ρcrit
Deuterium abundance implies an even
larger baryon density
0
= n∗ L∗ Γ(2 + α)
' 2 × 108 h L Mpc−3
Distance to galaxies:
d ' [Vsys /100 km/s]h
Thus L ∝ h−2 , M ∝ R ∝ h−1 .
M/L ∝ h
−1
Mpc
J.M. Lattimer
2
0.02 <
∼ h ρB /ρcrit <
∼ 0.025
Most baryons are hidden, probably in
hot diffuse intergalactic gas.
AST 346, Galaxies, Part 6
The Tully-Fisher Relation
A single-dish radio telescope can
measure HI as a function of velocity,
called a global profile.
Much of the gas lies where V (R) ∼
constant, so flux is concentrated in
two peaks at ±Vmax sin i.
Brighter galaxies rotate more rapidly,
implying they are more massive.
Tully-Fisher relation:
α∼4
This correlation is better in the red or
infrared: in the blue, starburst
episodes cause significant scatter.
2
Without dark matter, M ∝ hR Vmax
,
2
2
L ∝ I (0)hR , M/L ∝ Vmax /(I (0)hR ).
4
L ∝ I (0)−1 (M/L)−2 Vmax
2Vmax
α
L ∝ Vmax
,
/s)
km
5
0
/2
ax
Vm
(
10 L L=
3
0
×1
???
J.M. Lattimer
4
K 0 ' 2.2µm
AST 346, Galaxies, Part 6
The Tully-Fisher Relation and the Hubble Constant
J.M. Lattimer
AST 346, Galaxies, Part 6
Lumpiness →
J.M. Lattimer
AST 346, Galaxies, Part 6
B
Observed Spiral Patterns
I
Arms are bluer than disk
I
Hα emission shows arms are
active star-forming regions
I
HI emission shows cool atomic
gas also concentrated in spirals
I
Clearest spirals are of the grand
design
Sbc M100
2600 = 2 kpc
B-K, Hα
cos(m[φ + f (R, t)]) = 1
Pitch angle i is 5◦ in Sa spirals,
10◦ < i < 30◦ in Sc spirals:
Sbc NGC 3949
1/ tan i = |R∂φ/∂R| = |R∂f /∂R|
If i is constant, f = ln R + k, which is
a logarithmic spiral.
J.M. Lattimer
I
AST 346, Galaxies, Part 6
B-K, HI
Spiral Patterns
Spirals are leading (tips pointed forward
wrt rotation) or trailing (tips pointed
backward wrt rotation).
Observed spirals almost always trail.
Evidence that spirals are due to density
waves (traffic jams), otherwise
differential rotation would wind them
up. Stars orbit with Ω(R) = V (R)/R;
φ = φ0 + Ω(R)t;
f (R, t) = −φ
Since dΩ/dR < 0, it follows that
df /dR > 0 and dφ/dR < 0. This is a
trailing spiral.
1/ tan ψ = Rt|dΩ/dR| ≈ 25(t/Gyr),
ψ ≈ 2◦ (Gyr/t). Stars initially on a
radial line are quickly wound into a
trailing spiral.
J.M. Lattimer
AST 346, Galaxies, Part 6
Spiral Trailing or Leading?
Is the top in front or in back?
J.M. Lattimer
AST 346, Galaxies, Part 6
Prolonging Spiral Patterns
A kinematic spiral can result if stars
are not on circular paths but on
slightly eccentric ones. Consider stars
moving about a guiding center Rg with
a epicyclic oscillation with frequency κ.
Ωp ∼ 0.3Ω so the spiral pattern lasts
longer.
An m-armed spiral could be described
by ψ = mφg (0).
φg = Ω(Rg )t
R = Rg + X cos(κt + ψ)
Consider stars at Rg with ψ = 2φg (0);
they will lie on an oval with the long
axis pointing along φ = 0.
m=2
R = X cos(κt + 2[φg (t) − Ωt])
= X cos([2Ω − κ]t − 2φg (t))
The long axis is defined by
(2Ω − κ)t = 2φ or
φ = (Ω − κ/2)t = Ωp t.
J.M. Lattimer
AST 346, Galaxies, Part 6
m=1
Maintaining Spiral Patterns
Spiral-density wave theory maintains
that gravitational attraction of stars
and gas at different radii can offset the
tendency to wind up a pairal pattern,
causing the growth of a pattern with
frequency Omegap .
The general result is that the periodic
tugging of stellar motions by a spiral
arm will reinforce the pattern only if
the perturbing frequency
m(Ωp − Ω(R)) < κ(R).
To prevent m = 0 waves from growing
κσR >
Q=
1
3.36G Σ ∼
In solar neighborhood, Q ∼ 1.4.
Trailing arms favored because inner
disk exerts a torque on the outer disk
allowing angular momentum to be
transferred outward and material to
move inward. This decreases the
rotational energy of the disk.
m = 2 Lindblad resonances
Plummer potential
Lindblad resonances occur when
m(Ωp − Ω(R)) = ±κ(R), and
reinforcement occurs between these
resonances.
Disk stars must have a small random
motion to enable reinforcement; they
cannot move outside of spiral arms.
J.M. Lattimer
ILR
ILR
AST 346, Galaxies, Part 6
Effect of Spiral Arms on Gas
Effect on clouds is greater than on
stars because of small cloud random
motions, ∼ 5 − 10 km/s.
The linear speed at which gas enters
spiral arms is supersonic:
R[Ω(R) − Ωp ] > cs except near the
corotation (CR) point Ω(R) = Ωp .
Therefore, shocks develop.
Dust lanes are on concave side of
arms showing the gas enters from
that side.
SInce 10 Myr is needed to evolve
young stars, peak Hα emission is
downstream of spiral arms.
Radiation from hot stars splits H2 ,
producing HI emission in arms.
J.M. Lattimer
AST 346, Galaxies, Part 6
Barred Disks
It is not clear why some galaxies
have bars and others do not.
Bars are not density waves, but they
do promote transfer of angular
momentum.
Within the corotation point, where
Ω(R) = Ωp , a family of closed orbits
exist. It is believed the corotation
point is external to the bar.
The elongated closed orbits converge
at the ends and is compressed into
shocks (leads to dust lanes along
leading edge of bar).
In the shock, gas loses energy of
forward motion as heat and falls to
center, but infall terminated where it
meets rounder stable orbits. Gas
piles up in a central ring.
J.M. Lattimer
AST 346, Galaxies, Part 6
Warped Extended Disk in M83
J.M. Lattimer
AST 346, Galaxies, Part 6
Bulges
Bulges are the most densely populated
stellar systems, often harboring a black
hole at their centers.
Milky Way and M31 bulges are more
metal-rich than the disk and gas-poor
except at the very center.
Bulge stars share rotation, larger
random motions than disk, σ ∼ Vc .
Bulge’s extent is Re , the half-light
radius. Studies show Re ' 0.1hR ,
ranging from 100 pc to several kpc.
Origin of bulges is not clear; their high
densities could be a result of being
older than the disk. Alternatively, they
could have formed later as gas spirals
to center. Some z > 3 galaxies are
apparently building bulges, but a rare
case, NGC 7331, has some bulge stars
orbiting opposite to the bulge itself,
J.M. Lattimer
from matter falling in at late times.
Near the center, the angular velocity is
nearly constant, so there is little
differential rotation to inhibit star
formation. In many galaxies, central
starbursts are visible, but cannot be
maintained longer than 0.1 Gyr.
At Milky Way’s center, about 107 M is
packed into a nuclear star cluster only 3
pc in radius; these are often seen in
spiral and dwarf elliptical galaxies. They
are fed by the infall of new gas and
continued star formation.
The nuclear star clusters can hide black
holes. H-burning releases 0.7% of the
rest mass as energy, but material falling
into a black hole can release 10%.
These are probably the sources of active
galactic nuclei.
AST 346, Galaxies, Part 6
Nuclear Black Holes
The black hole in Milky Way’s center is quiescent, visible by gravitational
effects. The Milky Way exhibits only a mild degree of nuclear activity,
but other galaxies have a more violent center, including jets.
NGC 4258
jets
Water maser (22.2 GHz) reveals a nuclear disk 0.01500 across (0.5 pc).
9
−3
5
ρnuc >
∼ 10 M pc , 10 × that of a globular cluster.
J.M. Lattimer
AST 346, Galaxies, Part 6
Nuclear Black Holes
Stars close to a central black
hole should move faster than
those farther out, leading to
an increased velocity
dispersion.
MBH = 2 × 108 M (σc /200km/s)4.86
rBH /D
2
V 2 (r ) ≈ G M(< r )/r >
∼ σc
4
MBH
σc
rBH
≈ 45 8
pc
10 M 100km/s
Most bright ellipticals are
radio sources, emitting power
20
P>
∼ 10 W/Hz at 20 cm,
about 10 times expected from
HII regions and SNR that
power radio emission from
spirals. Could be evidence for
MBH > 106 M .
J.M. Lattimer
AST 346, Galaxies, Part 6
Photometry of Elliptical Galaxies
Three luminosity groups:
I
I
I
Luminous giant ellipticals,
L > L∗ = 2 × 1010 L , MB <
∼ −20
Midsize ellipticals,
−20 <
∼ MB <
∼ −18
9
Dwarf ellipticals, L <
∼ 3 × 10 L ,
>
MB ∼ −18
Isophotes, contours of equal surface
brightness, are usually ellipsoidal.
Hubble type En where n = 10 with
= 1 − b/a.
Hubble type depends on our
perspective.
Concentration of light towards center
is greater than in disk galaxies,
1/n
I (R) = I (Re )e −b[(R/Re )
n = 4 (deVaucoleurs law) adequately
describes luminous and midsize
ellipticals; n = 1 describes dwarf and
disk galaxies. The total luminosity
Z ∞
L=
2πRI (R)dR
0
8!e 7.67
πRe2 I (Re )
=
7.678
≈ 7.22πRe2 I (Re )
Re = 15.800 in B band
IB (Re ) = 24.4 mag arcsec−2
BT0 = 16.4
D = 16 Mpc, L ≈ 1.1 × 108 L
Night sky: I ≈ 22.5
dE VCC753
−1]
J.M. Lattimer
(n = 4)
AST 346, Galaxies, Part 6
NGC 5846
EFAR J16WG
Note twisted contours
Zw 159-89
NGC 4478
R Band
J.M. Lattimer
AST 346, Galaxies, Part 6
Giant Ellipticals
R 1/4 law
Re = 15.700 = 1.4 kpc
Re = 4.9500 = 3.8 kpc
mag arcsec−2
The patterns observed
here reflect galaxy
formation rather than
their internal workings.
J.M. Lattimer
AST 346, Galaxies, Part 6
Centers of Ellipticals at High Resolution
Viewed from a large distance along the axis z,
Z ∞
Z ∞
n(r )rdr
√
Σ(R) = 2
n(r )dz = 2
.
r 2 − R2
0
R
Assuming n(r ) = n0 (r0 /r )α ,
r α−1
r α−1 Z ∞ x 1−α dx
0
0
√
= Σ(R = r0 )
.
Σ(R) = 2n0 r0
2−1
R
R
x
1
cusp
α = 0.55
MV = −21.7
MV = −20.9
core
-
J.M. Lattimer
Care should be taken
when interpreting a
measurement of rc
because seeing results
in only a lower bound
being measured.
AST 346, Galaxies, Part 6
True vs. Observed Shapes of Elliptical Galaxies
Oblate spheroid ρ(x) = ρ(m2 )
Fraction between i and i + di is
sin
i di. A sample with fixed ratio B/A
x +y
z
m2 =
+
will
have a fraction f (q)dq =
A2
B2
q dq
sin
i
dq
Apparent aspect ratio q = b/a, true
p
.
=p
2
|dq/di|
1 − B /A2 q 2 − B 2 /A2
ratio B/A.
2
zA
dx
If B/A << 1, this distribution is
=−
tan i =
dz
x B2
uniform; observations imply
a = mA, b = OR = OQ sin i
B/A <
∼ 0.2. No ellipticals more
2 2
flattened
than q = 0.3, possibly
OQ = OP+PQ = z−x/ tan i = B m /z
unstable.
OQ sin i
B 2m
b
=
sin i
qoblate = =
a
mA
zA
r
B2
1
=
+
sin i
2
A
tan2 i
s 2
B
=
sin2 i + cos2 i
A
−1
qprolate = qoblate
2
2
2
J.M. Lattimer
AST 346, Galaxies, Part 6
Axis Ratio and Luminosity
4.5×
J.M. Lattimer
AST 346, Galaxies, Part 6
Ordered vs. Random Velocities
cD NGC 1399
σr >> Vr − Vsys
J.M. Lattimer
AST 346, Galaxies, Part 6
Faber-Jackson Relation and the Fundamental Plane
In analogy to spirals and the Tully-Fisher Relation, ellipticals follow a
4
similar behavior
σ
LV
≈
.
2 × 1010 L
200 km/s
However, difficult to measure light from faint outer parts, errors large.
The fundamental plane relation, observationally, is Re ∝ σ 1.2 I −0.8 (Re )
r 0.8 < z < 1.2
J.M. Lattimer
AST 346, Galaxies, Part 6
Rotation and Dispersion
Most galaxies rotate less
quickly than their shapes
imply.
(V /σ)iso '
Less luminous galaxies
tend to rotate less slowly.
p
/(1 − )
r MB < −19.5
Boxy galaxies tend to
rotate more slowly.
Slow rotation must be
compensated by
anisotropic velocity
dispersion σx >> σz
PEz
KEz
σ2
=
≈ 2 z 2
PEx
KEx
V /2 + σx
Triaxiality could explain
anisotropy.
J.M. Lattimer
AST 346, Galaxies, Part 6
Boxy vs. Disky Galaxies
J.M. Lattimer
AST 346, Galaxies, Part 6
Maximum Rotation Rate Without Random Motions
Assume a uniformly rotating fluid, and approximate the gravitational
potential by a point source at the origin (Roche approximation):
ρ−1 ∇p = ∇h = −∇(ΦG + Φc )
ΦG ' −G M/r , Φc = −(1/2)Ω2 r 2 sin2 φ.
This is a perfect differential and can be integrated (Bernoulli Integral):
H = h + ΦG + Φc = −G M/Rp
Rp and Re are the polar (φ = 0) and equatorial (φ = π/2) radii.
Evaluate at equator (h = 0 on the surface):
Re
Ω2 Re3
=
−1
2G M
Rp
The maximum rotation rate is when the orbital velocity at the equator is
the same as the equatorial surface velocity:
3
Ω2max = G M/Re,max
which implies Re,max = 3Rp,min /2 or
max = 1 − Rp,min /Re,max = 1/3.
The fact that many galaxies are more flattened than this implies an
additional source of support in the plane; a large velocity dispersion.
J.M. Lattimer
AST 346, Galaxies, Part 6
Orbits in a Triaxial Potential
loop
box
chaotic
surface of section
loop
chaotic
box
J.M. Lattimer
AST 346, Galaxies, Part 6
Color-Magnitude Relation
Abell 2218
Abell 2218
Virgo and Coma
J.M. Lattimer
AST 346, Galaxies, Part 6
Metallicity-Luminosity Relation
J.M. Lattimer
AST 346, Galaxies, Part 6
Ellipticals Have High Metallicities
M87
5
0
4 =
<
r
0
8
<
r
0
4 <
kpc
T ∼ 2 × 107 K
J.M. Lattimer
AST 346, Galaxies, Part 6