* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download x - University of Pittsburgh
Survey
Document related concepts
Transcript
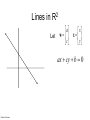
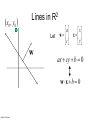
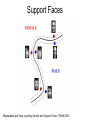
CS 1674: Intro to Computer Vision Support Vector Machines Prof. Adriana Kovashka University of Pittsburgh October 31, 2016 Plan for today • Support vector machines – Separable case / non-separable case – Linear / non-linear (kernels) • The importance of generalization – The bias-variance trade-off (applies to all classifiers) Lines in R2 Let a w c x x y ax cy b 0 Kristen Grauman Lines in R2 Let w a w c x x y ax cy b 0 wx b 0 Kristen Grauman x0 , y0 Lines in R2 Let w a w c x x y ax cy b 0 wx b 0 Kristen Grauman Lines in R2 x0 , y0 Let D w a w c x x y ax cy b 0 wx b 0 D Kristen Grauman ax0 cy0 b a c 2 2 w xb w distance from point to line Lines in R2 x0 , y0 Let D w a w c x x y ax cy b 0 wx b 0 D Kristen Grauman ax0 cy0 b a c 2 2 |w xb| w distance from point to line Linear classifiers • Find linear function to separate positive and negative examples xi positive : xi w b 0 xi negative : xi w b 0 Which line is best? C. Burges, A Tutorial on Support Vector Machines for Pattern Recognition, Data Mining and Knowledge Discovery, 1998 Support vector machines • Discriminative classifier based on optimal separating line (for 2d case) • Maximize the margin between the positive and negative training examples C. Burges, A Tutorial on Support Vector Machines for Pattern Recognition, Data Mining and Knowledge Discovery, 1998 Support vector machines • Want line that maximizes the margin. Support vectors xi positive ( yi 1) : xi w b 1 xi negative ( yi 1) : xi w b 1 For support, vectors, xi w b 1 Margin C. Burges, A Tutorial on Support Vector Machines for Pattern Recognition, Data Mining and Knowledge Discovery, 1998 Support vector machines • Want line that maximizes the margin. xi positive ( yi 1) : xi w b 1 xi negative ( yi 1) : xi w b 1 For support, vectors, xi w b 1 Distance between point and line: Support vectors Margin | xi w b | || w || For support vectors: wΤ x b 1 1 1 2 M w w w w w C. Burges, A Tutorial on Support Vector Machines for Pattern Recognition, Data Mining and Knowledge Discovery, 1998 Support vector machines • Want line that maximizes the margin. xi positive ( yi 1) : xi w b 1 xi negative ( yi 1) : xi w b 1 For support, vectors, xi w b 1 Distance between point and line: | xi w b | || w || Therefore, the margin is 2 / ||w|| Support vectors Margin C. Burges, A Tutorial on Support Vector Machines for Pattern Recognition, Data Mining and Knowledge Discovery, 1998 Finding the maximum margin line 1. Maximize margin 2/||w|| 2. Correctly classify all training data points: xi positive ( yi 1) : xi w b 1 xi negative ( yi 1) : xi w b 1 Quadratic optimization problem: 1 T Minimize w w 2 Subject to yi(w·xi+b) ≥ 1 One constraint for each training point. Note sign trick. C. Burges, A Tutorial on Support Vector Machines for Pattern Recognition, Data Mining and Knowledge Discovery, 1998 Finding the maximum margin line • Solution: w i i yi xi Learned weight Support vector C. Burges, A Tutorial on Support Vector Machines for Pattern Recognition, Data Mining and Knowledge Discovery, 1998 Finding the maximum margin line • Solution: w i i yi xi b = yi – w·xi (for any support vector) • Classification function: f ( x) sign (w x b) sign y x x b i i i i If f(x) < 0, classify as negative, otherwise classify as positive. • Notice that it relies on an inner product between the test point x and the support vectors xi • (Solving the optimization problem also involves computing the inner products xi · xj between all pairs of training points) C. Burges, A Tutorial on Support Vector Machines for Pattern Recognition, Data Mining and Knowledge Discovery, 1998 Nonlinear SVMs • Datasets that are linearly separable work out great: x 0 • But what if the dataset is just too hard? x 0 • We can map it to a higher-dimensional space: x2 0 Andrew Moore x Nonlinear SVMs • General idea: the original input space can always be mapped to some higher-dimensional feature space where the training set is separable: Φ: x → φ(x) Andrew Moore Nonlinear kernel: Example 2 • Consider the mapping ( x) ( x, x ) x2 ( x) ( y) ( x, x 2 ) ( y, y 2 ) xy x 2 y 2 K ( x, y) xy x 2 y 2 Svetlana Lazebnik The “Kernel Trick” • The linear classifier relies on dot product between vectors K(xi ,xj) = xi · xj • If every data point is mapped into high-dimensional space via some transformation Φ: xi → φ(xi ), the dot product becomes: K(xi ,xj) = φ(xi ) · φ(xj) • A kernel function is similarity function that corresponds to an inner product in some expanded feature space • The kernel trick: instead of explicitly computing the lifting transformation φ(x), define a kernel function K such that: K(xi ,xj) = φ(xi ) · φ(xj) Andrew Moore Examples of kernel functions K ( xi , x j ) xi x j T Linear: Polynomials of degree up to d: 𝐾(𝑥𝑖 , 𝑥𝑗 ) = (𝑥𝑖 𝑇 𝑥𝑗 + 1)𝑑 2 Gaussian RBF: xi x j K ( xi ,x j ) exp( ) 2 2 Histogram intersection: K ( xi , x j ) min( xi (k ), x j (k )) k Andrew Moore / Carlos Guestrin Allowing misclassifications: Before The w that minimizes… Maximize margin Allowing misclassifications: After Misclassification cost # data samples Slack variable The w that minimizes… Maximize margin Minimize misclassification What about multi-class SVMs? • Unfortunately, there is no “definitive” multi-class SVM formulation • In practice, we have to obtain a multi-class SVM by combining multiple two-class SVMs • One vs. others – Training: learn an SVM for each class vs. the others – Testing: apply each SVM to the test example, and assign it to the class of the SVM that returns the highest decision value • One vs. one – Training: learn an SVM for each pair of classes – Testing: each learned SVM “votes” for a class to assign to the test example Svetlana Lazebnik Multi-class problems • One-vs-all (a.k.a. one-vs-others) – Train K classifiers – In each, pos = data from class i, neg = data from classes other than i – The class with the most confident prediction wins – Example: • • • • • • You have 4 classes, train 4 classifiers 1 vs others: score 3.5 2 vs others: score 6.2 3 vs others: score 1.4 4 vs other: score 5.5 Final prediction: class 2 Multi-class problems • One-vs-one (a.k.a. all-vs-all) – Train K(K-1)/2 binary classifiers (all pairs of classes) – They all vote for the label – Example: • • • • You have 4 classes, then train 6 classifiers 1 vs 2, 1 vs 3, 1 vs 4, 2 vs 3, 2 vs 4, 3 vs 4 Votes: 1, 1, 4, 2, 4, 4 Final prediction is class 4 SVMs for recognition 1. Define your representation for each example. 2. Select a kernel function. 3. Compute pairwise kernel values between labeled examples 4. Use this “kernel matrix” to solve for SVM support vectors & weights. 5. To classify a new example: compute kernel values between new input and support vectors, apply weights, check sign of output. Kristen Grauman Example: learning gender with SVMs Moghaddam and Yang, Learning Gender with Support Faces, TPAMI 2002. Moghaddam and Yang, Face & Gesture 2000. Kristen Grauman Learning gender with SVMs • Training examples: – 1044 males – 713 females • Experiment with various kernels, select Gaussian RBF K (xi , x j ) exp( Kristen Grauman xi x j 2 2 2 ) Support Faces Moghaddam and Yang, Learning Gender with Support Faces, TPAMI 2002. Moghaddam and Yang, Learning Gender with Support Faces, TPAMI 2002. Gender perception experiment: How well can humans do? • Subjects: – 30 people (22 male, 8 female) – Ages mid-20’s to mid-40’s • Test data: – 254 face images (6 males, 4 females) – Low res and high res versions • Task: – Classify as male or female, forced choice – No time limit Moghaddam and Yang, Face & Gesture 2000. Gender perception experiment: How well can humans do? Error Moghaddam and Yang, Face & Gesture 2000. Error Human vs. Machine • SVMs performed better than any single human test subject, at either resolution Kristen Grauman SVMs: Pros and cons • Pros • Many publicly available SVM packages: http://www.csie.ntu.edu.tw/~cjlin/libsvm/ or use built-in Matlab version (but slower) • Kernel-based framework is very powerful, flexible • Often a sparse set of support vectors – compact at test time • Work very well in practice, even with very small training sample sizes • Cons • No “direct” multi-class SVM, must combine two-class SVMs • Can be tricky to select best kernel function for a problem • Computation, memory – During training time, must compute matrix of kernel values for every pair of examples – Learning can take a very long time for large-scale problems Adapted from Lana Lazebnik Precision / Recall / F-measure True positives (images that contain people) True negatives (images that do not contain people) Predicted positives (images predicted to contain people) Predicted negatives (images predicted not to contain people) • • • Precision Recall F-measure = 2 / 5 = 0.4 = 2 / 4 = 0.5 = 2*0.4*0.5 / 0.4+0.5 = 0.44 Accuracy: 5 / 10 = 0.5 Generalization Training set (labels known) Test set (labels unknown) • How well does a learned model generalize from the data it was trained on to a new test set? Slide credit: L. Lazebnik Generalization • Components of generalization error – Bias: how much the average model over all training sets differs from the true model • Error due to inaccurate assumptions/simplifications made by the model – Variance: how much models estimated from different training sets differ from each other • Underfitting: model is too “simple” to represent all the relevant class characteristics – High bias and low variance – High training error and high test error • Overfitting: model is too “complex” and fits irrelevant characteristics (noise) in the data – Low bias and high variance – Low training error and high test error Slide credit: L. Lazebnik Bias-Variance Trade-off • Models with too few parameters are inaccurate because of a large bias (not enough flexibility). • Models with too many parameters are inaccurate because of a large variance (too much sensitivity to the sample). Slide credit: D. Hoiem Fitting a model Is this a good fit? Figures from Bishop With more training data Figures from Bishop Bias-variance tradeoff Overfitting Error Underfitting Test error Training error High Bias Low Variance Complexity Low Bias High Variance Slide credit: D. Hoiem Bias-variance tradeoff Test Error Few training examples High Bias Low Variance Many training examples Complexity Low Bias High Variance Slide credit: D. Hoiem Choosing the trade-off • Need validation set • Validation set is separate from the test set Error Validation error Training error High Bias Low Variance Complexity Low Bias High Variance Slide credit: D. Hoiem Effect of Training Size Error Fixed prediction model Testing Generalization Error Training Number of Training Examples Adapted from D. Hoiem How to reduce variance? • Choose a simpler classifier • Use fewer features • Get more training data • Regularize the parameters Slide credit: D. Hoiem Regularization No regularization Figures from Bishop Huge regularization Characteristics of vision learning problems • Lots of continuous features – Spatial pyramid may have ~15,000 features • Imbalanced classes – Often limited positive examples, practically infinite negative examples • Difficult prediction tasks • Recently, massive training sets became available – If we have a massive training set, we want classifiers with low bias (high variance is ok) and reasonably efficient training Adapted from D. Hoiem Remember… • No free lunch: machine learning algorithms are tools • Three kinds of error – Inherent: unavoidable – Bias: due to over-simplifications – Variance: due to inability to perfectly estimate parameters from limited data • Try simple classifiers first • Better to have smart features and simple classifiers than simple features and smart classifiers • Use increasingly powerful classifiers with more training data (bias-variance tradeoff) Adapted from D. Hoiem