Download PPT

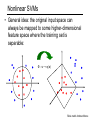
Classifiers
• Given a feature representation for images,
how do we learn a model for distinguishing
features from different classes?
Decision
boundary
Zebra
Non-zebra
Classifiers
• Given a feature representation for images,
how do we learn a model for distinguishing
features from different classes?
• Today:
•
•
Nearest neighbor classifiers
Linear classifiers: support vector machines
• Later:
•
•
•
Boosting
Decision trees and forests
Deep neural networks (hopefully)
Review: Nearest Neighbor Classifier
Review: Nearest Neighbor Classifier
• Assign label of nearest training data point to
each test data point
from Duda et al.
Review: K-Nearest Neighbors
• For a new point, find the k closest points
from training data
• Labels of the k points “vote” to classify
k=5
Distance functions for bags of features
• Euclidean distance: D(h1 , h 2 ) 
• L1 distance:
•
distance:
2
(
h
(
i
)

h
(
i
))
 1
2
i 1
N
D(h1 , h 2 )   | h1 (i )  h 2 (i ) |
i 1
χ2
N
N
h1 (i)  h 2 (i) 
i 1
h1 (i )  h 2 (i )
D(h1 , h 2 )  
2
• Histogram intersection (similarity):
N
I (h1 , h 2 )   min(h1 (i ), h 2 (i ))
i 1
• Hellinger kernel (similarity):
N
K (h1 , h 2 )   h1 (i ) h 2 (i )
i 1
Review: Linear classifiers
Review: Linear classifiers
• Find linear function (hyperplane) to separate
positive and negative examples
xi positive :
xi  w  b  0
xi negative :
xi  w  b  0
Which hyperplane
is best?
Support vector machines
• Find hyperplane that maximizes the margin
between the positive and negative examples
C. Burges, A Tutorial on Support Vector Machines for Pattern Recognition, Data Mining
and Knowledge Discovery, 1998
Support vector machines
• Find hyperplane that maximizes the margin
between the positive and negative examples
xi positive ( yi  1) :
xi  w  b  1
xi negative ( yi  1) :
xi  w  b  1
For support vectors,
xi  w  b  1
Distance between point
and hyperplane:
| xi  w  b |
|| w ||
Therefore, the margin is 2 / ||w||
Support vectors
Margin
C. Burges, A Tutorial on Support Vector Machines for Pattern Recognition, Data Mining
and Knowledge Discovery, 1998
Finding the maximum margin hyperplane
1. Maximize margin 2 / ||w||
2. Correctly classify all training data:
xi positive ( yi  1) :
xi  w  b  1
xi negative ( yi  1) :
xi  w  b  1
Quadratic optimization problem:
1
min w
w ,b 2
2
subject to
yi ( w  x i  b )  1
C. Burges, A Tutorial on Support Vector Machines for Pattern Recognition, Data Mining
and Knowledge Discovery, 1998
Finding the maximum margin hyperplane
• Solution: w  i  i yi xi
Learned weight
(nonzero only for support vectors)
C. Burges, A Tutorial on Support Vector Machines for Pattern Recognition, Data Mining
and Knowledge Discovery, 1998
Finding the maximum margin hyperplane
• Solution: w  i  i yi xi
b = yi – w·xi for any support vector
• Classification function (decision boundary):
w  x  b  i  i yi xi  x  b
• Notice that it relies on an inner product between
the test point x and the support vectors xi
• Solving the optimization problem also involves
computing the inner products xi · xj between all
pairs of training points
C. Burges, A Tutorial on Support Vector Machines for Pattern Recognition, Data Mining
and Knowledge Discovery, 1998
What if the data is not linearly separable?
1
w
• Separable: min
w ,b 2
2
subject to
yi ( w  x i  b )  1
n
1
2
• Non-separable: min w  C   i
w ,b 2
i 1
subject to yi (w  x i  b)  1   i  0
•
•
•
C: tradeoff constant, ξi : slack variable (positive)
Whenever margin is ≥ 1, ξi = 0
Whenever margin is < 1,  i  1  yi ( w  x i  b)
What if the data is not linearly separable?
1
2
min w  C
w ,b 2
Maximize
margin
n
 max0,1  y (w  x
i 1
i
i
 b) 
Minimize classification
mistakes
What if the data is not linearly separable?
1
2
min w  C
w ,b 2
n
 max 0,1  y (w  x
i 1
i
i
 b) 
+1
Margin
-1
0
Demo: http://cs.stanford.edu/people/karpathy/svmjs/demo
Nonlinear SVMs
• Datasets that are linearly separable work out great:
x
0
• But what if the dataset is just too hard?
x
0
• We can map it to a higher-dimensional space:
x2
0
x
Slide credit: Andrew Moore
Nonlinear SVMs
• General idea: the original input space can
always be mapped to some higher-dimensional
feature space where the training set is
separable:
Φ: x → φ(x)
Slide credit: Andrew Moore
Nonlinear SVMs
• The kernel trick: instead of explicitly computing
the lifting transformation φ(x), define a kernel
function K such that
K(x,y) = φ(x) · φ(y)
(to be valid, the kernel function must satisfy
Mercer’s condition)
• This gives a nonlinear decision boundary in the
original feature space:
  y  ( x )   ( x)  b    y K ( x , x)  b
i
i
i
i
i
i
i
i
C. Burges, A Tutorial on Support Vector Machines for Pattern Recognition, Data Mining
and Knowledge Discovery, 1998
Nonlinear kernel: Example
2
• Consider the mapping  ( x)  ( x, x )
x2
 ( x)   ( y)  ( x, x 2 )  ( y, y 2 )  xy  x 2 y 2
K ( x, y)  xy  x 2 y 2
Polynomial kernel: K (x, y )  (c  x  y )
d
Gaussian kernel
• Also known as the radial basis function (RBF)
kernel:
2
 1
K (x, y )  exp  2 x  y 
 

• The corresponding mapping φ(x) is infinitedimensional!
Gaussian kernel
SV’s
Gaussian kernel
• Also known as the radial basis function (RBF)
kernel:
2
 1
K (x, y )  exp  2 x  y 
 

• The corresponding mapping φ(x) is infinitedimensional!
• What is the role of parameter σ?
•
•
What if σ is close to zero?
What if σ is very large?
Kernels for bags of features
• Histogram intersection kernel:
N
I (h1 , h 2 )   min(h1 (i ), h 2 (i ))
i 1
• Hellinger kernel:
N
K (h1 , h 2 )   h1 (i ) h 2 (i )
i 1
• Generalized Gaussian kernel:
 1
2
K (h1 , h 2 )  exp  D(h1 , h 2 ) 
 A

• D can be L1, Euclidean, χ2 distance, etc.
J. Zhang, M. Marszalek, S. Lazebnik, and C. Schmid, Local Features and Kernels for
Classifcation of Texture and Object Categories: A Comprehensive Study, IJCV 2007
Summary: SVMs for image classification
1. Pick an image representation (in our case, bag
of features)
2. Pick a kernel function for that representation
3. Compute the matrix of kernel values between
every pair of training examples
4. Feed the kernel matrix into your favorite SVM
solver to obtain support vectors and weights
5. At test time: compute kernel values for your test
example and each support vector, and combine
them with the learned weights to get the value of
the decision function
What about multi-class SVMs?
• Unfortunately, there is no “definitive” multiclass SVM formulation
• In practice, we have to obtain a multi-class
SVM by combining multiple two-class SVMs
• One vs. others
• Traning: learn an SVM for each class vs. the others
• Testing: apply each SVM to test example and assign to it the
class of the SVM that returns the highest decision value
• One vs. one
• Training: learn an SVM for each pair of classes
• Testing: each learned SVM “votes” for a class to assign to
the test example
SVMs: Pros and cons
• Pros
• Many publicly available SVM packages:
http://www.kernel-machines.org/software
• Kernel-based framework is very powerful, flexible
• SVMs work very well in practice, even with very small
training sample sizes
• Cons
• No “direct” multi-class SVM, must combine two-class SVMs
• Computation, memory
– During training time, must compute matrix of kernel values for
every pair of examples
– Learning can take a very long time for large-scale problems
SVMs for large-scale datasets
• Efficient linear solvers
•
LIBLINEAR, PEGASOS
• Explicit approximate embeddings: define an
explicit mapping φ(x) such that φ(x) · φ(y)
approximates K(x,y) and train a linear SVM
on top of that embedding
•
•
Random Fourier features for the Gaussian kernel
(Rahimi and Recht, 2007)
Embeddings for additive kernels, e.g., histogram
intersection (Maji et al., 2013, Vedaldi and
Zisserman, 2012)
Summary: Classifiers
• Nearest-neighbor and k-nearest-neighbor
classifiers
• Support vector machines
•
•
•
•
•
•
Linear classifiers
Margin maximization
Non-separable case
The kernel trick
Multi-class SVMs
Large-scale SVMs
• Of course, there are many other classifiers
out there
• Neural networks, boosting, decision trees/forests, …