* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download PPT
Survey
Document related concepts
Transcript
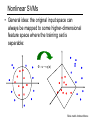
Classifiers • Given a feature representation for images, how do we learn a model for distinguishing features from different classes? Decision boundary Zebra Non-zebra Classifiers • Given a feature representation for images, how do we learn a model for distinguishing features from different classes? • Today: • • Nearest neighbor classifiers Linear classifiers: support vector machines • Later: • • • Boosting Decision trees and forests Deep neural networks (hopefully) Review: Nearest Neighbor Classifier Review: Nearest Neighbor Classifier • Assign label of nearest training data point to each test data point from Duda et al. Review: K-Nearest Neighbors • For a new point, find the k closest points from training data • Labels of the k points “vote” to classify k=5 Distance functions for bags of features • Euclidean distance: D(h1 , h 2 ) • L1 distance: • distance: 2 ( h ( i ) h ( i )) 1 2 i 1 N D(h1 , h 2 ) | h1 (i ) h 2 (i ) | i 1 χ2 N N h1 (i) h 2 (i) i 1 h1 (i ) h 2 (i ) D(h1 , h 2 ) 2 • Histogram intersection (similarity): N I (h1 , h 2 ) min(h1 (i ), h 2 (i )) i 1 • Hellinger kernel (similarity): N K (h1 , h 2 ) h1 (i ) h 2 (i ) i 1 Review: Linear classifiers Review: Linear classifiers • Find linear function (hyperplane) to separate positive and negative examples xi positive : xi w b 0 xi negative : xi w b 0 Which hyperplane is best? Support vector machines • Find hyperplane that maximizes the margin between the positive and negative examples C. Burges, A Tutorial on Support Vector Machines for Pattern Recognition, Data Mining and Knowledge Discovery, 1998 Support vector machines • Find hyperplane that maximizes the margin between the positive and negative examples xi positive ( yi 1) : xi w b 1 xi negative ( yi 1) : xi w b 1 For support vectors, xi w b 1 Distance between point and hyperplane: | xi w b | || w || Therefore, the margin is 2 / ||w|| Support vectors Margin C. Burges, A Tutorial on Support Vector Machines for Pattern Recognition, Data Mining and Knowledge Discovery, 1998 Finding the maximum margin hyperplane 1. Maximize margin 2 / ||w|| 2. Correctly classify all training data: xi positive ( yi 1) : xi w b 1 xi negative ( yi 1) : xi w b 1 Quadratic optimization problem: 1 min w w ,b 2 2 subject to yi ( w x i b ) 1 C. Burges, A Tutorial on Support Vector Machines for Pattern Recognition, Data Mining and Knowledge Discovery, 1998 Finding the maximum margin hyperplane • Solution: w i i yi xi Learned weight (nonzero only for support vectors) C. Burges, A Tutorial on Support Vector Machines for Pattern Recognition, Data Mining and Knowledge Discovery, 1998 Finding the maximum margin hyperplane • Solution: w i i yi xi b = yi – w·xi for any support vector • Classification function (decision boundary): w x b i i yi xi x b • Notice that it relies on an inner product between the test point x and the support vectors xi • Solving the optimization problem also involves computing the inner products xi · xj between all pairs of training points C. Burges, A Tutorial on Support Vector Machines for Pattern Recognition, Data Mining and Knowledge Discovery, 1998 What if the data is not linearly separable? 1 w • Separable: min w ,b 2 2 subject to yi ( w x i b ) 1 n 1 2 • Non-separable: min w C i w ,b 2 i 1 subject to yi (w x i b) 1 i 0 • • • C: tradeoff constant, ξi : slack variable (positive) Whenever margin is ≥ 1, ξi = 0 Whenever margin is < 1, i 1 yi ( w x i b) What if the data is not linearly separable? 1 2 min w C w ,b 2 Maximize margin n max0,1 y (w x i 1 i i b) Minimize classification mistakes What if the data is not linearly separable? 1 2 min w C w ,b 2 n max 0,1 y (w x i 1 i i b) +1 Margin -1 0 Demo: http://cs.stanford.edu/people/karpathy/svmjs/demo Nonlinear SVMs • Datasets that are linearly separable work out great: x 0 • But what if the dataset is just too hard? x 0 • We can map it to a higher-dimensional space: x2 0 x Slide credit: Andrew Moore Nonlinear SVMs • General idea: the original input space can always be mapped to some higher-dimensional feature space where the training set is separable: Φ: x → φ(x) Slide credit: Andrew Moore Nonlinear SVMs • The kernel trick: instead of explicitly computing the lifting transformation φ(x), define a kernel function K such that K(x,y) = φ(x) · φ(y) (to be valid, the kernel function must satisfy Mercer’s condition) • This gives a nonlinear decision boundary in the original feature space: y ( x ) ( x) b y K ( x , x) b i i i i i i i i C. Burges, A Tutorial on Support Vector Machines for Pattern Recognition, Data Mining and Knowledge Discovery, 1998 Nonlinear kernel: Example 2 • Consider the mapping ( x) ( x, x ) x2 ( x) ( y) ( x, x 2 ) ( y, y 2 ) xy x 2 y 2 K ( x, y) xy x 2 y 2 Polynomial kernel: K (x, y ) (c x y ) d Gaussian kernel • Also known as the radial basis function (RBF) kernel: 2 1 K (x, y ) exp 2 x y • The corresponding mapping φ(x) is infinitedimensional! Gaussian kernel SV’s Gaussian kernel • Also known as the radial basis function (RBF) kernel: 2 1 K (x, y ) exp 2 x y • The corresponding mapping φ(x) is infinitedimensional! • What is the role of parameter σ? • • What if σ is close to zero? What if σ is very large? Kernels for bags of features • Histogram intersection kernel: N I (h1 , h 2 ) min(h1 (i ), h 2 (i )) i 1 • Hellinger kernel: N K (h1 , h 2 ) h1 (i ) h 2 (i ) i 1 • Generalized Gaussian kernel: 1 2 K (h1 , h 2 ) exp D(h1 , h 2 ) A • D can be L1, Euclidean, χ2 distance, etc. J. Zhang, M. Marszalek, S. Lazebnik, and C. Schmid, Local Features and Kernels for Classifcation of Texture and Object Categories: A Comprehensive Study, IJCV 2007 Summary: SVMs for image classification 1. Pick an image representation (in our case, bag of features) 2. Pick a kernel function for that representation 3. Compute the matrix of kernel values between every pair of training examples 4. Feed the kernel matrix into your favorite SVM solver to obtain support vectors and weights 5. At test time: compute kernel values for your test example and each support vector, and combine them with the learned weights to get the value of the decision function What about multi-class SVMs? • Unfortunately, there is no “definitive” multiclass SVM formulation • In practice, we have to obtain a multi-class SVM by combining multiple two-class SVMs • One vs. others • Traning: learn an SVM for each class vs. the others • Testing: apply each SVM to test example and assign to it the class of the SVM that returns the highest decision value • One vs. one • Training: learn an SVM for each pair of classes • Testing: each learned SVM “votes” for a class to assign to the test example SVMs: Pros and cons • Pros • Many publicly available SVM packages: http://www.kernel-machines.org/software • Kernel-based framework is very powerful, flexible • SVMs work very well in practice, even with very small training sample sizes • Cons • No “direct” multi-class SVM, must combine two-class SVMs • Computation, memory – During training time, must compute matrix of kernel values for every pair of examples – Learning can take a very long time for large-scale problems SVMs for large-scale datasets • Efficient linear solvers • LIBLINEAR, PEGASOS • Explicit approximate embeddings: define an explicit mapping φ(x) such that φ(x) · φ(y) approximates K(x,y) and train a linear SVM on top of that embedding • • Random Fourier features for the Gaussian kernel (Rahimi and Recht, 2007) Embeddings for additive kernels, e.g., histogram intersection (Maji et al., 2013, Vedaldi and Zisserman, 2012) Summary: Classifiers • Nearest-neighbor and k-nearest-neighbor classifiers • Support vector machines • • • • • • Linear classifiers Margin maximization Non-separable case The kernel trick Multi-class SVMs Large-scale SVMs • Of course, there are many other classifiers out there • Neural networks, boosting, decision trees/forests, …