Download Lecture 11

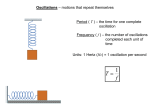
Physics 106 Lecture 11
Oscillations – I
SJ 7th Ed.: Chap 15.1 to 3, 15.5
• Oscillating systems
– Characterization
– Examples: they are everywhere
– Key concepts
• Simple harmonic motion: a paradigm
– Representation for displacement, velocity,
acceleration
– Oscillator equation
•
•
•
•
SHM example: spring oscillator (Hooke’s law)
Energy
gy relations, example
p
SHM example: torsion pendulum
SHM example: simple pendulum
Definition of an Oscillator
:
A system executing periodic, repetitive behavior
• System state (t) = state(t+T) = …= state(t+NT)
• T = period = time to complete one complete cycle
• State can mean: position / velocity, electric and magnetic fields, others…
Example: simple harmonic oscillator
G
G
Hooke' s Law restoring force : F = - kx
Emech = constant = K + Uel =
1
1
mv 2 + kx 2
2
2
Oscillation range limited by: Kmax = Umax
Spring oscillator is the pattern for many systems
Can represent it also by circular motion
e.g., x-component of a mass on a rotating stick)
1
Oscillating systems are everywhere in nature:
MECHANICAL:
• pendula (swinging objects on cables)
• auto suspensions
• music/sound (e.g,string instruments)
• guitar, piano, drums, bells, horns, reeds…
• rotating
g machines,, vehicle wheels,, orbits,, structures,,
Simple
systems
spring
y
pendulum
θ(t)
x(t)
L
v(t)
a(t)
θ
m
vibrating string
ω(t)
α(t)
y(t)
vy(t)
ay(t)
x(t)
m
θ
x
vx(t)
ax(t)
uniform circular motion
Electrical examples:
• clocks, radios driven by oscillator circuits
• atomic and molecular energy states
• light, x-rays, IR, radio, other EM waves
• antennas, transmitters
• the stable shapes of solid objects
Simple Harmonic Oscillators applied to solids
•
•
Simple harmonic oscillators are good models of a wide variety of
physical phenomena
Molecular example
– If the atoms in the molecule do not move too far, the forces between
them can be modeled as if there were springs between the atoms
– The potential energy acts similar to that of the SHM oscillator
simple
oscillator
realistic
potential
2
Water Waves:
Harmonic oscillations of the level at a point
disturbance
y1 (t ) = y10 cos( 2πft )
The phase angle
Φ sets the clock
v
y 2 (t ) = y 20 cos( 2πft + φ)
v
Some concepts for oscillations
restoring
force:
natural
frequency:
A force causes the system to return to some equilibrium
state periodically and repeat the motion
Resonant oscillation period, determined by physics of the
system alone. Disturb system to start, then let it go.
E
Examples:
l
pendulum
d l
clock,
l k violin
i li string
ti
undamped
oscillations:
Idealized case, no energy lost, motion persists forever
Example: orbit of electrons in atoms and molecules
damped
oscillations:
Oscillation dies away due to loss of energy, converted to heat
or another form. Example: a swing eventually stops
simple
harmon c
harmonic
oscillation:
Undamped natural oscillation with F = - kx (Hooke’s Law);
i e restoring force is proportional to the displacement away
i.e.
from the equilibrium state
forced
oscillations:
External periodic force drives the system motion at it’s own
frequency/period, may not be the resonant frequency
3
Characterizing oscillations
Amplitude xmax
• maximum displacement away
from equilibrium (disturbance)
displacement
Period T
• time for motion to repeat
time
Frequency f = 1/T
• # of cycles per time unit
• [Frequency] = Hertz (Hz) = t-1
Angular frequency:
• ω = 2πf (units: rad/s)
• ωT = 2π (radians)
• T = 2π / ω
“Phase”: where in the cycle the system is
“Phase constant” or “phase angle”: pick what
part of the cycle is at t = 0
amplitude
Amplitude and phase constant specify the initial conditions for an oscillator
Frequency and amplitude of an oscillator
‰ 11.1. The figures show plots of the amplitude of two harmonic oscillators
versus time. When object B is compared to object A, which of the
following correctly describe the angular frequency and amplitude?
A)
B)
C)
D)
E)
B has larger frequency and larger amplitude than A
B has larger frequency and smaller amplitude than A
B has larger period and larger amplitude than A
B has smaller frequency and smaller amplitude than A
B has larger period and larger amplitude than A
ω = 2πf = 2π/T
x(t ) = x m cos(ωt + ϕ)
4
Hooke’s Law (Spring)Oscillator
F(t ) = − kx(t )
F
F
Restoring force – use Second Law
F(t ) = m a(t) = m
Force equation
∴
d2 x(t )
dt
2
= −
d2 x(t )
dt 2
k
x(t)
m
= − k x(t)
-xm
+xm
No friction losses
Prototype for oscillator
equations describes periodic
motion with resonant frequency:
ω = km
Equations of the form above have sine (or cosine) wave solutions:
x(t ) = x m cos(ωt + ϕ)
Initial condition
examples:
Angular
g
frequency
q
y ω = 2πf = 2π/T
If x(t=0) = xm then phase constant φ = 0, +/- 2π, etc
If x(t=0) = 0 then phase constant φ = π/2, 3π/2, etc
stiff spring / small mass Æ high frequency, short period
big mass / weak spring Æ low frequency, long period
Example: auto suspension trades off spring stiffness against un-sprung weight
Representation of Simple Harmonic Motion…
…as the x-component of a vector rotating at constant speed
displacement
at time t
phase angle
x(t ) = x m cos(ωt + ϕ)
amplitude
r = xm= x(t=0)
phase constant
(radians), equals
zero for sketch
r
ωτ
x(t)
angular frequency
y(t) would be represented as sin(ωt+φ)
velocity at time t
Note :
d(cos[f(t)])
df ( t )
= − sin[ f (t )]
dt
dt
-xm
dx(t )
= − ωx m sin(ωt + ϕ)
dt
sketch shows φ =0
since clock starts
maximum
v
≡
−
ω
x
m
m
when p
phase angle
g =0
velocity
v x (t ) ≡
dv x (t )
= − ω 2 x m cos(ωt + ϕ)
dt
maximum a
acceleration m
T
If φ = π/2, clock starts
at ωt = - π/2
acceleration at time t
a x (t ) ≡
+xm
≡ − ω2xm
d2x(t)
≡ −ω2x(t)
dt2
solutions of
equations like
this oscillate:
5
Motion Equations for Simple Harmonic Motion
A = xmax
•
•
•
x (t ) = A cos (ωt + φ )
dx
v=
= −ω A sin(ω t + φ )
dt
d 2x
a = 2 = −ω 2 A cos(ω t + φ )
dt
Simple harmonic motion is one-dimensional - directions can be
denoted by + or - sign
Simple harmonic motion is not uniformly accelerated motion
The sine and cosine functions oscillate between ±1. The maximum
values of velocity and acceleration for an object in SHM are:
k
A
m
k
= ω2A =
A
m
v max = ω A =
amax
Position and velocity of an oscillator
‰ 11.2. The figure shows the displacement of a harmonic oscillator versus
time. When the motion has progressed to point A on the graph, which of
the following correctly describe the position and velocity?
A)
B)
C)
D)
E)
The position and velocity are both positive
The position and velocity are both negative
The position is negative, the velocity is zero
The position is positive, the velocity is negative
The position is negative, the velocity is positive
x(t ) = x m cos(( ωt + ϕ)
v x (t ) ≡
dx(t )
= − ωx m sin(ωt + ϕ)
dt
6
Example: Spring Oscillator in natural, undamped oscillation
Let k = 65 N/m, xm = 0.11 m at t = 0, m = 0.68 kg
a) Find ω, f, T
x(t ) = x m cos( ωt + ϕ)
ω = k/m = 65 / 0.68 = 9.78 rad / s
f = ω / 2π = 1.56 Hz
v x (t ) = − ωx m sin(ωt + ϕ)
T = 1/f = 0.64 s = 640 ms
a x (t ) = − ω 2 x m cos( ωt + ϕ)
b) Find the amplitude of
f the oscillations
scillati ns
x m = 0.11 m
c) Find the maximum speed and when it is reached
vm = amplitude
of
v(t) = ωx m = 9.78 × 0.11 = 1.1 m/s
at
t = T/4, 3T/4, etc
d) Find the maximum acceleration and when it is reached
am = amplitude
of
a(t) = ω 2 x m = (9.78) 2 × 0.11 = 11 m/s 2
at
t = 0, T/2, same as x(t)
e) Find phase constant
t = 0 : x(t) = x m = x m cos( ϕ ) ⇒ cos( ϕ ) = 1
∴ ϕ = 0, + / - 2π, etc
Match initial conditions at
f) The formula for the motion is:
x(t ) = 0.11 × cos(9.78t + 0)
Energy applied to simple harmonic oscillators
Emech = K + Uel = 2 mv 2x + 2 kx 2
1
F = −kx
Recall:
1
constant if no damping
or forces other than the spring
(Hookes Law restoring force)
xf
W = ∫ Fdx = - Uel =
0
work done in stretching spring from 0 to x f
xf
∴ Uel = (− )(− )k ∫ xdx =
0
1 2
kx f
2
x(t ) = x m cos(ωt + ϕ)
v x (t ) = − ωx m sin(ωt + ϕ)
Oscillator
solutions:
ω 2 = k/m
v x, max = ωx max
where:
Energy:
2
Emech = 2 m(− ωx max ) 2 sin2 (ωt + φ) + 2 kx max
cos 2 (ωt + φ)
1
1
[
2
= 2 kx max
sin2 (ωt + φ) + cos 2 (ωt + φ)
1
]
this always = 1
Result:
1
1
2
Emech = 2 kx max
= 2 mv x2 ,max
for no losses (damping)
7
Energy in SHM
summary
K
x(t ) = A cos (ωt + φ )
dx
= −ω A sin(ω t + φ )
dt
2
d x
a = 2 = −ω 2 A cos(ω t + φ )
dt
v=
Simple Pendulum
U
SHM, small amplitude oscillation of angular coordinate
• Mass m swinging at the end of a massless string
• Angular displacement θ(t) oscillates:
• Gravity provides restoring torque:
• Apply angular
Second Law:
τ = Ια = Ι
no
torque
d2θ( t )
dt
• Solution
oscillates:
displacement
at t
natural frequency
ω≡
d2 θ
dt
2
(force equation)
Ι ≡ mL2
θ3
θ5
sin(θ) = θ −
+
− ..... ≈ θ
3!
5!
mgL
∴ α( t ) ≈ −
θ(t )
mL2
• Apply
A l small
ll θ
approximation:
torque
− θm ≤ θ ≤ + θ m
τ = − m g L sin(θ)
g
L
2
= −
g
θ(t)
L
• Another oscillator equation:
acceleration and displacement
have same time dependence
θ(t ) = θm cos (ωt + φ)
amplitude
period
(radians)
d2x(t)
dt2
≡ −ω2x(t)
phase constant
(radians)
natural angular frequency
2π
T=
= 2π
ω
L
g
no mass dependence!
• Amplitude θm and phase constant φ specify initial state at t = 0…
... If at rest with θ = θm at t = 0, then φ = 0
• alternate: use linear
displacement (arc length):
s(t ) ≡ L θ(t )
a tang (t ) ≡ α(t )L = − (g/L) s(t)
8
Torsion Pendulum
SHM involving angular coordinate
• A restoring torque acts when
disk is twisted from rest:
• Device oscillates
with amplitude:
τ = − κθ
( κ positive)
− θm ≤ θ ≤ + θ m
• Apply Second Law angular):
2
τ = Iα = I
I
d2θ(t )
dt 2
= −
κ
θ(t)
I
d θ
dt 2
• Oscillator equation form:
acceleration and displacement
have same time dependence
• Solution oscillates, as did linear oscillator:
angular displacement
at time t
Natural
frequency
Period
κ
ω≡
Ι
Ι
2π
T=
= 2π
ω
κ
phase constant
(radians)
θ(t ) = θm cos (ωt + φ)
amplitude
(force equation)
natural frequency
No amplitude
dependence!
Does depend on
mass distribution I
Note:
θ(t) = displacement
ωt+φ = “phase”
φ = “phase constant”
9