* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download I I-i1 i1 i2 I-i2 i1
Lumped element model wikipedia , lookup
Integrated circuit wikipedia , lookup
Mathematics of radio engineering wikipedia , lookup
Power electronics wikipedia , lookup
Wien bridge oscillator wikipedia , lookup
Switched-mode power supply wikipedia , lookup
Power MOSFET wikipedia , lookup
Index of electronics articles wikipedia , lookup
Valve RF amplifier wikipedia , lookup
Schmitt trigger wikipedia , lookup
Regenerative circuit wikipedia , lookup
Charlieplexing wikipedia , lookup
Opto-isolator wikipedia , lookup
Surge protector wikipedia , lookup
Two-port network wikipedia , lookup
Operational amplifier wikipedia , lookup
Resistive opto-isolator wikipedia , lookup
Electrical ballast wikipedia , lookup
Rectiverter wikipedia , lookup
RLC circuit wikipedia , lookup
Current mirror wikipedia , lookup
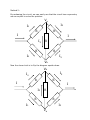
Physics 7B, Lecture 001, Spring 2012 (Xiaosheng Huang) Mid-term 2 – Problem 2 solution Method 1: Using Kirchoff’s current law, we can label the current flowing through each resistor. i1 and i2 are unknown currents that have been introduced. I-i1 R A I-i2 i1-i2 i1 R R R B R i2 C I ε Three loops have also been drawn in the above diagram. Using Kirchoff’s voltage law, we know that the voltage drop around any loop must sum to 0. Loop A: R*i1 + R*(i1-i2) – R*(I-i1) = 0 3i1 – i2 = I Loop B: R*(i1-i2) + R*(I-i2) – R*(i2) = 0 I = 3i2 – i1 If we equate the “I” in both equations: 3i1 – i2 = 3i2 – i1 i1 = i2 Subbing them back into our “I” equations would tell us that i1 = i2 = I/2 Loop C: R*i1 + R*i2 – ε = 0 ε = R*( i1 + i2) = R*I since i1 = i2 = I/2 We also know that the EMF is equal to the total potential drop in the circuit ε = V = Reff * I Hence we immediately see that Reff = R Method 2: By redrawing the circuit, we can easily see that the circuit has a symmetry we can exploit to solve the problem. Va I2 I1 R I R I I3 R R R I4 I5 Vb Now the clever trick is to flip the diagram upside-down. Vb I5 I4 R I R I I3 R R R I1 I2 Va But after the reflection, the assembly of these 5 resistors looks exactly the same as before. Hence they are the same circuit. We see that the direction of the current through the middle resistor (I3) is flipped, so the only way to ensure that both circuit are equivalent is for I3=0 We could have also argued that by symmetry Va=Vb. There is no voltage drop across the middle resistor hence no current flows through it. Since there is no current through the middle resistor, its removal will not affect our circuit. R R R R The effective resistance can be found by summing the resistors in the above diagram, which gives: Reff = R An aside: Symmetry also tells us that I1=I4 and I2=I5. Together with Kirchoff’s junction rule, we can quickly deduce that I1= I2= I4= I5=I/2 with minimal algebra. The lesson is that symmetry is a powerful tool and should be exploited whenever possible!