Download Potential Energy - The Lesson Builder

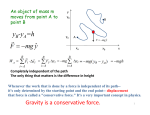
Potential Energy and Conservation of Energy
In conservative systems, we can define another form of energy, based on the configuration of the parts of
the system, which we call potential energy. This quantity is related to work, and thus kinetic energy, through
a simple equation. Using this relation we can finally quantify all mechanical energy, and prove the
conservation of mechanical energy in conservative systems.
Potential Energy
Since mechanical energy must be conserved under conservative forces, but the kinetic energy can fluctuate
based on the speed of the particles in the system, there must be an additional quantity of energy that is a
property of the structure of the system. This quantity, potential energy, is denoted by the symbol U and can
be easily derived from our knowledge of conservative systems.
Consider a system under the action of a conservative force. When work is done on the system it must in
some way change the velocity of its constituent parts (by the Work Energy Theorem), and thus change the
configuration of the system. We define potential energy as the energy of configuration of a conservative
system, and relate it to work in the following way:
ΔU = - W
In other words, work applied by a conservative force reduces the energy of configuration of a system
(potential energy), converting it to kinetic energy.
To see exactly how this conservation works, let's derive the expression for the potential energy of a system
acted upon by gravity. Consider a ball of mass m dropped from a height h. The only force acting upon the
ball is gravity, so we know the system is conservative, since we proved it last section. How much work is
done during the fall? A constant gravitational force of mg acts over a distance of h, so W = mgh . Thus, over
the course of the fall, the potential energy is reduced by a factor of- mgh . We may define the potential
energy to be zero when the ball hits the ground and calculate the potential energy at height h: ΔU = U fU o = - mgh . Thus:
U G = mgh
Since our choice of height h was arbitrary, this equation holds for all h relatively close to the center of the
earth, and the equation is a universal definition of the gravitational potential energy.
An important property of energy is that it is a relative quantity. Just as observers moving with different
velocities observe different values for the kinetic energy of a given particle, observers at a different height
observe different values for gravitational potential energy, for example. When working problems we are free
to choose whatever origin we like, to correspond to a convenient value for our potential energy.
Having defined potential energy, we can now see how it relates to kinetic energy, and generate our principle
of conservation of mechanical energy.
Conservation of Mechanical Energy
We have just established thatΔU = - W , and we know from the Work- Energy Theorem that ΔK = W .
Relating the two equations, we see that ΔU = -ΔK and thus ΔU+ ΔK = 0 . Stated verbally, the sum of the
change in kinetic and potential energy must always equal zero. By the associative property, we can also
write that:
Δ(U+K) = 0
Thus the sum of U and K must be a constant. This constant, denoted by E, is defined as the total
mechanical energy of a conservative system. We can now generate a mathematical expression for the
conservation of mechanical energy:
U+K=E
This statement is true for all conservative systems, and thus for all systems in which U is defined.
With this equation we have completed our proof of the conservation of mechanical energy within
conservative systems. The relation between U, K and E is elegantly simple, and is derived from our
concepts of work, kinetic energy, and conservative forces. Such a relation is also a valuable tool in solving
physical problems. Given an initial state in which we know both K and U, and asked to calculate one of
these quantities in some final state, we simply equate the sums at each state:U o + K o = U f + K f . Such a
relation further bypasses our kinematics laws, and makes calculations in conservative systems quite simple.
Using Calculus to find Potential Energy
Our calculation of the gravitational potential energy was quite easy. Such an easy calculation will not always
be the case, and calculus can be a great help in generating an expression for the potential energy of a
conservative system. Recall that work is defined in calculus as W =
F(x)dx . Thus the change in
potential is simply the negative of this integral.
To demonstrate how to calculate potential energy using vector calculus we shall do so for a mass-spring
system. Consider a mass on a spring, at equilibrium at x = 0 . Recall that the force exerted by the spring,
which is a conservative force, is: F s = - kx , where k is the spring constant. Let us also assign an arbitrary
value to the potential at the equilibrium point: U(0) = 0 . We can now use our relation between potential and
work to find the potential of the system a distance x from the origin:
U(x) - 0 = -
(- kx)dx
Implying that
U(x) =
kx 2
This equation is true for all x. A calculation of the same form can be completed for any conservative system,
and we thus have a universal method for calculating potential energy.
Though Newtonian mechanics provide an axiomatic basis for the study of mechanics, our concept of energy
is more universal: energy applies not only to mechanics, but to electricity, waves, astrophysics, and even
quantum mechanics. Energy pops up again and again in physics, and the conservation of energy remains
one of the fundamental ideas of physics.