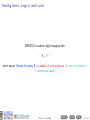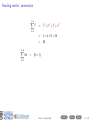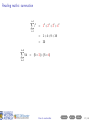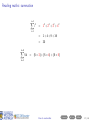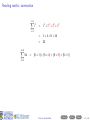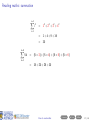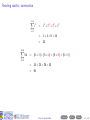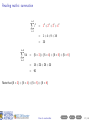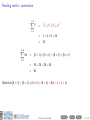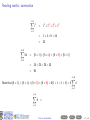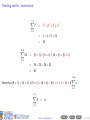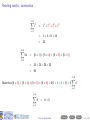Download How to read maths - Current Students

Before you begin
• These slides are used in presentations at workshops.
• They are best viewed with a pdf reader like Acrobat Reader (free download).
• Make sure that “Single Page View” or “Fit to Window” is selected.
• Navigation buttons are provided at the bottom of each screen if needed (see below).
• Viewing in web browsers is not recommended.
Do not try to print the slides
There are many more pages than the number of slides listed at the bottom right of each
screen!
Apologies for any inconvenience.
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
1 / 29
How to read maths
(mα+hs)Smart Workshop
Semester 2, 2016
Geoff Coates
This session demonstrates how to read mathematics (ie. understand shorthand notation)
with examples from MATH1721, MATH1722 and MATH1001 along with sets and
summations.
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
2 / 29
What can (mα+hs)Smart do for you?
Online Stuff
Drop-in Study Sessions
presentation slides from
workshops on many topics
practice exercises
short videos
Monday, Wednesday, Friday,
10am-12pm, Ground Floor
Barry J Marshall Library,
teaching weeks and study
breaks.
and more!
Email: [email protected]
Workshops
Can’t find what you want?
See our current
Workshop Calendar for this
Semester’s topics.
Got a question?
Drop us a line!
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
3 / 29
Contents (page 1 of 2)
The further you go in mathematics, the more skills you need to read lecture notes and
textbooks and the more specialised mathematical writing becomes. Each topic below lists
the units to which it applies.
Go
Sets [all stats units, MATH1001 and higher]
Go
Go
Go
Go
Go
Go
Set notation
Intersection
Union
The empty set
Subsets
Use of sets in maths units
Go
Plus or minus [all maths and stats units]
Go
Factorials [all stats units and turns up in some maths units]
Go
More on next page
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
4 / 29
Contents (page 2 of 2)
The further you go in mathematics, the more skills you need to read lecture notes and
textbooks and the more specialised mathematical writing becomes. Each topic below lists
the units to which it applies.
Go
Summation [very useful for stats units, MATH1721 and higher]
Go
Go
Go
Go
“Drilling down” [a useful study method for complicated topics]
Go
Go
Go
Examples
An example from MATH1721/MATH1722
A brain teaser!
Example from MATH1001
Final comments
Appendix: number sets [MATH1721 and higher]
Go
Go
Go
Go
Natural numbers, whole numbers and integers
Rational numbers
Irrational numbers
Real numbers
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
5 / 29
Reading maths
Mathematical writing is a language. It just contains a lot of shorthand (ie. notation) in
place of lots of words.
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
6 / 29
Reading maths
Mathematical writing is a language. It just contains a lot of shorthand (ie. notation) in
place of lots of words.
Train yourself to read out all the words (at least until you understand the topic)
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
6 / 29
Reading maths
Mathematical writing is a language. It just contains a lot of shorthand (ie. notation) in
place of lots of words.
Train yourself to read out all the words (at least until you understand the topic) and learn
to “read between the lines” (ie. make use of context).
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
6 / 29
Reading maths
Mathematical writing is a language. It just contains a lot of shorthand (ie. notation) in
place of lots of words.
Train yourself to read out all the words (at least until you understand the topic) and learn
to “read between the lines” (ie. make use of context).
Here are some examples.
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
6 / 29
Reading maths: set notation
X = {4, 5, 6, 7, 8}
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
7 / 29
Reading maths: set notation
X = {4, 5, 6, 7, 8}
We read this as:
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
7 / 29
Reading maths: set notation
X = {4, 5, 6, 7, 8}
We read this as: “X
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
7 / 29
Reading maths: set notation
X = {4, 5, 6, 7, 8}
We read this as: “X is the name of
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
7 / 29
Reading maths: set notation
X = {4, 5, 6, 7, 8}
We read this as: “X is the name of the set containing
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
7 / 29
Reading maths: set notation
X = {4, 5, 6, 7, 8}
We read this as: “X is the name of the set containing the numbers (or elements) 4, 5, 6,
7 and 8”.
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
7 / 29
Reading maths: set notation
X = {4, 5, 6, 7, 8}
We read this as: “X is the name of the set containing the numbers (or elements) 4, 5, 6,
7 and 8”.
Here we have shorthand within shorthand!
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
7 / 29
Reading maths: set notation
X = {4, 5, 6, 7, 8}
We read this as: “X is the name of the set containing the numbers (or elements) 4, 5, 6,
7 and 8”.
Here we have shorthand within shorthand! The capital letter X is used as a shorthand (or
name) for the set {4, 5, 6, 7, 8}.
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
7 / 29
Reading maths: set notation
X = {4, 5, 6, 7, 8}
We read this as: “X is the name of the set containing the numbers (or elements) 4, 5, 6,
7 and 8”.
Here we have shorthand within shorthand! The capital letter X is used as a shorthand (or
name) for the set {4, 5, 6, 7, 8}.
What does this statement say? 4 ∈ X
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
7 / 29
Reading maths: set notation
X = {4, 5, 6, 7, 8}
We read this as: “X is the name of the set containing the numbers (or elements) 4, 5, 6,
7 and 8”.
Here we have shorthand within shorthand! The capital letter X is used as a shorthand (or
name) for the set {4, 5, 6, 7, 8}.
What does this statement say? 4 ∈ X
“4
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
7 / 29
Reading maths: set notation
X = {4, 5, 6, 7, 8}
We read this as: “X is the name of the set containing the numbers (or elements) 4, 5, 6,
7 and 8”.
Here we have shorthand within shorthand! The capital letter X is used as a shorthand (or
name) for the set {4, 5, 6, 7, 8}.
What does this statement say? 4 ∈ X
“4 is an element of
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
7 / 29
Reading maths: set notation
X = {4, 5, 6, 7, 8}
We read this as: “X is the name of the set containing the numbers (or elements) 4, 5, 6,
7 and 8”.
Here we have shorthand within shorthand! The capital letter X is used as a shorthand (or
name) for the set {4, 5, 6, 7, 8}.
What does this statement say? 4 ∈ X
“4 is an element of the set X ”.
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
7 / 29
Reading maths: set notation
X = {4, 5, 6, 7, 8}
We read this as: “X is the name of the set containing the numbers (or elements) 4, 5, 6,
7 and 8”.
Here we have shorthand within shorthand! The capital letter X is used as a shorthand (or
name) for the set {4, 5, 6, 7, 8}.
What does this statement say? 4 ∈ X
“4 is an element of the set X ”.
What about this one? 97 ∈
/X
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
7 / 29
Reading maths: set notation
X = {4, 5, 6, 7, 8}
We read this as: “X is the name of the set containing the numbers (or elements) 4, 5, 6,
7 and 8”.
Here we have shorthand within shorthand! The capital letter X is used as a shorthand (or
name) for the set {4, 5, 6, 7, 8}.
What does this statement say? 4 ∈ X
“4 is an element of the set X ”.
What about this one? 97 ∈
/X
“97
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
7 / 29
Reading maths: set notation
X = {4, 5, 6, 7, 8}
We read this as: “X is the name of the set containing the numbers (or elements) 4, 5, 6,
7 and 8”.
Here we have shorthand within shorthand! The capital letter X is used as a shorthand (or
name) for the set {4, 5, 6, 7, 8}.
What does this statement say? 4 ∈ X
“4 is an element of the set X ”.
What about this one? 97 ∈
/X
“97 is not an element of
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
7 / 29
Reading maths: set notation
X = {4, 5, 6, 7, 8}
We read this as: “X is the name of the set containing the numbers (or elements) 4, 5, 6,
7 and 8”.
Here we have shorthand within shorthand! The capital letter X is used as a shorthand (or
name) for the set {4, 5, 6, 7, 8}.
What does this statement say? 4 ∈ X
“4 is an element of the set X ”.
What about this one? 97 ∈
/X
“97 is not an element of the set X ”.
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
7 / 29
Reading maths: set notation: intersection
Just like with numbers, we can combine two or more sets in certain ways to get a new set.
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
8 / 29
Reading maths: set notation: intersection
Just like with numbers, we can combine two or more sets in certain ways to get a new set.
What does this mean? A ∩ B
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
8 / 29
Reading maths: set notation: intersection
Just like with numbers, we can combine two or more sets in certain ways to get a new set.
What does this mean? A ∩ B
“The intersection of two sets A and B” (ie. the set of all elements which are common to
both A and B.
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
8 / 29
Reading maths: set notation: intersection
Just like with numbers, we can combine two or more sets in certain ways to get a new set.
What does this mean? A ∩ B
“The intersection of two sets A and B” (ie. the set of all elements which are common to
both A and B.
e.g A = {1, 2, 3, 4, 5, 6}, B = {2, 4, 6, 8, 10}.
A∩B ={
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
8 / 29
Reading maths: set notation: intersection
Just like with numbers, we can combine two or more sets in certain ways to get a new set.
What does this mean? A ∩ B
“The intersection of two sets A and B” (ie. the set of all elements which are common to
both A and B.
e.g A = {1, 2, 3, 4, 5, 6}, B = {2, 4, 6, 8, 10}.
A∩B ={
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
8 / 29
Reading maths: set notation: intersection
Just like with numbers, we can combine two or more sets in certain ways to get a new set.
What does this mean? A ∩ B
“The intersection of two sets A and B” (ie. the set of all elements which are common to
both A and B.
e.g A = {1, 2, 3, 4, 5, 6}, B = {2, 4, 6, 8, 10}.
A ∩ B = {2,
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
8 / 29
Reading maths: set notation: intersection
Just like with numbers, we can combine two or more sets in certain ways to get a new set.
What does this mean? A ∩ B
“The intersection of two sets A and B” (ie. the set of all elements which are common to
both A and B.
e.g A = {1, 2, 3, 4, 5, 6}, B = {2, 4, 6, 8, 10}.
A ∩ B = {2,
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
8 / 29
Reading maths: set notation: intersection
Just like with numbers, we can combine two or more sets in certain ways to get a new set.
What does this mean? A ∩ B
“The intersection of two sets A and B” (ie. the set of all elements which are common to
both A and B.
e.g A = {1, 2, 3, 4, 5, 6}, B = {2, 4, 6, 8, 10}.
A ∩ B = {2, 4,
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
8 / 29
Reading maths: set notation: intersection
Just like with numbers, we can combine two or more sets in certain ways to get a new set.
What does this mean? A ∩ B
“The intersection of two sets A and B” (ie. the set of all elements which are common to
both A and B.
e.g A = {1, 2, 3, 4, 5, 6}, B = {2, 4, 6, 8, 10}.
A ∩ B = {2, 4,
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
8 / 29
Reading maths: set notation: intersection
Just like with numbers, we can combine two or more sets in certain ways to get a new set.
What does this mean? A ∩ B
“The intersection of two sets A and B” (ie. the set of all elements which are common to
both A and B.
e.g A = {1, 2, 3, 4, 5, 6}, B = {2, 4, 6, 8, 10}.
A ∩ B = {2, 4, 6
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
8 / 29
Reading maths: set notation: intersection
Just like with numbers, we can combine two or more sets in certain ways to get a new set.
What does this mean? A ∩ B
“The intersection of two sets A and B” (ie. the set of all elements which are common to
both A and B.
e.g A = {1, 2, 3, 4, 5, 6}, B = {2, 4, 6, 8, 10}.
A ∩ B = {2, 4, 6}
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
8 / 29
Reading maths: set notation: union
What does this mean? A ∪ B
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
9 / 29
Reading maths: set notation: union
What does this mean? A ∪ B
“The union of two sets A and B” (ie. the set of all elements which are in either A or B
or both).
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
9 / 29
Reading maths: set notation: union
What does this mean? A ∪ B
“The union of two sets A and B” (ie. the set of all elements which are in either A or B
or both).
e.g A = {1, 2, 3, 4, 5, 6}, B = {2, 4, 6, 8, 10}.
A∪B ={
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
9 / 29
Reading maths: set notation: union
What does this mean? A ∪ B
“The union of two sets A and B” (ie. the set of all elements which are in either A or B
or both).
e.g A = {1, 2, 3, 4, 5, 6}, B = {2, 4, 6, 8, 10}.
A∪B ={
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
9 / 29
Reading maths: set notation: union
What does this mean? A ∪ B
“The union of two sets A and B” (ie. the set of all elements which are in either A or B
or both).
e.g A = {1, 2, 3, 4, 5, 6}, B = {2, 4, 6, 8, 10}.
A ∪ B = {1, 2, 3, 4, 5, 6
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
9 / 29
Reading maths: set notation: union
What does this mean? A ∪ B
“The union of two sets A and B” (ie. the set of all elements which are in either A or B
or both).
e.g A = {1, 2, 3, 4, 5, 6}, B = {2, 4, 6, 8, 10}.
A ∪ B = {1, 2, 3, 4, 5, 6
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
9 / 29
Reading maths: set notation: union
What does this mean? A ∪ B
“The union of two sets A and B” (ie. the set of all elements which are in either A or B
or both).
e.g A = {1, 2, 3, 4, 5, 6}, B = {2, 4, 6, 8, 10}.
A ∪ B = {1, 2, 3, 4, 5, 6, 8, 10}
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
9 / 29
Reading maths: set notation: union
What does this mean? A ∪ B
“The union of two sets A and B” (ie. the set of all elements which are in either A or B
or both).
e.g A = {1, 2, 3, 4, 5, 6}, B = {2, 4, 6, 8, 10}.
A ∪ B = {1, 2, 3, 4, 5, 6, 8, 10}
Note: We do not repeat elements in a set.
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
9 / 29
Reading maths: set notation: the empty set
Sometimes, two sets have nothing in common. This means that their intersection would
be a set with nothing in it! We call this the empty set.
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
10 / 29
Reading maths: set notation: the empty set
Sometimes, two sets have nothing in common. This means that their intersection would
be a set with nothing in it! We call this the empty set.
The empty set looks like {}. We usually denote this by ∅.
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
10 / 29
Reading maths: set notation: the empty set
Sometimes, two sets have nothing in common. This means that their intersection would
be a set with nothing in it! We call this the empty set.
The empty set looks like {}. We usually denote this by ∅.
e.g A = {1, 2, 3, 4, 5}, B = {6, 7, 8, 9, 10}.
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
10 / 29
Reading maths: set notation: the empty set
Sometimes, two sets have nothing in common. This means that their intersection would
be a set with nothing in it! We call this the empty set.
The empty set looks like {}. We usually denote this by ∅.
e.g A = {1, 2, 3, 4, 5}, B = {6, 7, 8, 9, 10}.
Here we have that A ∩ B = ∅.
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
10 / 29
Reading maths: set notation: subsets
Sometimes, we find that sets are contained in other sets.
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
11 / 29
Reading maths: set notation: subsets
Sometimes, we find that sets are contained in other sets.
Example: Consider the two sets J = {1, 3, 5} and K = {1, 2, 3, 4, 5}.
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
11 / 29
Reading maths: set notation: subsets
Sometimes, we find that sets are contained in other sets.
Example: Consider the two sets J = {1, 3, 5} and K = {1, 2, 3, 4, 5}.
It is clear that every element in J is also in K .
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
11 / 29
Reading maths: set notation: subsets
Sometimes, we find that sets are contained in other sets.
Example: Consider the two sets J = {1, 3, 5} and K = {1, 2, 3, 4, 5}.
It is clear that every element in J is also in K .
So “J is contained inside K ”. We write this as “J ⊂ K ”.
and we say that J is a subset of K .
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
11 / 29
Reading maths: usage in maths units
MATH1001 students might recognise this:
“ S ⊆ Rn ”
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
12 / 29
Reading maths: usage in maths units
MATH1001 students might recognise this:
“ S ⊆ Rn ”
which means “the set of vectors S is a subset of, or the same as, the set of all vectors in
n−dimensional space”.
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
12 / 29
Reading maths: usage in maths units
When working with numbers, we might want to specify all of the integers which square
to a number less than or equal to 25.
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
13 / 29
Reading maths: usage in maths units
When working with numbers, we might want to specify all of the integers which square
to a number less than or equal to 25.
We write this as:
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
13 / 29
Reading maths: usage in maths units
When working with numbers, we might want to specify all of the integers which square
to a number less than or equal to 25.
We write this as:
{ m ∈ Z | m2 ≤ 25 }
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
13 / 29
Reading maths: usage in maths units
When working with numbers, we might want to specify all of the integers which square
to a number less than or equal to 25.
We write this as:
{ m ∈ Z | m2 ≤ 25 }
which reads as
“the set of
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
13 / 29
Reading maths: usage in maths units
When working with numbers, we might want to specify all of the integers which square
to a number less than or equal to 25.
We write this as:
{ m ∈ Z | m2 ≤ 25 }
which reads as
“the set of all integers m
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
13 / 29
Reading maths: usage in maths units
When working with numbers, we might want to specify all of the integers which square
to a number less than or equal to 25.
We write this as:
{ m ∈ Z | m2 ≤ 25 }
which reads as
“the set of all integers m such that
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
13 / 29
Reading maths: usage in maths units
When working with numbers, we might want to specify all of the integers which square
to a number less than or equal to 25.
We write this as:
{ m ∈ Z | m2 ≤ 25 }
which reads as
“the set of all integers m such that the square of m is less than or equal to 25”.
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
13 / 29
Reading maths: usage in maths units
When working with numbers, we might want to specify all of the integers which square
to a number less than or equal to 25.
We write this as:
{ m ∈ Z | m2 ≤ 25 }
which reads as
“the set of all integers m such that the square of m is less than or equal to 25”.
Note: You can use any suitable letter for the variable name, eg:
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
13 / 29
Reading maths: usage in maths units
When working with numbers, we might want to specify all of the integers which square
to a number less than or equal to 25.
We write this as:
{ m ∈ Z | m2 ≤ 25 }
which reads as
“the set of all integers m such that the square of m is less than or equal to 25”.
Note: You can use any suitable letter for the variable name, eg:
{ t ∈ Z | t 2 ≤ 25 }
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
13 / 29
Reading maths: usage in maths units
When working with numbers, we might want to specify all of the integers which square
to a number less than or equal to 25.
We write this as:
{ m ∈ Z | m2 ≤ 25 }
which reads as
“the set of all integers m such that the square of m is less than or equal to 25”.
Note: You can use any suitable letter for the variable name, eg:
{ t ∈ Z | t 2 ≤ 25 }
The elements of this particular set can be written out individually:
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
13 / 29
Reading maths: usage in maths units
When working with numbers, we might want to specify all of the integers which square
to a number less than or equal to 25.
We write this as:
{ m ∈ Z | m2 ≤ 25 }
which reads as
“the set of all integers m such that the square of m is less than or equal to 25”.
Note: You can use any suitable letter for the variable name, eg:
{ t ∈ Z | t 2 ≤ 25 }
The elements of this particular set can be written out individually:
{−5, −4, −3, −2, −1, 0, 1, 2, 3, 4, 5}
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
13 / 29
Reading maths: plus or minus
We can use the symbol ± (plus or minus) to represent two numbers at the same time.
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
14 / 29
Reading maths: plus or minus
We can use the symbol ± (plus or minus) to represent two numbers at the same time.
e.g. 3 ± 2 represents both 5 (which is 3 + 2) and 1 (which is 3 − 2).
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
14 / 29
Reading maths: plus or minus
We can use the symbol ± (plus or minus) to represent two numbers at the same time.
e.g. 3 ± 2 represents both 5 (which is 3 + 2) and 1 (which is 3 − 2).
e.g. 5 ± 8 represents
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
14 / 29
Reading maths: plus or minus
We can use the symbol ± (plus or minus) to represent two numbers at the same time.
e.g. 3 ± 2 represents both 5 (which is 3 + 2) and 1 (which is 3 − 2).
e.g. 5 ± 8 represents both 13 (which is 5 + 8) and −3 (which is 5 − 8).
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
14 / 29
Reading maths: factorials
The factorial of a natural number is the product of all the natural numbers less than or
equal to it. We denote the factorial with an exclamation mark (!).
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
15 / 29
Reading maths: factorials
The factorial of a natural number is the product of all the natural numbers less than or
equal to it. We denote the factorial with an exclamation mark (!).
2! = 2 × 1 = 2
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
15 / 29
Reading maths: factorials
The factorial of a natural number is the product of all the natural numbers less than or
equal to it. We denote the factorial with an exclamation mark (!).
2! = 2 × 1 = 2
3! = 3 × 2 × 1 = 6
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
15 / 29
Reading maths: factorials
The factorial of a natural number is the product of all the natural numbers less than or
equal to it. We denote the factorial with an exclamation mark (!).
2! = 2 × 1 = 2
3! = 3 × 2 × 1 = 6
4! = 4 × 3 × 2 × 1 = 24
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
15 / 29
Reading maths: factorials
The factorial of a natural number is the product of all the natural numbers less than or
equal to it. We denote the factorial with an exclamation mark (!).
2! = 2 × 1 = 2
3! = 3 × 2 × 1 = 6
4! = 4 × 3 × 2 × 1 = 24
5! = 5 × 4 × 3 × 2 × 1 = 120
..
.
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
15 / 29
Reading maths: factorials
The factorial of a natural number is the product of all the natural numbers less than or
equal to it. We denote the factorial with an exclamation mark (!).
1! = 1
2! = 2 × 1 = 2
3! = 3 × 2 × 1 = 6
4! = 4 × 3 × 2 × 1 = 24
5! = 5 × 4 × 3 × 2 × 1 = 120
..
.
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
15 / 29
Reading maths: factorials
The factorial of a natural number is the product of all the natural numbers less than or
equal to it. We denote the factorial with an exclamation mark (!).
1! = 1
2! = 2 × 1 = 2
3! = 3 × 2 × 1 = 6
4! = 4 × 3 × 2 × 1 = 24
5! = 5 × 4 × 3 × 2 × 1 = 120
..
.
12! = 12 × 11 × 10 × 9 × 8 × 7 × 6 × 5 × 4 × 3 × 2 × 1 = 479, 001, 600
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
15 / 29
Reading maths: factorials
The factorial of a natural number is the product of all the natural numbers less than or
equal to it. We denote the factorial with an exclamation mark (!).
1! = 1
2! = 2 × 1 = 2
3! = 3 × 2 × 1 = 6
4! = 4 × 3 × 2 × 1 = 24
5! = 5 × 4 × 3 × 2 × 1 = 120
..
.
12! = 12 × 11 × 10 × 9 × 8 × 7 × 6 × 5 × 4 × 3 × 2 × 1 = 479, 001, 600
Factorials get very big very fast!
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
15 / 29
Reading maths: summation
Sometimes we want a concise way to represent the addition of a specific set of objects
(usually numbers, vectors, terms in a matrix).
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
16 / 29
Reading maths: summation
Sometimes we want a concise way to represent the addition of a specific set of objects
(usually numbers, vectors, terms in a matrix).
If we want to “add up all the whole numbers from 1 to 5” we write:
n=5
X
n
n=1
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
16 / 29
Reading maths: summation
Sometimes we want a concise way to represent the addition of a specific set of objects
(usually numbers, vectors, terms in a matrix).
If we want to “add up all the whole numbers from 1 to 5” we write:
n=5
X
n=1
n=1
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
16 / 29
Reading maths: summation
Sometimes we want a concise way to represent the addition of a specific set of objects
(usually numbers, vectors, terms in a matrix).
If we want to “add up all the whole numbers from 1 to 5” we write:
n=5
X
n =1+2
n=1
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
16 / 29
Reading maths: summation
Sometimes we want a concise way to represent the addition of a specific set of objects
(usually numbers, vectors, terms in a matrix).
If we want to “add up all the whole numbers from 1 to 5” we write:
n=5
X
n =1+2+3+4
n=1
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
16 / 29
Reading maths: summation
Sometimes we want a concise way to represent the addition of a specific set of objects
(usually numbers, vectors, terms in a matrix).
If we want to “add up all the whole numbers from 1 to 5” we write:
n=5
X
n =1+2+3+4+5
n=1
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
16 / 29
Reading maths: summation
Sometimes we want a concise way to represent the addition of a specific set of objects
(usually numbers, vectors, terms in a matrix).
If we want to “add up all the whole numbers from 1 to 5” we write:
n=5
X
n = 1 + 2 + 3 + 4 + 5 = 15
n=1
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
16 / 29
Reading maths: summation
Sometimes we want a concise way to represent the addition of a specific set of objects
(usually numbers, vectors, terms in a matrix).
If we want to “add up all the whole numbers from 1 to 5” we write:
n=5
X
n = 1 + 2 + 3 + 4 + 5 = 15
n=1
P
is the capital form of the greek letter sigma and represents the act of “adding up”.
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
16 / 29
Reading maths: summation
Sometimes we want a concise way to represent the addition of a specific set of objects
(usually numbers, vectors, terms in a matrix).
If we want to “add up all the whole numbers from 1 to 5” we write:
n=5
X
n = 1 + 2 + 3 + 4 + 5 = 15
n=1
P
is the capital form of the greek letter sigma and represents the act of “adding up”.
Below it we state the starting point of n, above it we state the finishing point of n.
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
16 / 29
Reading maths: summation
Sometimes we want a concise way to represent the addition of a specific set of objects
(usually numbers, vectors, terms in a matrix).
If we want to “add up all the whole numbers from 1 to 5” we write:
n=5
X
n = 1 + 2 + 3 + 4 + 5 = 15
n=1
P
is the capital form of the greek letter sigma and represents the act of “adding up”.
Below it we state the starting point of n, above it we state the finishing point of n.
So, wherever n appears in the expression being summed we first replace it with n = 1,
then n = 2 and so on up to n = 5. Each of these five numbers are then added together.
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
16 / 29
Reading maths: summation
Sometimes we want a concise way to represent the addition of a specific set of objects
(usually numbers, vectors, terms in a matrix).
If we want to “add up all the whole numbers from 1 to 5” we write:
n=5
X
n = 1 + 2 + 3 + 4 + 5 = 15
n=1
P
is the capital form of the greek letter sigma and represents the act of “adding up”.
Below it we state the starting point of n, above it we state the finishing point of n.
So, wherever n appears in the expression being summed we first replace it with n = 1,
then n = 2 and so on up to n = 5. Each of these five numbers are then added together.
Note: i is a “dummy” variable. It does not appear in the final answer. Each of these
sums would give the same answer:
i=5
X
i
i=1
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
16 / 29
Reading maths: summation
Sometimes we want a concise way to represent the addition of a specific set of objects
(usually numbers, vectors, terms in a matrix).
If we want to “add up all the whole numbers from 1 to 5” we write:
n=5
X
n = 1 + 2 + 3 + 4 + 5 = 15
n=1
P
is the capital form of the greek letter sigma and represents the act of “adding up”.
Below it we state the starting point of n, above it we state the finishing point of n.
So, wherever n appears in the expression being summed we first replace it with n = 1,
then n = 2 and so on up to n = 5. Each of these five numbers are then added together.
Note: i is a “dummy” variable. It does not appear in the final answer. Each of these
sums would give the same answer:
i=5
X
i=1
i
p=5
X
p
p=1
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
16 / 29
Reading maths: summation
Sometimes we want a concise way to represent the addition of a specific set of objects
(usually numbers, vectors, terms in a matrix).
If we want to “add up all the whole numbers from 1 to 5” we write:
n=5
X
n = 1 + 2 + 3 + 4 + 5 = 15
n=1
P
is the capital form of the greek letter sigma and represents the act of “adding up”.
Below it we state the starting point of n, above it we state the finishing point of n.
So, wherever n appears in the expression being summed we first replace it with n = 1,
then n = 2 and so on up to n = 5. Each of these five numbers are then added together.
Note: i is a “dummy” variable. It does not appear in the final answer. Each of these
sums would give the same answer:
i=5
X
i=1
i
p=5
X
p
p=1
((mα+hs)Smart
How
Workshop
to read
Semester
maths
θ=5
X
θ
θ=1
2, 2016)
Contents
Prev
Next
16 / 29
Reading maths: summation
i=4
X
i2
i=1
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
17 / 29
Reading maths: summation
i=4
X
i2
i=1
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
17 / 29
Reading maths: summation
i=4
X
i2
=
12
i=1
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
17 / 29
Reading maths: summation
i=4
X
i2
=
12 + 2 2
i=1
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
17 / 29
Reading maths: summation
i=4
X
i2
=
12 + 2 2 + 3 2
i=1
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
17 / 29
Reading maths: summation
i=4
X
i2
=
12 + 2 2 + 3 2 + 4 2
i=1
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
17 / 29
Reading maths: summation
i=4
X
i2
=
12 + 2 2 + 3 2 + 4 2
=
1 + 4 + 9 + 16
i=1
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
17 / 29
Reading maths: summation
i=4
X
i2
=
12 + 2 2 + 3 2 + 4 2
=
1 + 4 + 9 + 16
=
30
i=1
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
17 / 29
Reading maths: summation
i=4
X
i2
=
12 + 2 2 + 3 2 + 4 2
=
1 + 4 + 9 + 16
=
30
i=1
k=6
X
5k
=
k=3
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
17 / 29
Reading maths: summation
i=4
X
i2
=
12 + 2 2 + 3 2 + 4 2
=
1 + 4 + 9 + 16
=
30
i=1
k=6
X
5k
=
k=3
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
17 / 29
Reading maths: summation
i=4
X
i2
=
12 + 2 2 + 3 2 + 4 2
=
1 + 4 + 9 + 16
=
30
i=1
k=6
X
5k
=
(5 × 3)
k=3
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
17 / 29
Reading maths: summation
i=4
X
i2
=
12 + 2 2 + 3 2 + 4 2
=
1 + 4 + 9 + 16
=
30
i=1
k=6
X
5k
=
(5 × 3) + (5 × 4)
k=3
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
17 / 29
Reading maths: summation
i=4
X
i2
=
12 + 2 2 + 3 2 + 4 2
=
1 + 4 + 9 + 16
=
30
i=1
k=6
X
5k
=
(5 × 3) + (5 × 4) + (5 × 5)
k=3
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
17 / 29
Reading maths: summation
i=4
X
i2
=
12 + 2 2 + 3 2 + 4 2
=
1 + 4 + 9 + 16
=
30
i=1
k=6
X
5k
=
(5 × 3) + (5 × 4) + (5 × 5) + (5 × 6)
k=3
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
17 / 29
Reading maths: summation
i=4
X
i2
=
12 + 2 2 + 3 2 + 4 2
=
1 + 4 + 9 + 16
=
30
i=1
k=6
X
5k
=
(5 × 3) + (5 × 4) + (5 × 5) + (5 × 6)
=
15 + 20 + 25 + 30
k=3
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
17 / 29
Reading maths: summation
i=4
X
i2
=
12 + 2 2 + 3 2 + 4 2
=
1 + 4 + 9 + 16
=
30
i=1
k=6
X
5k
=
(5 × 3) + (5 × 4) + (5 × 5) + (5 × 6)
=
15 + 20 + 25 + 30
=
90
k=3
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
17 / 29
Reading maths: summation
i=4
X
i2
=
12 + 2 2 + 3 2 + 4 2
=
1 + 4 + 9 + 16
=
30
i=1
k=6
X
5k
=
(5 × 3) + (5 × 4) + (5 × 5) + (5 × 6)
=
15 + 20 + 25 + 30
=
90
k=3
Note that (5 × 3) + (5 × 4) + (5 × 5) + (5 × 6)
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
17 / 29
Reading maths: summation
i=4
X
i2
=
12 + 2 2 + 3 2 + 4 2
=
1 + 4 + 9 + 16
=
30
i=1
k=6
X
5k
=
(5 × 3) + (5 × 4) + (5 × 5) + (5 × 6)
=
15 + 20 + 25 + 30
=
90
k=3
Note that (5 × 3) + (5 × 4) + (5 × 5) + (5 × 6) = 5(3 + 4 + 5 + 6)
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
17 / 29
Reading maths: summation
i=4
X
i2
=
12 + 2 2 + 3 2 + 4 2
=
1 + 4 + 9 + 16
=
30
i=1
k=6
X
5k
=
(5 × 3) + (5 × 4) + (5 × 5) + (5 × 6)
=
15 + 20 + 25 + 30
=
90
k=3
Note that (5 × 3) + (5 × 4) + (5 × 5) + (5 × 6) = 5(3 + 4 + 5 + 6) = 5
k=6
X
k
k=3
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
17 / 29
Reading maths: summation
i=4
X
i2
=
12 + 2 2 + 3 2 + 4 2
=
1 + 4 + 9 + 16
=
30
i=1
k=6
X
5k
=
(5 × 3) + (5 × 4) + (5 × 5) + (5 × 6)
=
15 + 20 + 25 + 30
=
90
k=3
Note that (5 × 3) + (5 × 4) + (5 × 5) + (5 × 6) = 5(3 + 4 + 5 + 6) = 5
k=6
X
k
k=3
j=4
X
6
=
j=1
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
17 / 29
Reading maths: summation
i=4
X
i2
=
12 + 2 2 + 3 2 + 4 2
=
1 + 4 + 9 + 16
=
30
i=1
k=6
X
5k
=
(5 × 3) + (5 × 4) + (5 × 5) + (5 × 6)
=
15 + 20 + 25 + 30
=
90
k=3
Note that (5 × 3) + (5 × 4) + (5 × 5) + (5 × 6) = 5(3 + 4 + 5 + 6) = 5
k=6
X
k
k=3
j=4
X
6
=
6
j=1
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
17 / 29
Reading maths: summation
i=4
X
i2
=
12 + 2 2 + 3 2 + 4 2
=
1 + 4 + 9 + 16
=
30
i=1
k=6
X
5k
=
(5 × 3) + (5 × 4) + (5 × 5) + (5 × 6)
=
15 + 20 + 25 + 30
=
90
k=3
Note that (5 × 3) + (5 × 4) + (5 × 5) + (5 × 6) = 5(3 + 4 + 5 + 6) = 5
k=6
X
k
k=3
j=4
X
6
=
6+6
j=1
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
17 / 29
Reading maths: summation
i=4
X
i2
=
12 + 2 2 + 3 2 + 4 2
=
1 + 4 + 9 + 16
=
30
i=1
k=6
X
5k
=
(5 × 3) + (5 × 4) + (5 × 5) + (5 × 6)
=
15 + 20 + 25 + 30
=
90
k=3
Note that (5 × 3) + (5 × 4) + (5 × 5) + (5 × 6) = 5(3 + 4 + 5 + 6) = 5
k=6
X
k
k=3
j=4
X
6
=
6+6+6
j=1
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
17 / 29
Reading maths: summation
i=4
X
i2
=
12 + 2 2 + 3 2 + 4 2
=
1 + 4 + 9 + 16
=
30
i=1
k=6
X
5k
=
(5 × 3) + (5 × 4) + (5 × 5) + (5 × 6)
=
15 + 20 + 25 + 30
=
90
k=3
Note that (5 × 3) + (5 × 4) + (5 × 5) + (5 × 6) = 5(3 + 4 + 5 + 6) = 5
k=6
X
k
k=3
j=4
X
6
=
6+6+6+6
j=1
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
17 / 29
Reading maths: summation
i=4
X
i2
=
12 + 2 2 + 3 2 + 4 2
=
1 + 4 + 9 + 16
=
30
i=1
k=6
X
5k
=
(5 × 3) + (5 × 4) + (5 × 5) + (5 × 6)
=
15 + 20 + 25 + 30
=
90
k=3
Note that (5 × 3) + (5 × 4) + (5 × 5) + (5 × 6) = 5(3 + 4 + 5 + 6) = 5
k=6
X
k
k=3
j=4
X
6
=
6+6+6+6
=
24
j=1
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
17 / 29
Reading maths: summation: MATH1721/MATH1722 example
In MATH1721 and MATH1722 there is a general description of a polynomial function:
f (x ) = a0 + a1 x 1 + a2 x 2 + . . . + an−1 x n−1 + an x n
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
18 / 29
Reading maths: summation: MATH1721/MATH1722 example
In MATH1721 and MATH1722 there is a general description of a polynomial function:
f (x ) = a0 + a1 x 1 + a2 x 2 + . . . + an−1 x n−1 + an x n
Q: What do the superscripts on the x ’s mean?
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
18 / 29
Reading maths: summation: MATH1721/MATH1722 example
In MATH1721 and MATH1722 there is a general description of a polynomial function:
f (x ) = a0 + a1 x 1 + a2 x 2 + . . . + an−1 x n−1 + an x n
Q: What do the superscripts on the x ’s mean?
A: Powers of the variable x .
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
18 / 29
Reading maths: summation: MATH1721/MATH1722 example
In MATH1721 and MATH1722 there is a general description of a polynomial function:
f (x ) = a0 + a1 x 1 + a2 x 2 + . . . + an−1 x n−1 + an x n
Q: What do the superscripts on the x ’s mean?
A: Powers of the variable x .
Q: Why is x a variable (as opposed to a fixed number or constant)?
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
18 / 29
Reading maths: summation: MATH1721/MATH1722 example
In MATH1721 and MATH1722 there is a general description of a polynomial function:
f (x ) = a0 + a1 x 1 + a2 x 2 + . . . + an−1 x n−1 + an x n
Q: What do the superscripts on the x ’s mean?
A: Powers of the variable x .
Q: Why is x a variable (as opposed to a fixed number or constant)?
A: It appears in the brackets after f so the output variable f is a function of the input
variable x .
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
18 / 29
Reading maths: summation: MATH1721/MATH1722 example
In MATH1721 and MATH1722 there is a general description of a polynomial function:
f (x ) = a0 + a1 x 1 + a2 x 2 + . . . + an−1 x n−1 + an x n
Q: What do the superscripts on the x ’s mean?
A: Powers of the variable x .
Q: Why is x a variable (as opposed to a fixed number or constant)?
A: It appears in the brackets after f so the output variable f is a function of the input
variable x .
Q: What do the subscripts on the a’s mean?
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
18 / 29
Reading maths: summation: MATH1721/MATH1722 example
In MATH1721 and MATH1722 there is a general description of a polynomial function:
f (x ) = a0 + a1 x 1 + a2 x 2 + . . . + an−1 x n−1 + an x n
Q: What do the superscripts on the x ’s mean?
A: Powers of the variable x .
Q: Why is x a variable (as opposed to a fixed number or constant)?
A: It appears in the brackets after f so the output variable f is a function of the input
variable x .
Q: What do the subscripts on the a’s mean?
A: They are just labels to distinguish one arbitrary number or constant from another.
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
18 / 29
Reading maths: summation: MATH1721/MATH1722 example
In MATH1721 and MATH1722 there is a general description of a polynomial function:
f (x ) = a0 + a1 x 1 + a2 x 2 + . . . + an−1 x n−1 + an x n
Q: What do the superscripts on the x ’s mean?
A: Powers of the variable x .
Q: Why is x a variable (as opposed to a fixed number or constant)?
A: It appears in the brackets after f so the output variable f is a function of the input
variable x .
Q: What do the subscripts on the a’s mean?
A: They are just labels to distinguish one arbitrary number or constant from another.
Finally, notice how useful summation notation is for this sequence of added terms:
n
X
ai x i
i=0
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
18 / 29
Reading maths: summation
The mathematician Carl Gauss amazed his teacher when he could do the following sum
at the age of 8.
n=100
X
n
=
1 + 2 + 3 + · · · + 98 + 99 + 100
=
5050
n=1
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
19 / 29
Reading mathematics: drilling down
Be prepared to “dig” into maths writing:
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
20 / 29
Reading mathematics: drilling down
Be prepared to “dig” into maths writing:
Example: (MATH1001) What is the span of {(1, 1, 0), (0, 0, 2)}?
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
20 / 29
Reading mathematics: drilling down
Be prepared to “dig” into maths writing:
Example: (MATH1001) What is the span of {(1, 1, 0), (0, 0, 2)}?
Quite lot of technical information is packed into these few words!
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
20 / 29
Reading mathematics: drilling down
Be prepared to “dig” into maths writing:
Example: (MATH1001) What is the span of {(1, 1, 0), (0, 0, 2)}?
Quite lot of technical information is packed into these few words! Just because it’s a
short question, doesn’t mean it’s going to be easy.
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
20 / 29
Reading mathematics: drilling down
Be prepared to “dig” into maths writing:
Example: (MATH1001) What is the span of {(1, 1, 0), (0, 0, 2)}?
Quite lot of technical information is packed into these few words! Just because it’s a
short question, doesn’t mean it’s going to be easy.
To get into this problem, we need to do a couple of things:
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
20 / 29
Reading mathematics: drilling down
Be prepared to “dig” into maths writing:
Example: (MATH1001) What is the span of {(1, 1, 0), (0, 0, 2)}?
Quite lot of technical information is packed into these few words! Just because it’s a
short question, doesn’t mean it’s going to be easy.
To get into this problem, we need to do a couple of things:
(1) Read the notation provided:
{(1, 1, 0), (0, 0, 2)} is read as
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
20 / 29
Reading mathematics: drilling down
Be prepared to “dig” into maths writing:
Example: (MATH1001) What is the span of {(1, 1, 0), (0, 0, 2)}?
Quite lot of technical information is packed into these few words! Just because it’s a
short question, doesn’t mean it’s going to be easy.
To get into this problem, we need to do a couple of things:
(1) Read the notation provided:
{(1, 1, 0), (0, 0, 2)} is read as “the set of
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
20 / 29
Reading mathematics: drilling down
Be prepared to “dig” into maths writing:
Example: (MATH1001) What is the span of {(1, 1, 0), (0, 0, 2)}?
Quite lot of technical information is packed into these few words! Just because it’s a
short question, doesn’t mean it’s going to be easy.
To get into this problem, we need to do a couple of things:
(1) Read the notation provided:
{(1, 1, 0), (0, 0, 2)} is read as “the set of what things?
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
20 / 29
Reading mathematics: drilling down
Be prepared to “dig” into maths writing:
Example: (MATH1001) What is the span of {(1, 1, 0), (0, 0, 2)}?
Quite lot of technical information is packed into these few words! Just because it’s a
short question, doesn’t mean it’s going to be easy.
To get into this problem, we need to do a couple of things:
(1) Read the notation provided:
{(1, 1, 0), (0, 0, 2)} is read as “the set of what things? . . . vectors
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
20 / 29
Reading mathematics: drilling down
Be prepared to “dig” into maths writing:
Example: (MATH1001) What is the span of {(1, 1, 0), (0, 0, 2)}?
Quite lot of technical information is packed into these few words! Just because it’s a
short question, doesn’t mean it’s going to be easy.
To get into this problem, we need to do a couple of things:
(1) Read the notation provided:
{(1, 1, 0), (0, 0, 2)} is read as “the set of what things? . . . vectors with elements (1, 1, 0)
and (0, 0, 2).
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
20 / 29
Reading mathematics: drilling down
Be prepared to “dig” into maths writing:
Example: (MATH1001) What is the span of {(1, 1, 0), (0, 0, 2)}?
Quite lot of technical information is packed into these few words! Just because it’s a
short question, doesn’t mean it’s going to be easy.
To get into this problem, we need to do a couple of things:
(1) Read the notation provided:
{(1, 1, 0), (0, 0, 2)} is read as “the set of what things? . . . vectors with elements (1, 1, 0)
and (0, 0, 2).
(2) know the definition of “span”.
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
20 / 29
Reading mathematics: drilling down
Tips for tracking down definitions quickly:
Contents pages of unit readers.
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
21 / 29
Reading mathematics: drilling down
Tips for tracking down definitions quickly:
Contents pages of unit readers.
Indexes of texbooks.
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
21 / 29
Reading mathematics: drilling down
Tips for tracking down definitions quickly:
Contents pages of unit readers.
Indexes of texbooks.
Post-it notes at the edges of your written lecture notes.
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
21 / 29
Reading mathematics: drilling down
Tips for tracking down definitions quickly:
Contents pages of unit readers.
Indexes of texbooks.
Post-it notes at the edges of your written lecture notes.
A neat trick for electronic copies of unit readers is to use the search function:
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
21 / 29
Reading mathematics: drilling down
Now we have some notation to read:
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
22 / 29
Reading mathematics: drilling down
Now we have some notation to read:
A ={v
v1 , v2 , . . . , vk }
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
22 / 29
Reading mathematics: drilling down
Now we have some notation to read:
A ={v
v1 , v2 , . . . , vk }
This reads as
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
22 / 29
Reading mathematics: drilling down
Now we have some notation to read:
A ={v
v1 , v2 , . . . , vk }
This reads as “A is the name of
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
22 / 29
Reading mathematics: drilling down
Now we have some notation to read:
A ={v
v1 , v2 , . . . , vk }
This reads as “A is the name of the set of . . .
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
22 / 29
Reading mathematics: drilling down
Now we have some notation to read:
A ={v
v1 , v2 , . . . , vk }
This reads as “A is the name of the set of . . . vectors (since v is in boldface)
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
22 / 29
Reading mathematics: drilling down
Now we have some notation to read:
A ={v
v1 , v2 , . . . , vk }
This reads as “A is the name of the set of . . . vectors (since v is in boldface)
v1 , v2 , . . . , vk (ie. k of them).
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
22 / 29
Reading mathematics: drilling down
span(A) ={α1v1 + α2v2 + . . . + αk vk |αi ∈ R, 1 ≤ i ≤ k}
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
23 / 29
Reading mathematics: drilling down
span(A) ={α1v1 + α2v2 + . . . + αk vk |αi ∈ R, 1 ≤ i ≤ k}
This reads as
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
23 / 29
Reading mathematics: drilling down
span(A) ={α1v1 + α2v2 + . . . + αk vk |αi ∈ R, 1 ≤ i ≤ k}
This reads as “the span of set A is
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
23 / 29
Reading mathematics: drilling down
span(A) ={α1v1 + α2v2 + . . . + αk vk |αi ∈ R, 1 ≤ i ≤ k}
This reads as “the span of set A is the set of . . .
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
23 / 29
Reading mathematics: drilling down
span(A) ={α1v1 + α2v2 + . . . + αk vk |αi ∈ R, 1 ≤ i ≤ k}
This reads as “the span of set A is the set of . . .
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
23 / 29
Reading mathematics: drilling down
span(A) ={α1v1 + α2v2 + . . . + αk vk |αi ∈ R, 1 ≤ i ≤ k}
This reads as “the span of set A is the set of . . . vectors (since a linear combination of
vectors is a vector)
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
23 / 29
Reading mathematics: drilling down
span(A) ={α1v1 + α2v2 + . . . + αk vk |αi ∈ R, 1 ≤ i ≤ k}
This reads as “the span of set A is the set of . . . vectors (since a linear combination of
vectors is a vector) such that
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
23 / 29
Reading mathematics: drilling down
span(A) ={α1v1 + α2v2 + . . . + αk vk |αi ∈ R, 1 ≤ i ≤ k}
This reads as “the span of set A is the set of . . . vectors (since a linear combination of
vectors is a vector) such that each of the k numbers (αi ) is a real number.”
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
23 / 29
Reading mathematics: drilling down
span(A) ={α1v1 + α2v2 + . . . + αk vk |αi ∈ R, 1 ≤ i ≤ k}
This reads as “the span of set A is the set of . . . vectors (since a linear combination of
vectors is a vector) such that each of the k numbers (αi ) is a real number.”
Luckily, the definition includes a written explanation!
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
23 / 29
Reading mathematics: drilling down
“Drilling down” is a great method for improving your problem solving skills but don’t
worry if it leads you to a point where you can’t go on.
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
24 / 29
Reading mathematics: drilling down
“Drilling down” is a great method for improving your problem solving skills but don’t
worry if it leads you to a point where you can’t go on.
This means you have homed in on a key issue that needs sorting out rather than being
stuck at the start of the question.
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
24 / 29
Reading mathematics: drilling down
“Drilling down” is a great method for improving your problem solving skills but don’t
worry if it leads you to a point where you can’t go on.
This means you have homed in on a key issue that needs sorting out rather than being
stuck at the start of the question.
In this case, “span”, “linear combination”, etc are difficult concepts that take time to
master.
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
24 / 29
Appendix: Sets of numbers: Natural, Whole and Integers
The Natural (or Counting) Numbers:
((mα+hs)Smart
How
Workshop
to read
Semester
maths
N = {1, 2, 3, 4, . . . }
2, 2016)
Contents
Prev
Next
25 / 29
Appendix: Sets of numbers: Natural, Whole and Integers
The Natural (or Counting) Numbers:
The Whole Numbers:
N = {1, 2, 3, 4, . . . }
W = {0, 1, 2, 3, 4, . . . }
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
25 / 29
Appendix: Sets of numbers: Natural, Whole and Integers
The Natural (or Counting) Numbers:
The Whole Numbers:
The Integers:
N = {1, 2, 3, 4, . . . }
W = {0, 1, 2, 3, 4, . . . }
Z = {. . . , −2, −1, 0, 1, 2, . . . }
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
25 / 29
Appendix: Sets of numbers: Natural, Whole and Integers
The Natural (or Counting) Numbers:
The Whole Numbers:
The Integers:
N = {1, 2, 3, 4, . . . }
W = {0, 1, 2, 3, 4, . . . }
Z = {. . . , −2, −1, 0, 1, 2, . . . }
We can see that
N ⊂ W ⊂ Z.
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
25 / 29
Appendix: Sets of numbers: Rational Numbers
A rational number is a number which can be expressed as a quotient (fraction) of two
integers.
e.g.
5
,
7
3
,
8
−6
,
1
8
,
−2
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
etc
Contents
Prev
Next
26 / 29
Appendix: Sets of numbers: Rational Numbers
A rational number is a number which can be expressed as a quotient (fraction) of two
integers.
e.g.
5
,
7
3
,
8
−6
,
1
8
,
−2
etc
We denote the set of rational numbers by
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Q.
Contents
Prev
Next
26 / 29
Appendix: Sets of numbers: Rational Numbers
A rational number is a number which can be expressed as a quotient (fraction) of two
integers.
e.g.
5
,
7
3
,
8
−6
,
1
8
,
−2
etc
We denote the set of rational numbers by
Is it true that
Q.
N ⊂ W ⊂ Z ⊂ Q?
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
26 / 29
Appendix: Sets of numbers: Rational Numbers
A rational number is a number which can be expressed as a quotient (fraction) of two
integers.
e.g.
5
,
7
3
,
8
−6
,
1
8
,
−2
etc
We denote the set of rational numbers by
Is it true that
Q.
N ⊂ W ⊂ Z ⊂ Q? Yes.
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
26 / 29
Appendix: Sets of numbers: Rational Numbers
A rational number is a number which can be expressed as a quotient (fraction) of two
integers.
e.g.
5
,
7
3
,
8
−6
,
1
8
,
−2
etc
We denote the set of rational numbers by
Is it true that
Q.
N ⊂ W ⊂ Z ⊂ Q? Yes.
This is because every integer n can be written as
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
n
.
1
Prev
Next
26 / 29
Appendix: Sets of numbers: Rational Numbers
A rational number is a number which can be expressed as a quotient (fraction) of two
integers.
e.g.
5
,
7
3
,
8
−6
,
1
8
,
−2
etc
We denote the set of rational numbers by
Is it true that
Q.
N ⊂ W ⊂ Z ⊂ Q? Yes.
This is because every integer n can be written as
n
.
1
In decimal terms, rational numbers are numbers whose decimal expansion either
terminates or follows a recurring pattern:
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
26 / 29
Appendix: Sets of numbers: Rational Numbers
A rational number is a number which can be expressed as a quotient (fraction) of two
integers.
e.g.
5
,
7
3
,
8
−6
,
1
8
,
−2
etc
We denote the set of rational numbers by
Is it true that
Q.
N ⊂ W ⊂ Z ⊂ Q? Yes.
This is because every integer n can be written as
n
.
1
In decimal terms, rational numbers are numbers whose decimal expansion either
terminates or follows a recurring pattern:
22
5
is rational because
((mα+hs)Smart
How
Workshop
to read
Semester
maths
22
5
= 4.4
2, 2016)
Contents
Prev
Next
26 / 29
Appendix: Sets of numbers: Rational Numbers
A rational number is a number which can be expressed as a quotient (fraction) of two
integers.
e.g.
5
,
7
3
,
8
−6
,
1
8
,
−2
etc
We denote the set of rational numbers by
Is it true that
Q.
N ⊂ W ⊂ Z ⊂ Q? Yes.
This is because every integer n can be written as
n
.
1
In decimal terms, rational numbers are numbers whose decimal expansion either
terminates or follows a recurring pattern:
22
5
22
7
is rational because
is rational because
22
7
22
5
= 4.4
= 3.142857142857142857...
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
26 / 29
Appendix: Sets of numbers: Rational Numbers
A rational number is a number which can be expressed as a quotient (fraction) of two
integers.
e.g.
5
,
7
3
,
8
−6
,
1
8
,
−2
etc
We denote the set of rational numbers by
Is it true that
Q.
N ⊂ W ⊂ Z ⊂ Q? Yes.
This is because every integer n can be written as
n
.
1
In decimal terms, rational numbers are numbers whose decimal expansion either
terminates or follows a recurring pattern:
22
5
22
7
is rational because
is rational because
22
7
22
5
= 4.4
= 3.142857142857142857...
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
26 / 29
Appendix: Sets of numbers: Rational Numbers
A rational number is a number which can be expressed as a quotient (fraction) of two
integers.
e.g.
5
,
7
3
,
8
−6
,
1
8
,
−2
etc
We denote the set of rational numbers by
Is it true that
Q.
N ⊂ W ⊂ Z ⊂ Q? Yes.
This is because every integer n can be written as
n
.
1
In decimal terms, rational numbers are numbers whose decimal expansion either
terminates or follows a recurring pattern:
22
5
22
7
is rational because
is rational because
22
7
22
5
= 4.4
= 3.142857142857142857... = 3.142857
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
26 / 29
Appendix: Sets of numbers: Irrational Numbers
A number which is not rational is called an irrational number. These are numbers which
can not be written as ba where a and b are integers.
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
27 / 29
Appendix: Sets of numbers: Irrational Numbers
A number which is not rational is called an irrational number. These are numbers which
can not be written as ba where a and b are integers.
For a number to be irrational, it must have an infinite decimal expansion which has no
recurring pattern.
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
27 / 29
Appendix: Sets of numbers: Irrational Numbers
A number which is not rational is called an irrational number. These are numbers which
can not be written as ba where a and b are integers.
For a number to be irrational, it must have an infinite decimal expansion which has no
recurring pattern.
The number π is irrational, as its decimal expansion is:
3.141592653589793238463 . . .
There is no recurring pattern here.
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
27 / 29
Appendix: Sets of numbers: Irrational Numbers
A number which is not rational is called an irrational number. These are numbers which
can not be written as ba where a and b are integers.
For a number to be irrational, it must have an infinite decimal expansion which has no
recurring pattern.
The number π is irrational, as its decimal expansion is:
3.141592653589793238463 . . .
There is no recurring pattern here.
Other irrational numbers include
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
27 / 29
Appendix: Sets of numbers: Irrational Numbers
A number which is not rational is called an irrational number. These are numbers which
can not be written as ba where a and b are integers.
For a number to be irrational, it must have an infinite decimal expansion which has no
recurring pattern.
The number π is irrational, as its decimal expansion is:
3.141592653589793238463 . . .
There is no recurring pattern here.
√ √ √
2, 3, 5, . . . (ie. the square root of any number
Other irrational numbers include
that isn’t a perfect square).
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
27 / 29
Appendix: Sets of numbers: Irrational Numbers
A number which is not rational is called an irrational number. These are numbers which
can not be written as ba where a and b are integers.
For a number to be irrational, it must have an infinite decimal expansion which has no
recurring pattern.
The number π is irrational, as its decimal expansion is:
3.141592653589793238463 . . .
There is no recurring pattern here.
√ √ √
2, 3, 5, . . . (ie. the square root of any number
Other irrational numbers include
that isn’t a perfect square).
The exponential number, e is also irrational:
e = 2.71828182845 . . .
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
27 / 29
Appendix: Sets of numbers: Irrational Numbers
A number which is not rational is called an irrational number. These are numbers which
can not be written as ba where a and b are integers.
For a number to be irrational, it must have an infinite decimal expansion which has no
recurring pattern.
The number π is irrational, as its decimal expansion is:
3.141592653589793238463 . . .
There is no recurring pattern here.
√ √ √
2, 3, 5, . . . (ie. the square root of any number
Other irrational numbers include
that isn’t a perfect square).
The exponential number, e is also irrational:
e = 2.71828182845 . . .
We denote the set of irrational numbers by
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Q.
Contents
Prev
Next
27 / 29
Appendix: Sets of numbers: Real Numbers
If we take the union of the set of rational numbers with the set of irrational numbers we
get the set of real numbers. We denote this set by R.
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
28 / 29
Appendix: Sets of numbers: Real Numbers
If we take the union of the set of rational numbers with the set of irrational numbers we
get the set of real numbers. We denote this set by R.
Real numbers are all on the real number line.
-5
-4
-3
-2
-1
0
1
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
2
3
Contents
4
Prev
5
Next
28 / 29
Using STUDYSmarter Resources
This resource was developed for UWA students by the STUDYSmarter team for the
numeracy program. When using our resources, please retain them in their original form
with both the STUDYSmarter heading and the UWA crest.
((mα+hs)Smart
How
Workshop
to read
Semester
maths
2, 2016)
Contents
Prev
Next
29 / 29