* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Projectile Motion - RHIG
Electrical resistance and conductance wikipedia , lookup
Weightlessness wikipedia , lookup
Speed of gravity wikipedia , lookup
Classical mechanics wikipedia , lookup
Lorentz force wikipedia , lookup
Newton's theorem of revolving orbits wikipedia , lookup
Partial differential equation wikipedia , lookup
History of fluid mechanics wikipedia , lookup
Work (physics) wikipedia , lookup
Two New Sciences wikipedia , lookup
Time in physics wikipedia , lookup
Aristotelian physics wikipedia , lookup
Newton's laws of motion wikipedia , lookup
Classical central-force problem wikipedia , lookup
PHY
5200 Mechanical
Phenomena
Projectile
Motion
PHY 5200
Mechanical Phenomena
Newton’s Laws of Motion
Click to editClaude
MasterA title
style
Pruneau
Physics and Astronomy Department
Wayne State University
Dec
2005.
Click
Claude
to
edit
A Pruneau
Master subtitle style
Physics and Astronomy
Wayne State University
1
Content
• Projectile Motion
–
–
–
–
Air Resistance
Linear Air Resistance
Trajectory and Range in a Linear Medium
Quadratic Air Resistance
• Charge Particle Motion
– Motion of a Charged Particle in a Uniform Field
– Complex Exponentials
– Motion in a Magnetic Field
Description of Motion with F=ma
• F=ma, as a law of Nature applies to a very wide
range of problems whose solution vary greatly
depending on the type of force involved.
• Forces can be categorized as being “fundamental” or
“effective” forces.
• Forces can also be categorized according to the
degree of difficulty inherent in solving the 2nd order
differential equation F = m a.
– Function of position only
– Function of speed, or velocity
– Separable and non-separable forces
• In this Chapter
– Separable forces which depend on position and velocity.
– Non separable forces.
Air Resistance
• Air Resistance is neglected in introductory treatment
of projectile motion.
• Air Resistance is however often non-negligible and
must be accounted for to properly describe the
trajectories of projectiles.
– While the effect of air resistance may be very small in some
cases, it can be rather important and complicated e.g.
motion of a golf ball.
• One also need a way/technique to determine whether
air resistance is important in any given situation.
Air Resistance - Basic Facts
• Air resistance is known under different names
– Drag
– Retardation Force
– Resistive Force
• Basic Facts and Characteristics
–
–
–
–
Not a fundamental force…
Friction force resulting from different atomic phenomena
Depends on the velocity relative to the embedding fluid.
Direction of the force opposite to the velocity (typically).
• True for spherical objects, a good and sufficient approximation
for many other objects.
• Not a good approximation for motion of a wing (airplane) additional force involved called “lift”.
– Here, we will only consider cases where the force is antiparallel to the velocity - no sideways force.
Air Resistance - Drag Force
•
Consider retardation force strictly antiparallel to the velocity.
!
f = ! f (v)v̂
•
Where
!
v
v̂ =
!
v
f(v) is the magnitude of the force.
•
•
Measurements reveal f(v) is
complicated - especially near the speed
of sound…
At low speed, one can write as a good
approximation:
f (v) = bv + cv 2 = flin + fquad
v̂
!
f = ! f (v)v̂
!
!
w = mg
Air Resistance - Definitions
f (v) = bv + cv 2 = flin + fquad
flin ! bv
Viscous drag
• Proportional to viscosity of the medium
and linear size of object.
fquad ! cv 2
Inertial
• Must accelerate mass of air which is in
constant collision.
• Proportional to density of the medium
and cross section of object.
For a spherical projectile (e.g. canon ball, baseball, drop of rain):
b = !D
c = ! D2
Where D is the diameter of the sphere
βand γ depend on the nature of the medium
At STP in air:
! = 1.6 " 10 #4 Nis / m 2
$ = 0.25Nis / m 4
Air Resistance - Linear or Quadratic
• Often, either of the linear or quadratic terms can be neglected.
• To determine whether this happens in a specific problem, consider
fquad
flin
=
cv
!D
=
v = 1.6 # 10 3 ms2
bv
"
(
2
)
$ ! 1: linear case
&
Dv %
&" 1: quadratic case
'
• Example: Baseball and Liquid Drops
• A baseball has a diameter of D = 7 cm, and travel at speed of order v=5 m/s.
fquad
flin
! 600
!
f = !cv 2 v̂
• A drop of rain has D = 1 mm and v=0.6 m/s
fquad
flin
Neither term can be neglected.
!1
• Millikan Oil Drop Experiments, D=1.5 mm and v=5x10-5 m/s.
fquad
flin
! 10
"7
!
!
f = !bv
Air Resistance - Reynolds Number
• The linear term drag is proportional to the viscosity, η
• The quadratic term is related to the density of the
fluid, ρ.
• One finds
fquad
flin
!R!
Dv"
#
Reynolds Number
Case 1: Linear Air Resistance
•
•
Consider the motion of projectile for which
one can neglect the quadratic drag term.
From the 2nd law of Newton:
x
y
v̂
!
!
f = !bv
!
!
w = mg
!"" !
!
!
mr = F = mg ! bv
•
•
Independent of position, thus:
!"
!
!
mv = mg ! bv
Furthermore, it is separable in coordinates (x,y,z).
m!vx = !bvx
m!vy = mg ! bvy
•
A 1st order differential equation
Two separate differential equations
Uncoupled.
By contrast, for f(v)~v2, one gets coupled y vs x motion
!
!
f = !cv 2 v̂ = !c vx2 + vy2 v
m!vx = !c vx2 + vy2 vx
m!vy = mg ! c vx2 + vy2 vy
Case 1: Linear Air Resistance - Horizontal Motion
•
•
•
Consider an object moving horizontally in a resistive linear medium.
Assume vx = vx0, x = 0 at t = 0.
!
!
Assume the only relevant force is the drag force.
•
Obviously, the object will slow down
•
Define (for convenience): k =
•
Thus, one must solve:
•
Clearly:
•
Which can be re-written:
f = !bv
v!x = !
b
vx
m
b
m
dv
v!x = x = !kvx
dt
dvx
= !kdt
vx
vx (t) = vx 0 e!t /"
dvx
! vx = "k ! dt
with
! =1/ k = m /b
Velocity exhibits exponential decay
ln vx = !kt + C
Case 1: Linear Air Resistance - Horizontal Motion
(cont’d)
• Position vs Time, integrate
t
dx
"0 dt ! dt ! = x(t) # x(0)
• One gets
t
x(t) = x(0) + $ vx 0 e! t " /# dt "
0
= 0 + %& !vx 0# e
(
! t " /#
'( o
x(t) = x! 1 " e"t /#
x! $ vx 0#
t
(
x(t) = x! 1 " e"t /#
)
x! $ vx 0#
)
vx (t) = vx 0 e!t /"
Vertical Motion with Linear Drag
•
Consider motion of an object thrown
vertically downward and subject to gravity
and linear air resistance.
!
!
f = !bv
x
y
v̂
!
!
w = mg
m!vy = mg ! bvy
•
Gravity accelerates the object down, the
speed increases until the point when the
retardation force becomes equal in
magnitude to gravity. One then has
terminal speed.
0 = mg ! bvy
mg
vter = vy (a = 0) =
b
Note dependence on mass and linear drag coefficient b.
Implies terminal speed is different for different objects.
Equation of vertical motion for linear drag
•
The equation of vertical motion is determined by
m!vy = mg ! bvy
•
Given the definition of the terminal speed,
•
One can write instead
mg
vter =
b
(
m!vy = !b vy ! vterm
•
Or in terms of differentials
(
)
)
mdvy = !b vy ! vterm dt
•
Separate variables
dvy
vy ! vterm
•
Change variable:
bdt
=!
m
u = vy ! vterm
du = dvy
du
bdt
=!
= !kdt
u
m
where
k=
b
m
Equation of vertical motion for linear drag (cont’d)
•
So we have …
du
bdt
=!
= !kdt
u
m
•
Integrate
du
! u = "k ! dt
•
Or…
u = Ae! kt
•
Remember
u = vy ! vterm
•
So, we get
vy ! vter = Ae!t /"
•
•
Now apply initial conditions: when t = 0, vy = vy0
This implies
v ! v = Ae!0 /" = A
•
The velocity as a function of time is thus given by
y0
ln u = !kt + C
! =1/ k = m /b
with
ter
(
)
vy = vter + vy0 ! vter e!t /"
(
vy = vy0 e!t /" + vter 1 ! e!t /"
)
Equation of vertical motion for linear drag (cont’d)
(
vy = vy0 e!t /" + vter 1 ! e!t /"
•
We found
•
At t=0, one has
•
Whereas for
•
As the simplest case, consider vy0=0,
I.e. dropping an object from rest.
)
vy = vy0
t!"
vy = vy0
(
vy = vter 1 ! e!t /"
)
time percent of
t/tau vter
0
0.0
1
63.2
2
86.5
3
95.0
4
98.2
5
99.3
Equation of vertical motion for linear drag (cont’d)
•
•
Vertical position vs time obtained by integration!
Given
•
The integration yields
(
)
vy = vter + vy0 ! vter e!t /"
(
)
y = vter t ! " vy0 ! vter e!t /" + C
•
Assuming an initial position y=y0, and initial velocity vy = vy0.
One gets
(
)
y0 = !" vy0 ! vter + C
(
C = y0 + ! vy0 " vter
)
x
•
The position is thus given by
(
y
)(
y = y0 + vter t + ! vy0 " vter 1 " e"t /!
)
!
!
f = !bv
v̂
!
!
w = mg
Equation of vertical motion for linear drag (cont’d)
•
•
!
!
f = !bv
Note that it may be convenient to reverse the
direction of the y-axis.
Assuming the object is initially thrown upward, the
position may thus be written
(
)(
y = y0 ! vter t + " vy0 + vter 1 ! e
!t / "
)
v̂
y
x
!
!
w = mg
Equation of motion for linear drag (cont’d)
•
Combine horizontal and vertical equations to get the trajectory of a projectile.
(
)
x(t) = vx 0! 1 " e"t /!
y(t) = y0 ! vter t + " vy0 + vter 1 ! e!t /"
•
(
)(
)
To obtain an equation of the form y=y(x), solve the 1st equation for t, and
substitute in the second equation.
y(t) = y0 +
vy0 + vter
vx 0
#
x &
x + vter! ln % 1 "
vx 0! ('
$
Example: Projectile Motion
5
50
2
200
490
b
vx0*tau
(vy0+vter)*tau
0.1
100
34500
vter*tau
24500
y (m)
m
tau
vx0
vy0
vter
Linear friction
No friction
x (m)
Horizontal Range
• In the absence of friction (vacuum), one has
x(t) = vxot
y(t) = vyot !
0.98 2
2
t
• The range in vacuum is therefore
Rvac =
2vxo vyo
g
• For a system with linear drag, one has
0=
vy0 + vter
vx 0
#
R &
R + vter! ln % 1 "
vx 0! ('
$
A transcendental equation - cannot be solved analytically
Horizontal Range (cont’d)
R ! vxo!
•
If the the retardation force is very weak…
•
So, consider a Taylor expansion of the logarithm in 0 =
•
Let
•
We get ln(1 ! " ) = ! " + 12 " 2 + 13 " 3 + ...
•
Neglect orders beyond
!=
R
vxo"
•
We now get
•
This leads to
(
0=
vx 0
)
!3
2
3
) R
1# R &
1# R & ,
R ! vter" +
+ %
(' + 3 %$ v " (' .
v
"
2
v
"
$
+* x 0
.x0
x0
vy0 + vter
vx 0
R=0
R=
vy0 + vter
2vxo vyo
g
R ! Rvac "
!
2
R2
3vxo"
$
2
4 vyo '
2
Rvac
= Rvac & 1 "
3vxo#
3 vter )(
%
#
R &
R + vter! ln % 1 "
vx 0! ('
$
Quadratic Air Resistance
•
For macroscopic projectiles, it is usually a better approximation to
consider the drag force is quadratic
!
2!
f = !cv v
•
Newton’s Law is thus
•
Although this is a first order equation, it is NOT separable in x,y,z
components of the velocity.
!"
!
2!
mv = mg ! cv v
Horizontal Motion with Quadratic Drag
•
•
•
We have to solve
m
dv
= !cv 2
dt
Separation of v and t variables permits
independent integration on both sides of
the equality…
dv
= !cdt
v2
Rearrange
m
Integration
dv!
m " 2 = #c " dt !
v!
vo
0
Yields
) 1 1,
# 1&
m % ! ( = m + ! . ! ct
* v0 v $ v" ' v0
v
t
where
v = vo
at t = 0.
v
•
•
Solving for v
v(t) =
•
Note: for t=τ,
v(! ) =
v0
v0
=
1 + cv0t / m 1 + t / !
v0
= v0 / 2
1+! /!
with
!=
m
cvo
Horizontal Motion with Quadratic Drag (cont’d)
•
Horizontal position vs time obtained by integration …
t
x(t) = x + " v(t ! )dt !
0
= v0# ln(1 + t / # )
v(t) =
•
Never stops increasing
•
By contrast to the “linear” case.
(
x(t) = vx 0! 1 " e"t /!
•
Which saturates…
•
Why? ! ?
v0
1+ t /!
)
x(t) = v0! ln(1 + t / ! )
•
The retardation force becomes
quite weak as soon as v<1.
•
In realistic treatment, one must include both the linear and quadratic terms.
Vertical Motion with Quadratic Drag
dv
= mg ! cv 2
dt
•
Measuring the vertical position, y, down. m
•
Terminal velocity achieved for vter =
•
For the baseball of our earlier example, this yields ~ 35 m/s or 80 miles/hour
•
2
Rewrite in terms of the terminal velocity dv = g " 1 ! v %
$#
dt
v 2 '&
mg
c
ter
dv
= gdt
v2
1! 2
vter
•
Solve by separation of variables
•
Integration yields
! v $
vter
arctanh #
=t
g
" vter &%
Solve for v
! gt $
v = vter tanh # &
" vter %
•
•
Integrate to find
2
vter ) '
! gt $ *
(
y=
ln cosh
g
)
(
#" v &% ,
ter +
Quadratic Draw with V/H motion
• Equation of motion
!
!
m""
r = mg ! cv 2 v̂
!
!
= mg ! cvv
• With y vertically upward
m!vx = !c vx2 + vy2 vx
m!vy = !mg ! c vx2 + vy2 vy
Motion of a Charge in Uniform Magnetic Field
•
•
•
•
•
Another “simple” application of Newton’s 2nd law…
Motion of a charged particle, q, in a uniform magnetic field, B, pointing
in the z-direction.
Z
The force is
!
! !
F = qv ! B
!
B
The equation of motion
!"
! !
mv = qv ! B
!
v
The 2nd reduces to a first order Eq.
x
•
Components of velocity and field
(
!
v = v x , v y , vz
!
B = ( 0, 0, B )
)
(
!
v = vy B, !vx B, 0
)
y
Motion of a Charge in Uniform Magnetic Field (cont’d)
• Three components of the Eq of motion
m!vx = qBvy
m!vy = !qBvx
m!vz = 0
• Define
( v , v ) ! transverse velocity
x
!=
• Rewrite
vz = constant
y
qB
m
v!x = ! vy
v!y = "! vx
Cyclotron frequency
Coupled Equations
Solution in the complex plane …
Complex Plane
y
(imaginary
part)
Representation of the velocity vector
! = vx + ivy
vy
O
vx
i = !1
x (real part)
Why and How using complex numbers for this?
• Velocity
! = vx + ivy
• Acceleration
!! = v!x + iv!y
• Remember Eqs of motion
v!x = ! vy
v!y = "! vx
• We can write
• Or
(
!! = v!x + iv!y = " vy # i" vx = #i" vx + ivy
!! = "i#!
)
Why and How using … (cont’d)
• Equation of motion
!! = "i#!
• Solution
! = Ae"i# t
• Verify by substitution
d!
= "i# Ae"i# t = "i#!
dt
Complex Exponentials
•
Taylor Expansion of Exponential
2
3
z
z
ez = 1 + z + + + !
2! 3!
•
•
The series converges for any value of z (real or complex, large or
small).
It satisfies
(
) (
d
Aekz = k Aekz
dz
•
)
And is indeed a general solution for df (z) = kf (z)
dz
•
So we were justified in assuming η is a solution of the Eqs of motion.
Complex Exponentials (cont’d)
The exponential of a purely imaginary number is
2
3
4
i
!
i
!
i
!
(
)
(
)
(
)
e! = 1 + i! +
+
+
+!
2!
3!
4!
where θ is a real number
Separation of the real and imaginary parts - since i2=-1, i3=-I
# !2 !4
& #
&
!3
e = %1 "
+
" !( + i %! " + !(
2!
4!
3!
$
' $
'
!
cos!
sin !
We get Euler’s Formula
i!
e = cos! + i sin !
Complex Exponentials (cont’d)
• Euler’s Formula implies eiθ lies on a unit circle.
i!
e = cos! + i sin !
y
cos!
ei!
1
O
sin !
!
x
cos 2 ! + sin 2 ! = 1
Complex Exponentials (cont’d)
• A complex number expressed in the polar form
i!
A = ae = a cos! + ia sin !
where a and θ are real numbers
a cos!
y
A = ae
a
!
i!
a 2 cos 2 ! + a 2 sin 2 ! = a 2
a sin !
Amplitude
Phase
O
x
! = Ae
"i# t
!i" t
! = Ae
"i# t
= ae
Angular Frequency
i ($ " # t )
Solution for a charge in uniform B field
z(t) = zo + vzot
•
vz constant implies
•
The motion in the x-y plane best represented by introduction of
complex number.
! = x + iy
Greek letter “xi”
•
The derivative of ξ
•
Integration of η
!! = x! + i!y = vx + ivy = "
! = # "dt = # Ae$i% t dt
iA #i" t
! = e + constant
"
x + iy = Ce!i" t + ( X+iY)
Solution for a charge in uniform B field (cont’d)
x + iy = Ce!i" t + ( X+iY)
Redefine the z-axis so it passes through (X,Y)
x + iy = Ce!i" t
y
which for t = 0, implies
xo + iyo
C = xo + iyo
Motion frequency
!=
qB
m
xo2 + yo2
O
x
x + iy
!t
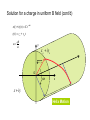
Solution for a charge in uniform B field (cont’d)
x(t) + iy(t) = Ce!i" t
z(t) = zo + vzot
!=
qB
m
y
xo + iyo
xo2 + yo2
O
!t
x
x + iy
Helix Motion