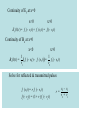Download ReviewWavesO

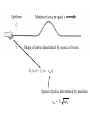
Review of Waves
Properties of electromagnetic waves in vacuum:
Waves propagate through vacuum (no medium is required like
sound waves)
All frequencies have the same propagation speed, c in vacuum.
Electric and magnetic fields are oriented transverse to the direction
of propagation. (transverse waves)
Waves carry both energy and momentum.
E and B fields in waves and Right Hand Rule:
f+ solution
f- solution
Wave propagates in E x B direction
Special Case Sinusoidal Waves
Ey (x, t) = f+ (x - vem t) = E0 cos [k(x - vem t)]
E y (x, t)
E0
Wavenumber and
wavelength
k = 2p / l
l = 2p / k
- E0
These two contain
the same
information
Special Case Sinusoidal Waves
Ey (x, t) = f+ (x - vem t) = E0 cos [k(x - vem t)]
E y (x, t)
2p = kvemT
E0
Introduce
w = 2p / T
f = 1/T
- E0
Different ways of saying the same thing:
w / k = vem
fl = vem
Polarizations
We picked this combination
of fields: Ey - Bz
Could have picked this
combination of fields: Ez - By
These are called plane polarized. Fields lie in plane
Which of the following are valid EM waves?
Ex (z, t) = E0 cos[k(z - vem t)]
1.
A. Yes
B. No
2.
A.Yes
B. No
E0
By (z, t) =
cos[k(z - vem t)]
vem
Ey (y, t) = E0 cos [k(y - vem t)]
E0
Bz (y, t) =
cos[k(y - vem t)]
vem
3.
A.Yes
B. No
Ex (y,t) = E0 cos[k(y + vem t)]
Bz (y,t) =
4.
E0
cos[k(y + vem t)]
vem
What direction is this wave propagating
in?
A.
B.
C.
D.
Y
Z
X
None of
above
Ex (y, z, t) = E0 cos[ky cos q + kz sin q - wt ]
w= ?
r
B= ?
z
Direction of propagation
ŷ cos q + ẑ sin q
Ex
.
q
By , Bz
Wave Vector
r
k = k (ŷ cosq + ẑ sin q)
y
Ex (y, z, t) = E0 cos[ky cos q + kz sin q - wt ]
w = kvem
Ex
By (y, z, t) = sin q
vemE
Bz (y, z, t) = - cos q x
vem
Energy Density and Intensity of EM Waves
Energy density associated with electric and magnetic fields
uE 
For a wave:
r 2
0 E
2
uB 
r 2
B
2 0
r
1 r
B 
E   0 0 E
vem
Thus:
uE  u B
Units: J/m3
Energy density in electric and magnetic fields are equal for a wave in
vacuum.
We now want to expand the picture in the following way:
EM waves propagate in 3D not just 1D as we have considered.
- Diffraction - waves coming from a finite source spread out.
EM waves propagate through material and are modified.
- Dispersion - waves are slowed down by media, different
frequency waves travel with different speeds
- Reflection - waves encounter boundaries between media.
Some energy is reflected.
- Refraction - wave trajectories are bent when crossing from
one medium to another.
EM waves can take multiple paths and arrive at the same point.
- Interference - contributions from different paths add or
cancel.
Waves emanating from a
point source
Wave crests
When can one consider waves to be
like particles following a trajectory?
Motion of crests
Direction of power flow
• Wave model: study solution of Maxwell equations.
Most complete classical description. Called physical
optics.
• Ray model: approximate propagation of light as that of
particles following specific paths or “rays”. Called
geometric optics.
• Quantum optics: Light actually comes in chunks called
photons
l
Comparable to
opening size
What is the difference?
Diffraction.
l
Much smaller
than opening
size
Diffraction
Propagation of light through dielectric media
In a dielectric the Electric field causes molecules/atoms to
become polarized.
Molecules align with field
Medium becomes “polarized”
What happens when the electric field oscillates in time?
A current is induced.
Iµ
ŽE
Žt
How is the Ampere-Maxwell Law modified?
Dielectric
For S2 there is both displacement current and real current
Real current given by
dielectric constant
I through = e0 (k - 1)
ŽE
Žt
dF e
dt
Dielectric constant
k
Iµ
Electric flux
In a dielectric material
r r
dF e
B³d
S
=
m
(e
k
)
0
0
—
Ú
dt
Bottom Line:
k
Replace
e0
by
e0 k
Dielectric constant
Static dielectric constants
To complicate matters,
dielectric constant depends
on frequency.
Dielectric function depends
on frequency
Consequences for EM Plane waves
Ey (x, t) = f+ (x - vem t) + f- (x + vem t)
Bz (x, t) =
1
( f+ (x - vemt)- f- (x + vemt))
vem
vem = 1 / m0 e0k = c / k
Propagation speed changes
in a material
Refraction
For sinusoidal waves
the following is still
true
fl = vem
Ratio of E to B changes
Reflection
w / k = vem
Index of refraction
n=
speed of light in vacuum
c
=
=
speed of light in material vem
k
For sinusoidal waves
the following is still
true
fl = vem
w / k = vem
Frequency is the same in
both media
Wavelength changes
A light wave travels through three
transparent materials of equal thickness.
Rank in order, from the largest to smallest,
the indices of refraction n1, n2, and n3.
A. n1 > n2 > n3
B. n2 > n1 > n3
C. n3 > n1 > n2
D. n3 > n2 > n1
E. n1 = n2 = n3
Example: Optical fiber
d
Fused silica: n=1.48
In vacuum
0 r 2
I
E
0
Vacuum wavelength l = 1550 nm
Wavelength in fiber l/n = 1045nm
D = 10 m
P=1mW inside fiber
I=P/A=?
E=?
Rays bounce back and forth
Reflection from surface
incident
reflected
Region 1
transmitted
Region 2
v1 = 1 / m0 e0k 1
Reflection coefficient
What if
k 1 = k 2 , v1 = v2
v2 = 1 / m0 e0k 2
r=
v2 - v1
v2 + v1
“Index matched”
Ey, Bz
How to calculate reflection
region 1
For x<0
incident
0
At x=0 fields are
continuous
region 2
reflected
x
For x>0
transmitted
Ey (x, t) = f+ (x - v1t) + f- (x + v1t)
E y (x, t) = ft (x - v2 t)
1
Bz (x, t) = ( f+ (x - v1t)- f- (x + v1t))
v1
1
Bz (x, t) =
ft (x - v2 t)
v2
v1 = 1 / m0 e0k 1
v1 = 1 / m0 e0k 1
Continuity of Ey at x=0
x<0
x>0
Ey (0, t) = f+ (- v1t) + f- (v1t) = ft (- v2 t)
Continuity of Bz at x=0
x<0
Bz (0, t) =
x>0
1
1
f
(v
t)f
(v
t)
=
ft (- v2 t)
(+ 1
1 )
v1
v2
Solve for reflected & transmitted pulses
f- (v1t) = r f+ (- v1t)
ft (- v2 t) = (1+ r ) f+ (- v1t)
r=
v2 - v1
v2 + v1
Example: what fraction of power is reflected at boundary between
glass and air?
Reflection coefficient
Air: n1=1.0003
r=
v2 - v1 n1 - n2
=
v2 + v1 n1 + n2
Glass: n2 =1.5
n1 - n2 1- 1.5
r=
=
= - 0.2
n1 + n2 1+ 1.5
I=Power/Area
0 r 2
I
E
0
I Refl   2 I Inc
I Refl  0.04I Inc
ratio of reflected to incident
electric field amplitude
ratio of reflected to incident
intensity
Suppose the wave was incident on the
boundary from the glass side
incident
reflected
Region 1
v1 = 1 / m0 e0k 1
n1=1.5
transmitted
Region 2
v2 = 1 / m0 e0k 2
n2=1.0
v2 - v1 n1 - n2
What is reflection coefficient? r = v + v = n + n
2
1
1
2
incident
reflected
Region 1
v1 = 1 / m0 e0k 1
n1=1.5
What is reflection coefficient?
A. =0
B.  =.2
C.  =-.2
D.  =5
transmitted
Region 2
v2 = 1 / m0 e0k 2
n2=1.0
v2 - v1 n1 - n2
r=
=
v2 + v1 n1 + n2
Region 2 has higher velocity
r=
v2 - v1 n1 - n2
=
>0
v2 + v1 n1 + n2
Region 2 has lower velocity
v2 - v1 n1 - n2
r=
=
<0
v2 + v1 n1 + n2
What if
k 2 , n2 Æ •
r=
n1 - n2
Æ- 1
n1 + n2
Same as for reflection
from a conductor
Interference in 1 Dimension
incident
Incident and reflected fields
add (superposition)
reflected
incident reflected
Ey (x, t) = E0 cos [k(x - v1t)]+ r E0 cos [k(x + v1t)]
Incident and reflected waves will interfere, changing the peak
electric field at different points
1.5
Case #1: no reflection =0.
No interference,
1
E (x,t)
0.5
y
0
E plotted versus x for
several values of t
-0.5
-1
-1.5
-10
-8
-6
-4
-2
0
x
1
E plotted versus t for a
single value of x.
y
E (x,t)
0.5
0
Same peak value
independent of x
-0.5
Traveling wave
-1
0
2
4
6
t
8
10
3
Case #2: total reflection = -1.
Anti-nodes
2
E plotted versus x for
several values of t
0
y
E (x,t)
1
-1
-2
nodes
-3
-10
-8
-6
-4
-2
0
x
3
How far apart are the nodes?
Anti-nodes?
What is peak E?
2
Case #3: total reflection = +1.
y
E (x,t)
1
0
E plotted versus x for
several values of t
-1
-2
-3
-10
-8
-6
-4
x
-2
0
Emax Emin
2
Case #4: partial reflection = -0.5
1.5
1
y
E (x,t)
0.5
E plotted versus x for
several values of t
0
-0.5
-1
-1.5
-2
-10
-8
-6
-4
-2
x
0
How far apart are the minima?
The Maxima?
What is peak E?
When reflection is not total there are still local maxima and minima.
Emax 1+ r
=
Emin 1- r
= VSWR
Voltage Standing Wave Ratio
Pronounced “vizwarr”
Half Wavelength Window
Eliminates Reflection
incident
incident
reflected
Region 1
n1
Region 2
transmitted
Region 1’
n2
D
D = ml 2 / 2 = ml Vac / (2n2 )
When dielectric #2 is an integer number
of half-wavelengths thick, no reflection
n1
CVD diamond window
Manufactured by
elementsix
http://www.e6.com/wps/wcm/connect/E6_Content_EN/Home
Summary
1. Waves are modified by dielectric constant of medium, k.
2. All our Maxwell equations are valid provided we replace
e0 Æ e0k
3. Speed of waves is lowered. (Index of refraction - n)
speed of light in vacuum
c
n=
=
=
speed of light in material vem
k
4. Frequency of wave does not change in going from one
medium to another. Wavelength does. l = l vac / n
5. Waves are reflected at the boundary between two media.
(Reflection coefficient)
v2 - v1 n1 - n2
r=
=
v2 + v1 n1 + n2
6. Reflected waves interfere with incident waves.
Distance between interference maxima/minima l / 2
Ratio of maximum peak field to minimum peak field
(Voltage standing wave ratio)
Emax 1+ r
=
Emin 1- r
= VSWR
Solution of the Wave equation
Ž2 Ey (x, t)
Žx
2
= m0 e0
Ž2 Ey (x, t)
Žt 2
Ey (x, t) = f+ (x - vem t) + f- (x + vem t)
Where f+,- are any two functions you like,
and
v = 1/ m e
em
0 0
vem is a property of space.
vem = 2.9979¥ 10 8 m / s
f+ ,- Represent forward and backward propagating wave
(pulses). They depend on how the waves were launched
Shape of pulse determined by source of wave.
Ey (x, t) = f+ (x - vem t)
Speed of pulse determined by medium
vem = 1 / m0 e0
What is the magnetic field of the wave?
Ey (x, t) = f+ (x - vem t) + f- (x + vem t)
Bz (x, t) =
1
( f+ (x - vemt)- f- (x + vemt))
vem
Notice minus sign
Ey (V/m)
The graph at the top is the history graph
at x = 4 m of a wave traveling to the right
at a speed of 2 m/s. Which is the history
graph of this wave at x = 0 m?
What is the
frequency of this
traveling wave?
A. 0.1 Hz
B. 0.2 Hz
C. 2 Hz
D. 5 Hz
E. 10 Hz
What is the phase difference between
the crest of a wave and the adjacent
trough?
A. 0
B. π
C. π /4
D. π /2
E. 3 π /2