Download Exercise Sheet 1

MAT 182: Analysis für die Naturwissenschaften HS2016
Dr. C. Luchsinger
Exercise Sheet 1 - Solution
Exercise 1 (5 Points)
a) (1 Point)
x1,2 =
−(−5) ±
p
√
(−5)2 − 4 · 1 · 4
5 ± 25 − 16
5±3
=
=
2·1
2
2
⇒
x1 = 4 , x2 = 1
b
.
b) (1 Point) From y = ax2 +bx+c the x coordinate can be computed using xs = − 2a
This yields: xs = 2.5 and ys = −2.25
c) (2 Points) We use the approach y = mx + q. We have the unknowns m and q and
need two equations.
The point (3/ − 2) lies on the line and the parabola. So we have −2 = 3m + q.
(1 Point)
In addition the line and the parabola touch each other at (3/ − 2). Consequently the equation x2 − 5x + 4 = mx + q has one solution only. Rearranged
to x2 − (5 + m)x + (4 − q) = 0 and solved for x we have:
p
5 + m ± (5 + m)2 − 4 · 1 · (4 − q)
x1,2 =
2·1
There is one solution for x if the term under the root disappears. This is our
second equation. Directly
x1 = x2 =
5+m
=3
2
one gets
−2 = 3m + q so q = −5.
The tangent equation is y = x − 5.
m=1
(1 Point)
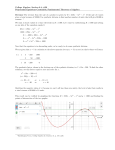
d) (1 Point) The Graph.
y
y = x2 − 5x + 4
y =x−5
x
1
Exercise 2 (6 Points)
(a) (2 Points) The domain of the equation is D = R\{3}
x2
x−3
2
9
= 1 + x−3
x =x−3+9
2
x −x−6=0
(x − 3)(x + 2) = 0
This leads to the solutions x1 = 3 and x2
| ·(x − 3)
| −x − 6
| factor
(1 Point)
|
= −2 . Thus L = {−2}. (1 Point)
(b) (2 Points) By substituting 3x := z the equation translates to
z 2 − 10z + 9 = 0
By factoring (z−9)(z−1) = 0 one gets z1 = 1 and z2 = 9.
From z1 = 1 we have: 3x = 1 ⇒ x1 = 0
From z2 = 9 we have: 3x = 9 = 32 ⇒ x2 = 2
(1 Point)
(c) (2 Points) Guessing leads to the first solution x1 = −1. Polynomial division
yields
(x3 − 4x2 + x + 6) : (x + 1) = x2 − 5x + 6
(1 Point)
−(x3 + x2 )
− 5x2 + x + 6
−(−5x2 − 5x)
6x + 6
−(6x + 6)
0
Furthermore x2 − 5x + 6 = (x − 2)(x − 3). Solving the equation (x + 1)(x −
2)(x − 3) = 0 is simple.
We have L = {−1, 2, 3}.
(1 Point)
Exercise 3 (4 Points)
(a) (2 Points)
2x + y + z = 10
x − 2y − z = −3
2x − y + 2z = 8
2
(1)
(2)
(3)
We eliminate z by (1) & (2) und (2) & (3)
2x + y + z = 10
x − 2y − z = −3
⇒ 3x − y = 7
(1)
(2)
(4)
2x − 4y − 2z = −6
2x − y + 2z = 8
(2) · 2
(3)
⇒
(5)
4x − 5y = 2
(1 Point)
x and y can now be determined by (4) & (5)
15x − 5y = 35
4x − 5y = 2
⇒ 11x = 33 ⇒
(4) · 5
(5)
x=3
From (4) y = 2 follows and from (1) we immediately see z = 2.
(1 Point)
(b) (2 Points)
2x + y + z = 10
x − 2y − z = −3
5x + z = 17
(1)
(2)
(3)
The variable z can be eliminated directly:
(1) + (2) ⇒
(2) + (3) ⇒
3x − y = 7
(4)
6x − 2y = 14
(5)
(1 Point)
Apparantly equation (5) is a multiple of (4). We plug x = t into (4). This leads
to y = 3t − 7. z is determined by equation (3). z = 17 − 5x = 17 − 5t.
The solution as an equation of a straight line is

  
 
t
0
1
(1 Point)
~r =  3t − 7  = −7 + t ·  3 
17 − 5t
17
−5
Exercise 4 (5 Points)
a) (2 Points)
2
2
2
2
y 0 = f 0 (x) = 2xe−x + x2 (−2x)e−x = 2xe−x − 2x3 e−x = 2(x − x3 )e−x
2
2
2
y 00 = f 00 (x) = 2(1 − 3x2 )e−x + 2(x − x3 ) · (−2x)e−x = 2(1 − 5x2 + 2x4 )e−x
3
(1 Point)
2
(1 Point)
b) (2 Points) Maxima and Minima: f(x) is a continuous function without any
boundary points (f (±∞) = 0). So we focus on y 0 = 0.
(1 Point)
y 0 = 0 ⇔ x1 = 0 and x2,3 = ±1
00
Since f (0) = 2 > 0 we have a Minimum. f(0)=0
Since f 00 (±1) < 0 we have Maxima at x = ±1. Furthermore: f (±1) = e−1 .
(1 Point)
c) (1 Point) The function is symmetric to the y-axis because f (x) = f (−x). It is an
even function.
4