Download Series and Parallel Resonance 5-19-11

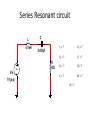
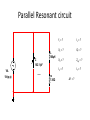
Series and Parallel Resonance
Series Resonant circuit
L
4.7mH
C
0.001µF
R
47Ω
Vin
1V (p-p)
fr = ?
VC = ?
XC = ?
VL = ?
XL = ?
Q=?
IT = ?
∆f = ?
Θ=?
Find fr
• fr =
6.28
1
2𝜋 𝐿𝐶
1
=
1
6.28
4.7×10−12
=
4.7×10−3
1
1.362×10−5
0.001×10−6
=
= 73.412kHz
Find reactances
• XL = 2πfL = (6.28)(73.142X103)(4.7X10-6) =
2.168kΩ
•
1
1
XC =
=
2𝜋𝑓𝐶
6.28 73.142×103 0.001×10−6
1
= 2.168kΩ
−4
4.613×10
=
Since XC and XL are equal, along with being 180° out
of phase, the net reactance is zero which makes the
total impedance equal to the resistor ∴ ZT = R
Find total current and voltages
• IT =
𝑉𝑖𝑛
𝑍𝑇
=
𝑉𝑖𝑛
𝑅
=
0.3535
=
47
7.521mA
Since this is a series circuit, the current found for
the total will also be the current flowing through
the reactive components.
• VC = (XC)(IT) = (2.168kΩ)(7.521mA) = 16.306V
• VL = (XL)(IT) = (2.168kΩ)(7.521mA) = 16.306V
As you can see, the resonant circuit appears to
amplify the voltages.
Find the Q of the circuit
• Q=
𝑋𝐿
𝑟𝑠
 Since there is no value given for a
resistance of the coil, we have to use the only
resistance in the circuit to find this value
𝑋𝐿 2.168𝑘𝛺
∴Q= =
= 46.128
𝑅
47𝛺
Solve for Bandwidth and Cutoff
frequencies
𝑓𝑟
𝑄
73.142𝑘𝐻𝑧
46.128
• ∆𝑓 = 𝑓2 − 𝑓1 = =
= 1.592kHz
This means the frequency will vary ±796Hz
∆𝑓
. The entire range is also known as
2
Bandwidth.
• f2 =
∆𝑓
fr + = 73.412kHz + 796Hz = 74.208kHz
2
∆𝑓
fr - = 73.412kHz - 796Hz = 72.616kHz
2
• f1 =
• θ = 0° since XL and XC are canceling, which means
at resonance the circuit is purely resistive.
Parallel Resonant circuit
C
162.11pF
L
100µH
VA
10v(p-p)
50%
rs
7.85Ω
fr = ?
IL = ?
XL = ?
Q=?
XC = ?
Zeq = ?
IC = ?
IT = ?
∆f = ?
Solve for fr
• fr =
6.28
1
2𝜋 𝐿𝐶
1
=
1
6.28
1.621×10−14
100×10−6
=
1
799×10−9
162.11×10−12
= 1.25MHz
=
Find the reactances
• XL = 2πfL = (6.28)(1.25X106)(100X10-6) =
785.394Ω
•
1
1
XC =
=
2𝜋𝑓𝐶
6.28 1.25×106 162.11×10−12
1
= 785.417Ω
−3
1.273×10
=
Since this is a parallel circuit, we presume the
applied voltage will be across each reactive
component.
Find branch currents and the
equivalent impedance
•
•
•
𝑉𝐴
10
IC = =
= 12.732mA
𝑋𝑐 785.417
𝑉𝐴
10
IL = =
= 12.732mA
𝑋𝐿 785.398
𝑋𝐿 785.398
Q= =
= 100.051 ≅
𝑟𝑠
7.85
100
• Zeq = QXL = (100.051)(785.398) = 78.58kΩ 
Since this is the only way we are going to get
the total impedance, we now need to use it to
find the total current.
Find total current
• IT =
𝑉𝐴
𝑍𝑒𝑞
=
10
78.58𝑘𝛺
= 127.259µA
Again, we can see the magnification of the
current due to resonance.
Solve for Bandwidth and Cutoff
frequencies
• ∆𝑓 = 𝑓2 − 𝑓1 =
𝑓𝑟
𝑄
=
1.25𝑀𝐻𝑧
100.051
= 12.494kHz
This means the frequency will vary
±6.247kHz
• f2 =
• f1 =
∆𝑓
2
∆𝑓
fr + = 1.25MHz + 6.247kHz = 1.256MHz
2
∆𝑓
fr - = 1.25MKz – 6.247kHz = 1.243MHz
2