Download Chapter 13, example problems:

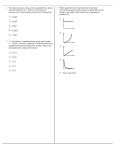
Chapter 13, example problems:
x (cm)
(13.04) Reading Fig. 13-30 (reproduced on the right): 10.0
(a) Frequency f = 1/ T = 1/ (16s) = 0.0625 Hz.
(since the figure shows that T/2 is 8 s.)
0
(b) The amplitude is 10 cm. (Don’t just say 10!)
(c) The period T is 16 s.
(d) The angular frequency ω is:
2π/ T = 2π/ (16 s) = (π/8) s−1 = 0.3927 s−1.
-10.0
Better yet, the unit should be given as rad/s,
since 2π is actually 2π rad.
5.0
10.0
15.0
(13.14) Object undergoing SHM. T = 1.200 s, and A = 0.600 m.
At t = 0, object is at x = 0. At t = 0.480 s, x = ?
In general, x = A cos (ωt + φ). But since at t = 0, object is at x = 0, we must take
φ = ± π/2, and obtain x = ±A sin (ωt). (The sign can not be decided since we do
not know whether the objected started by moving to the right or left.) Thus at
t = 0.480 s, we have x = ± 0.600 m sin ((2π/1.200 s)×(0.480 s)) = ± 0.353 m.
That is, the object is 0.353 m away from the equilibrium position.
(13.28) 5.20 kg box attached to an ideal horizontal spring with k = 375 N/m. Inside the
box, a stone with m = 3.44 kg. Oscillating with A = 7.50 cm. When at
maximum speed, the stone is plucked vertically out of the box without touching
the box.
(a) T new = 2π / ω max = 2π /√k/m new = 2π / (375 N/m / 5.20 kg)1/2 = 0.740 s.
(b) The plucking does not exert any horizontal force to the motion of the box. The
empty box will still have the maximum velocity of the original motion, which is
vmax = ω A = √k/m A = (375 N/m / 8.64 kg)1/2 ×7.50 cm = 49.4 cm/s. But its
angular frequency has changed to √k/m new = (375 N/m / 5.20 kg)1/2 = 8.492 1/s.
Hence its new amplitude is Anew = vmax /ω new = 49.4 cm/s / 8.492 1/s = 5.817 cm.
(c) The new period is shorter, since it is now a lighter mass moving under the
influence of the same spring. (The same spring force produces a larger
acceleration on the lighter mass at any given displacement. So the frequency
should be higher, and the period shorter.)
(13.44) A simple pendulum on Mars: On earth its period is 1.60 s. On Mars where
g = 3.71 m/s2, the new period is:
T Mars = 2π /√g Mars /l = (√g Earth / √g Mars) ×(2π /√g Earth /l )
= (√9.80 / 3.71) ×1.60 s = 2.60 s.
That is, the period is longer on Mars, because lower gravitational acceleration on
Mars makes the swinging motion slower.
(13.52) 1.80 kg monkey wrench pivoted 0.250 m from its center of mass. Allowed to
swing as a physical pendulum. Period of small-angle oscillation = 0.940 s.
(a) Moment of inertia of the wrench:
t (s)
I = mgl / ω 2 = 1.80 kg × 9.80 m/s2 × 0.250 m /(2π / 0.940 s)2 = 0.0987 kg m2,
(where use has been made that ω = √mgl/I for a physical pendulum at smallangle oscillation, because the gravitational torque is τ = − mgl sinθ, so for smallangle oscillations for which sinθ can be approximated by θ, the effective torque
constant K is mgl. Thus ω = √K/I becomes √mgl/I. )
(b) Initial displacement = θ (t = 0) = 0.400 rad. Want dθ /d t at θ = 0, i.e., ( dθ /d t ) max.
We use energy conservation: (1/2) K θ max2 = (1/2) I ( dθ /d t ) max2 [which is the
angular analog of (1/2) k x max2 = (1/2) m vmax2 . The left hand side is at both
extremes of the motion, where the velocity is zero, whereas the right hand side is
at the center of the motion, where the displacement is zero.]
Hence ( dθ /d t ) max = θ max (K / I)1/2 = ωθ max = (2π / 0.940 s) × 0.400 rad
= 2.674 rad/s.
(13.68) Before the small block slips, the frequency
of the oscillation is: f = (1/2π) √k/(m + M) .
μs
Looking at the small block alone, the only
horizontal force acting on it is the static
m
k
frictional force, the maximum value of
M
which is: μsN = μsmg, (because the upward
normal force N acing on the small block
by the large block below it should cancel
the downward weight of the small block, mg.)
frictionless
For slip to not occur to the small block, this
maximum frictional force must be equal to its
mass m times its maximum acceleration, or Aω2.
That is: μsmg = mAω2 = mA [k/(m + M)], giving A = μs(m+M)g/k.
(13.70) Rocket accelerating upward at 4.00 m/s2 from launchpad on earth. A small 1.50
kg ball hangs from the ceiling inside the rocket by a light 1.10-m wire. The ball
is displaced by 8.50° from vertical and released.
(i) Inside the rocket, the effective g is 9.80 m/s2 + 4.00 m/s2 = 13.80 m/s2. Why?
Because when the ball is in its equilibrium position below the hanging point of
the ceiling, and T is the tension in the wire, which pulls the ball upward, then the
Newton’s second law gives T – mg = m × 4.00 m/s2, giving T = m × 13.80 m/s2.
Thus the period of the oscillation is:
2π √L/geff = 2π √1.10 m/13.80 m/s2 = 1.77 s.
Remarks: (a) Einstein’s “equivalence principle” precisely refers to this situation:
In a “frame” which is accelerating upward with an acceleration a, any mass m
behaves as if it has received an additional downward force equal to its mass m
times a. Adding it to the downward weight mg of the mass m if it is near the
surface of the earth, we find that the total force acting on the mass is m (g + a), as
if g has been changed to (g + a). (b) Both tension and period are denoted by T.
To avoid confusing we have not used T to denote the period here, so T stands for
tension only here. In another problem in this chapter we will use T to denote
period.
(ii) The amplitude of the oscillation is still 1.10 m × (8.50° × π radians / 180°) =
0.163 m, independent of the acceleration of the rocket.
(13.80) A 40.0 N force stretches a vertical spring 0.250 m.
(a) Find m suspended from it to get a period of 1.00 s.
Force constant of the spring k = 40.0 N / 0.250 m = 160 N/m.
T = 2π (m / k)1/2 = 1.00 s. ⇒ m = k (T / 2π )2 = 160 N/m (1.00 s / 2π )2 = 4.05 kg.
(c) A = 0.050 m, T = 1.00 s. Find x(t) and direction of motion at t = 0.35 s after the
mass m has passed the equilibrium position, moving downward.
We take downward as positive for x, measured from the new equilibrium
position (which is 0.248 m below the lower end of the unstretched spring), then
x(t) = A sin (ωt) = A sin (2π f t) = A sin (2π t / T )
= 0.050 m × sin (2π × 0.35 s / 1.00 s) = 0.0405 m.
[Note that the argument of the sine function is in radians as revealed by the
2π factor. The formula ω = 2π f = 2π / T gives the angular frequency ω in
radians per second.] As for the direction of motion at this t, we notice that
0.35 s / 1.00 s = 0.35 < 0.5 but > 0.25. Thus the argument of the sine function
has exceeded π / 2 but is still less than π. Thus the sine function has reached its
first maximum and is now coming down. It means that the mass m is now
moving toward the origin (i.e., the equilibrium position). You can also answer
this question by computing the velocity, but it will take more time.
(d) Find the force F acting on the mass when it is 0.030 m below the equilibrium
position moving upward. We use F = − k x = − 160 N/m × 0.03 m = − 4.80 N.
The negative sign shows that this force is pointing upward, not because the
motional velocity is pointing upward (given in the problem), but rather because
x is positive. (The restoring force in a simple harmonic oscillator is always
trying to bring the mass back to the origin.)
[Note that you can also use F = m a and a = − ω 2 x to do this problem, and the
same answer will be obtained.
(13.90) Model the leg of a T. rex. as two uniform rods, each 1.55 m long, joined rigidly
end to end. The lower rod has mass M and the upper rod has mass 2M. The
composite opject is pivoted about the top of the upper rod. Compute the
oscillation period of this object for small amplitude oscillation. Compare results
with that of Example 13.10.
We need to first find the moment of inertia and center-of-mass location of this
object.
P
The total moment of inertia about P :
2
2
I = [(1/12)(2M) × L + (2M) × (L/2) ] +
θ
[(1/12)(M) × L2 + (M) × (3L/2)2]
= (2/3)ML2 + (14/6)ML2 = 3ML2
Let the center of mass of this composite object
be located at a distance d from the pivot point P
along the rod. Then an upward force of 3Mg at this
point can support the whole object. Thus the
2Mg
Mg
counterclockwise torque by this force at this point
about P can balance the two clockwise torques about
P, one by the weight 2Mg at (L/2) from P, and one by
weight Mg at (3L/2) from P. That is,
(3Mg) × d sin θ = (2Mg) × (L/2) sin θ + (Mg) × (3L/2) sin θ
giving d = (5/6) L. [This answer is independent of θ, so one could let θ = 90°.]
We are now ready to compute the oscillation period of this composite object:
T = 2π [I / (3M)gd ]1/2 = 2π (L2 / gd )1/2 = 2π [1.55 m / 9.80 m/s2 × (5/6)]1/2 = 2.74 s.
Example 13.10 found a period of 2.90 s by assuming that the object is a uniform
rod of the same length 2L = 3.10 m. Clearly, by shifting the mass distribution
toward the pivot point, the period becomes shorter. This is clearly right, since if
the whole mass is concentrated at the lower end (farthest from the pivot point),
we would get T = 2π [2L / g ]1/2 = 3.53 s ! Note that in all three cases, the
answer does not depend on the total mass, only its distribution.
(13.96)
0.100m
0.100 m
0.200 m
P1
m
0.200 m
P2
Both springs are stretched from their natural length 0.200 m to 0.300 m so their
free ends can be attached to the points P1 and P2.
(a) If k1 = 2.00 N/m and k2 = 6.00 N/m, find the new equilibrium position of the
block of mass m.
Let the new equilibrium position be a distance x to the right of the original
position. Then the (left) spring 1 is stretched by 0.100 m + x, and the (right)
spring 2 is stretched by 0.100 m – x. The force pulling the block to the left by
the spring 1 is therefore F1 = k1 × (0.100 m + x), and the force pulling the block
to the right by the spring 2 is therefore F2 = k2 × (0.100 m − x). These two force
should cancel each other for the new equilibrium position. Hence we obtain the
equation: 2.00 N/m × (0.100 m + x) = 6.00 N/m × (0.100 m − x). Recombining
terms, we obtain 0.600 N – 0.200 N = (2.00 N/m + 6.00 N/m) × x. Solving for x
and we obtain x = 0.05 m. Thus the new equilibrium position of the block is
0.05 m to the right of its initial position.
(b) Find the period of oscillation of the block if it is slightly displaced from this new
equilibrium position and released.
Let the block be displaced by a distance y to the right of this new equilibrium
position. Then the spring 1 is stretch by a total distance (0.100 m + x + y), and
the spring 2 is stretched by a total distance (0.100 m –x – y). The force pulling
the block to the left by the spring 1 is therefore F1 = k1 × (0.100 m + x + y), and
the force pulling the block to the right by the spring 2 is therefore F2 = k2 ×
(0.100 m − x – y). These two forces no longer cancel, and the net force to the
right (i.e., in the direction of the displacement y) is F2 – F1 = − (k1 + k2 ) × y,
showing that the effective force constant for this oscillatory motion is (k1 + k2 ) .
Thus the period of this oscillatory motion is:
T = (2π) √ m / ( k1 + k2 ) = (2π) √0.100 kg / 8.00 N/m = 0.7025 s.