Download CURRENT, RESISTANCE, AND ELECTROMOTIVE FORCE

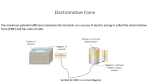
CURRENT, RESISTANCE, AND
ELECTROMOTIVE FORCE
Chapter 4
CURRENT AND CURRENT DENSITY
• Current is the amount of charge
flowing through a specified area, per
unit time.
• The SI unit of current is the ampere,
equal to one coulomb per second (1
A = 1 C/s).
CURRENT AND CURRENT DENSITY
• The current I through an area A
depends on the concentration n and
charge q of the charge carriers, as
well as on the magnitude of their
drift velocity 𝑣𝑑 .
• The current density is current per
unit cross-sectional area.
CURRENT AND CURRENT DENSITY
• Current is conventionally described
in terms of a flow of positive charge,
even when the actual charge carriers
are negative or of both signs.
𝑑𝑄
𝐼=
= 𝑛 𝑞 𝑣𝑑 𝐴
𝑑𝑡
𝐽 = 𝑛𝑞 𝑣𝑑
EXAMPLE
An 18-gauge copper wire (the size usually
used for lamp cords) has a nominal
diameter of 1.02 mm. This wire carries a
constant current of 1.67 A to a 200-watt
lamp. The density of free electrons is 8.5 x
1028 electrons per cubic meter. Find the
magnitudes of (a) the current density and
(b) the drift velocity.
EXAMPLE
(a) Magnitude of current density
𝐼
𝐽=
𝐴
Cross-sectional area of the wire
2
𝜋𝑑
𝐴 = 𝜋𝑟 2 =
4
𝜋 1.02𝑥10−3 𝑚 2
=
4
= 8.17𝑥10−7 𝑚2
EXAMPLE
𝐼
𝐽=
𝐴
1.67 𝐴
=
8.17 𝑥 10−7 𝑚2
= 2.04 𝑥 106 𝐴 𝑚2
EXAMPLE
(b)
𝐽 = 𝑛 𝑞 𝑣𝑑
𝐽
𝑣𝑑 =
𝑛𝑞
2.04 𝑥 106 𝐴 𝑚2
=
8.5 𝑥 1028 𝑚−3 −1.60 𝑥 10−19 𝐶
= 1.5 𝑥 10−4 𝑚 𝑠
= 0.15 𝑚𝑚/𝑠
RESISTIVITY
• The resistivity ρ of a material is the
ratio of the magnitudes of electric
field and current density.
• Good conductors have small
resistivity; good insulators have large
resistivity.
RESISTIVITY
• Ohm’s law, obeyed approximately by many
materials, states that ρ is a constant independent
of the value of E.
• Resistivity usually increases with temperature; for
small temperature changes this variation is
represented approximately by the following
equations, where α is the temperature coefficient
of resistivity.
𝐸
𝜌=
𝐽
𝜌 𝑇 = 𝜌0 1 + 𝛼 𝑇 − 𝑇0
RESISTORS
• For materials obeying Ohm’s law, the
potential difference V across a
particular sample of material is
proportional to the current I through
the material.
• The ratio V/I = R is the resistance of
the sample.
RESISTORS
• The SI unit of resistance is the ohm (1 Ω =
1 V/A).
• The resistance of a cylindrical conductor
is related to its resistivity ρ, length L, and
cross-sectional area A.
𝑉 = 𝐼𝑅
𝜌𝐿
𝑅=
𝐴
EXAMPLE
The 18-gauge copper wire in the previous
example has a diameter of 1.02 mm and a
cross-sectional area of 8.20 x 10-7 m2. It
carries a current of 1.67 A. Find (a) the
electric-field magnitude in the wire; (b) the
potential difference between two points in
the wire 50.0 m apart; (c) the resistance of
a 50.0-m length of this wire.
EXAMPLE
(a) Resistivity ρ of copper = 1.72 x 10-8 Ω·m
𝐸
𝜌=
𝐽
𝐸 = 𝜌𝐽
𝜌𝐼
=
𝐴
1.72 𝑥 10−8 Ω ∙ 𝑚 1.67 𝐴
=
8.20 𝑥 10−7 𝑚2
= 0.0350 𝑉 𝑚
EXAMPLE
(b) The potential difference is given by
𝑉 = 𝐸𝐿
= 0.0350 𝑉 𝑚 50.0 𝑚
= 1.75 𝑉
(c) The resistance is
𝑉
𝑅=
𝐼
1.75 𝑉
=
1.67 𝐴
= 1.05 Ω
CIRCUITS AND EMF
• A complete circuit has a continuous
current-carrying path.
• A complete circuit carrying a steady
current must contain a source of
electromotive force (emf) ε.
CIRCUITS AND EMF
• The SI unit of electromotive force is
the volt (1 V).
• An ideal source of emf maintains a
constant potential difference,
independent of current through the
device, but every real source of emf
has some internal resistance r.
CIRCUITS AND EMF
• The terminal potential difference Vab
then depends on current.
𝑉𝑎𝑏 = 𝜀 − 𝐼𝑟
(source with internal resistance)
EXAMPLE
The figure shows a source (a battery) with an
emf ε of 12 V and an internal resistance r of 2 Ω.
(For comparison, the internal resistance of a
commercial 12-V lead storage battery is only a
few thousandths of an ohm). The wires to the
left of a and to the right of the ammeter A are
not connected to anything. Determine the
readings of the idealized voltmeter V and the
idealized ammeter A.
EXAMPLE
EXAMPLE
• There is no current because there is
no complete circuit.
• Hence the ammeter A reads I = 0.
𝑉𝑎𝑏 = 𝜀 − 𝐼𝑟
𝑉𝑎𝑏 = 𝜀
= 12 𝑉
ENERGY AND POWER IN CIRCUITS
• A circuit element with a potential difference
𝑉𝑎 − 𝑉𝑏 = 𝑉𝑎𝑏 and a current I puts energy into
a circuit if the current direction is from lower
to higher potential in the device, and it takes
energy out of the circuit if the current is
opposite.
• The power P (rate of energy transfer) is equal
to the product of the potential difference and
the current.
ENERGY AND POWER IN CIRCUITS
• A resistor always takes electrical energy
out of a circuit.
𝑃 = 𝑉𝑎𝑏 𝐼
(general circuit element)
2
𝑉𝑎𝑏
2
𝑃 = 𝑉𝑎𝑏 𝐼 = 𝐼 𝑅 =
𝑅
(power into a resistor)
EXAMPLE
For the given figure, find the rate of energy
conversion (chemical to electrical) and the rate
of dissipation of energy in the battery and the
net power output of the battery.
EXAMPLE
• The rate of conversion in the battery is
𝜀𝐼 = 12 𝑉 2 𝐴 = 24 𝑊
• The rate of dissipation of energy in the
battery is
2
2
𝐼 𝑟 = 2𝐴 2Ω =8𝑊
• The electrical power output is:
2
𝜀𝐼 − 𝐼 𝑟 = 16 𝑊
CONDUCTION IN METALS
• The microscopic basis of conduction in metals
is the motion of electrons that move freely
through the metallic crystal, bumping into ion
cores in the crystal.
• In a crude classical model of this motion, the
resistivity of the material can be related to the
electron mass, charge, speed of random
motion, density, and mean free time between
collisions.
DIRECT-CURRENT CIRCUITS
Chapter 4
RESISTORS IN SERIES AND PARALLEL
• When several resistors R1, R2, R3, …,
are connected in series, the
equivalent resistance Req is the sum
of the individual resistances.
• The same current flows through all
the resistors in a series connection.
RESISTORS IN SERIES AND PARALLEL
• When several resistors are connected in parallel, the
reciprocal of the equivalent resistance Req is the sum of the
reciprocals of the individual resistances.
• All resistors in a parallel connection have the same potential
difference between their terminals.
𝑅𝒆𝒒 = 𝑅1 + 𝑅2 + 𝑅3 + ⋯
(resistors in series)
1
𝑅𝑒𝑞
=
1
𝑅1
+
1
𝑅2
+
1
𝑅3
+⋯
(resistors in parallel)
KIRCHHOFF’S RULES
• Kirchhoff’s junction rule is based on
conservation of charge.
• It states that the algebraic sum of the
current into any junction must be
zero.
KIRCHHOFF’S RULES
• Kirchhoff’s loop rule is based on
conservation of energy and the
conservative nature of electrostatic
fields.
• It states that the algebraic sum of
potential difference around any loop
must be zero.
KIRCHHOFF’S RULES
• Careful use of consistent sign rules is
essential in applying Kirchhoff’s
rules.
𝐼 = 0 (junction rule)
𝑉 = 0 (loop rule)
ELECTRICAL MEASURING
INSTRUMENTS
• In a d’Arsonal galvanometer, the
deflection is proportional to the
current in the coil.
• For a larger current range, a shunt
resistor is added, so some of the
current bypasses the meter coil. Such
an instrument is called an ammeter.
ELECTRICAL MEASURING
INSTRUMENTS
• If the coil and any additional series
resistance included obey Ohm’s law,
the meter can also be calibrated to
read potential difference or voltage.
• The instrument is then called a
voltmeter.
ELECTRICAL MEASURING
INSTRUMENTS
• A good ammeter has very low
resistance; a good voltmeter has very
high resistance.
R-C CIRCUITS
• When a capacitor is charged by a
battery in series with a resistor, the
current and capacitor charge are not
constant.
• The charge approaches its final value
asymptotically and the current
approaches zero asymptotically.
R-C CIRCUITS
• After a time 𝜏 = 𝑅𝐶, the charge has
approached within 1/𝑒 of its final
value.
• This time is called the time constant
or relaxation time of the circuit.
R-C CIRCUITS
• When the capacitor discharges, the
charge and current are given as
functions of time.
• The time constant is the same for
charging and discharging.
R-C CIRCUITS
• Capacitor charging:
𝑞 = 𝐶𝜀 1 − 𝑒 −𝑡/𝑅𝐶
𝑡
−
𝑒 𝑅𝐶 )
= 𝑄𝑓 (1 −
𝑑𝑞 𝜀 −𝑡
𝑖=
= 𝑒
𝑑𝑡 𝑅
−𝑡 𝑅𝐶
= 𝐼0 𝑒
𝑅𝐶
R-C CIRCUITS
• Capacitors discharging:
−𝑡 𝑅𝐶
𝑞 = 𝑄0 𝑒
𝑑𝑞
𝑄0 −𝑡
𝑖=
=−
𝑒
𝑑𝑡
𝑅𝐶
−𝑡 𝑅𝐶
= 𝐼0 𝑒
𝑅𝐶
HOUSEHOLD WIRING
• In household wiring systems, the various
electrical devices are connected in
parallel across the power line, which
consists of a pair of conductors, one
“hot” and the other “neutral”.
• An additional “ground” wire is included
for safety.
HOUSEHOLD WIRING
• The maximum permissible current in
a circuit is determined by the size of
the wires and the maximum
temperature they can tolerate.
• Protection against excessive current
and the resulting fire hazard is
provided by fuses or circuit breakers.