* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download CURRENT, RESISTANCE, AND ELECTROMOTIVE FORCE
Giant magnetoresistance wikipedia , lookup
Negative resistance wikipedia , lookup
Electric charge wikipedia , lookup
Lumped element model wikipedia , lookup
Operational amplifier wikipedia , lookup
Integrated circuit wikipedia , lookup
Power MOSFET wikipedia , lookup
Nanofluidic circuitry wikipedia , lookup
Superconductivity wikipedia , lookup
Nanogenerator wikipedia , lookup
Surge protector wikipedia , lookup
Flexible electronics wikipedia , lookup
Thermal runaway wikipedia , lookup
Resistive opto-isolator wikipedia , lookup
Opto-isolator wikipedia , lookup
Electromigration wikipedia , lookup
Galvanometer wikipedia , lookup
Rectiverter wikipedia , lookup
Current source wikipedia , lookup
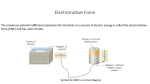
CURRENT, RESISTANCE, AND ELECTROMOTIVE FORCE Chapter 4 CURRENT AND CURRENT DENSITY • Current is the amount of charge flowing through a specified area, per unit time. • The SI unit of current is the ampere, equal to one coulomb per second (1 A = 1 C/s). CURRENT AND CURRENT DENSITY • The current I through an area A depends on the concentration n and charge q of the charge carriers, as well as on the magnitude of their drift velocity 𝑣𝑑 . • The current density is current per unit cross-sectional area. CURRENT AND CURRENT DENSITY • Current is conventionally described in terms of a flow of positive charge, even when the actual charge carriers are negative or of both signs. 𝑑𝑄 𝐼= = 𝑛 𝑞 𝑣𝑑 𝐴 𝑑𝑡 𝐽 = 𝑛𝑞 𝑣𝑑 EXAMPLE An 18-gauge copper wire (the size usually used for lamp cords) has a nominal diameter of 1.02 mm. This wire carries a constant current of 1.67 A to a 200-watt lamp. The density of free electrons is 8.5 x 1028 electrons per cubic meter. Find the magnitudes of (a) the current density and (b) the drift velocity. EXAMPLE (a) Magnitude of current density 𝐼 𝐽= 𝐴 Cross-sectional area of the wire 2 𝜋𝑑 𝐴 = 𝜋𝑟 2 = 4 𝜋 1.02𝑥10−3 𝑚 2 = 4 = 8.17𝑥10−7 𝑚2 EXAMPLE 𝐼 𝐽= 𝐴 1.67 𝐴 = 8.17 𝑥 10−7 𝑚2 = 2.04 𝑥 106 𝐴 𝑚2 EXAMPLE (b) 𝐽 = 𝑛 𝑞 𝑣𝑑 𝐽 𝑣𝑑 = 𝑛𝑞 2.04 𝑥 106 𝐴 𝑚2 = 8.5 𝑥 1028 𝑚−3 −1.60 𝑥 10−19 𝐶 = 1.5 𝑥 10−4 𝑚 𝑠 = 0.15 𝑚𝑚/𝑠 RESISTIVITY • The resistivity ρ of a material is the ratio of the magnitudes of electric field and current density. • Good conductors have small resistivity; good insulators have large resistivity. RESISTIVITY • Ohm’s law, obeyed approximately by many materials, states that ρ is a constant independent of the value of E. • Resistivity usually increases with temperature; for small temperature changes this variation is represented approximately by the following equations, where α is the temperature coefficient of resistivity. 𝐸 𝜌= 𝐽 𝜌 𝑇 = 𝜌0 1 + 𝛼 𝑇 − 𝑇0 RESISTORS • For materials obeying Ohm’s law, the potential difference V across a particular sample of material is proportional to the current I through the material. • The ratio V/I = R is the resistance of the sample. RESISTORS • The SI unit of resistance is the ohm (1 Ω = 1 V/A). • The resistance of a cylindrical conductor is related to its resistivity ρ, length L, and cross-sectional area A. 𝑉 = 𝐼𝑅 𝜌𝐿 𝑅= 𝐴 EXAMPLE The 18-gauge copper wire in the previous example has a diameter of 1.02 mm and a cross-sectional area of 8.20 x 10-7 m2. It carries a current of 1.67 A. Find (a) the electric-field magnitude in the wire; (b) the potential difference between two points in the wire 50.0 m apart; (c) the resistance of a 50.0-m length of this wire. EXAMPLE (a) Resistivity ρ of copper = 1.72 x 10-8 Ω·m 𝐸 𝜌= 𝐽 𝐸 = 𝜌𝐽 𝜌𝐼 = 𝐴 1.72 𝑥 10−8 Ω ∙ 𝑚 1.67 𝐴 = 8.20 𝑥 10−7 𝑚2 = 0.0350 𝑉 𝑚 EXAMPLE (b) The potential difference is given by 𝑉 = 𝐸𝐿 = 0.0350 𝑉 𝑚 50.0 𝑚 = 1.75 𝑉 (c) The resistance is 𝑉 𝑅= 𝐼 1.75 𝑉 = 1.67 𝐴 = 1.05 Ω CIRCUITS AND EMF • A complete circuit has a continuous current-carrying path. • A complete circuit carrying a steady current must contain a source of electromotive force (emf) ε. CIRCUITS AND EMF • The SI unit of electromotive force is the volt (1 V). • An ideal source of emf maintains a constant potential difference, independent of current through the device, but every real source of emf has some internal resistance r. CIRCUITS AND EMF • The terminal potential difference Vab then depends on current. 𝑉𝑎𝑏 = 𝜀 − 𝐼𝑟 (source with internal resistance) EXAMPLE The figure shows a source (a battery) with an emf ε of 12 V and an internal resistance r of 2 Ω. (For comparison, the internal resistance of a commercial 12-V lead storage battery is only a few thousandths of an ohm). The wires to the left of a and to the right of the ammeter A are not connected to anything. Determine the readings of the idealized voltmeter V and the idealized ammeter A. EXAMPLE EXAMPLE • There is no current because there is no complete circuit. • Hence the ammeter A reads I = 0. 𝑉𝑎𝑏 = 𝜀 − 𝐼𝑟 𝑉𝑎𝑏 = 𝜀 = 12 𝑉 ENERGY AND POWER IN CIRCUITS • A circuit element with a potential difference 𝑉𝑎 − 𝑉𝑏 = 𝑉𝑎𝑏 and a current I puts energy into a circuit if the current direction is from lower to higher potential in the device, and it takes energy out of the circuit if the current is opposite. • The power P (rate of energy transfer) is equal to the product of the potential difference and the current. ENERGY AND POWER IN CIRCUITS • A resistor always takes electrical energy out of a circuit. 𝑃 = 𝑉𝑎𝑏 𝐼 (general circuit element) 2 𝑉𝑎𝑏 2 𝑃 = 𝑉𝑎𝑏 𝐼 = 𝐼 𝑅 = 𝑅 (power into a resistor) EXAMPLE For the given figure, find the rate of energy conversion (chemical to electrical) and the rate of dissipation of energy in the battery and the net power output of the battery. EXAMPLE • The rate of conversion in the battery is 𝜀𝐼 = 12 𝑉 2 𝐴 = 24 𝑊 • The rate of dissipation of energy in the battery is 2 2 𝐼 𝑟 = 2𝐴 2Ω =8𝑊 • The electrical power output is: 2 𝜀𝐼 − 𝐼 𝑟 = 16 𝑊 CONDUCTION IN METALS • The microscopic basis of conduction in metals is the motion of electrons that move freely through the metallic crystal, bumping into ion cores in the crystal. • In a crude classical model of this motion, the resistivity of the material can be related to the electron mass, charge, speed of random motion, density, and mean free time between collisions. DIRECT-CURRENT CIRCUITS Chapter 4 RESISTORS IN SERIES AND PARALLEL • When several resistors R1, R2, R3, …, are connected in series, the equivalent resistance Req is the sum of the individual resistances. • The same current flows through all the resistors in a series connection. RESISTORS IN SERIES AND PARALLEL • When several resistors are connected in parallel, the reciprocal of the equivalent resistance Req is the sum of the reciprocals of the individual resistances. • All resistors in a parallel connection have the same potential difference between their terminals. 𝑅𝒆𝒒 = 𝑅1 + 𝑅2 + 𝑅3 + ⋯ (resistors in series) 1 𝑅𝑒𝑞 = 1 𝑅1 + 1 𝑅2 + 1 𝑅3 +⋯ (resistors in parallel) KIRCHHOFF’S RULES • Kirchhoff’s junction rule is based on conservation of charge. • It states that the algebraic sum of the current into any junction must be zero. KIRCHHOFF’S RULES • Kirchhoff’s loop rule is based on conservation of energy and the conservative nature of electrostatic fields. • It states that the algebraic sum of potential difference around any loop must be zero. KIRCHHOFF’S RULES • Careful use of consistent sign rules is essential in applying Kirchhoff’s rules. 𝐼 = 0 (junction rule) 𝑉 = 0 (loop rule) ELECTRICAL MEASURING INSTRUMENTS • In a d’Arsonal galvanometer, the deflection is proportional to the current in the coil. • For a larger current range, a shunt resistor is added, so some of the current bypasses the meter coil. Such an instrument is called an ammeter. ELECTRICAL MEASURING INSTRUMENTS • If the coil and any additional series resistance included obey Ohm’s law, the meter can also be calibrated to read potential difference or voltage. • The instrument is then called a voltmeter. ELECTRICAL MEASURING INSTRUMENTS • A good ammeter has very low resistance; a good voltmeter has very high resistance. R-C CIRCUITS • When a capacitor is charged by a battery in series with a resistor, the current and capacitor charge are not constant. • The charge approaches its final value asymptotically and the current approaches zero asymptotically. R-C CIRCUITS • After a time 𝜏 = 𝑅𝐶, the charge has approached within 1/𝑒 of its final value. • This time is called the time constant or relaxation time of the circuit. R-C CIRCUITS • When the capacitor discharges, the charge and current are given as functions of time. • The time constant is the same for charging and discharging. R-C CIRCUITS • Capacitor charging: 𝑞 = 𝐶𝜀 1 − 𝑒 −𝑡/𝑅𝐶 𝑡 − 𝑒 𝑅𝐶 ) = 𝑄𝑓 (1 − 𝑑𝑞 𝜀 −𝑡 𝑖= = 𝑒 𝑑𝑡 𝑅 −𝑡 𝑅𝐶 = 𝐼0 𝑒 𝑅𝐶 R-C CIRCUITS • Capacitors discharging: −𝑡 𝑅𝐶 𝑞 = 𝑄0 𝑒 𝑑𝑞 𝑄0 −𝑡 𝑖= =− 𝑒 𝑑𝑡 𝑅𝐶 −𝑡 𝑅𝐶 = 𝐼0 𝑒 𝑅𝐶 HOUSEHOLD WIRING • In household wiring systems, the various electrical devices are connected in parallel across the power line, which consists of a pair of conductors, one “hot” and the other “neutral”. • An additional “ground” wire is included for safety. HOUSEHOLD WIRING • The maximum permissible current in a circuit is determined by the size of the wires and the maximum temperature they can tolerate. • Protection against excessive current and the resulting fire hazard is provided by fuses or circuit breakers.