* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download UoB-TS-Structure1
Colloidal crystal wikipedia , lookup
Viscoplasticity wikipedia , lookup
Euler–Bernoulli beam theory wikipedia , lookup
Strengthening mechanisms of materials wikipedia , lookup
Fatigue (material) wikipedia , lookup
Paleostress inversion wikipedia , lookup
Deformation (mechanics) wikipedia , lookup
Hooke's law wikipedia , lookup
Viscoelasticity wikipedia , lookup
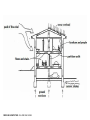
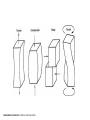
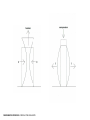
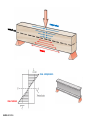
Pantheon, Rome (126CE) UNIVERSITY OF BEDFORDSHIRE: EAST LONDON: ARCHITECTURE TECHNICAL STUDIES YEAR 1TECHNICAL 1 TECHNICALSTUDIES STUDIES 1. Structure & Form ‘The Architect/Designer and the Structural Engineer’ January-February 2. Climate & Shelter ‘The Architect/Designer and the Environment & Services Engineer’ February-March 3. Construction ‘The Architect/Designer and the Builder’ March-April 4. Case Studies In practice May TECHNICAL STUDIES: LECTURE SERIES Pete Silver and Will McLean, Introduction to Architectural Technology (London: Laurence King, 2008) Francis D.K.Ching , A Visual Dictionary of Architecture (New York: Van Nostrand Reinhold, 1997) Derek Osbourn , rev. Roger Greeno, Mitchell’s: Introduction to Building, 2nd ed. (Harlow: Longman, 1997) Jack Stroud Foster and Roger Greeno, Mitchell’s: Structure & Fabric, Part 1, 7th ed. (Harlow: Prentice Hall, 2007) Jack Stroud Foster, Raymond Harington and Roger Greeno , Mitchell’s: Structure & Fabric, Part 2, 7th ed. (Harlow: Pearson Prentice Hall, 2007) Alan Everett, rev. C.M.H. Barritt, Mitchell’s: Materials, 5th ed. (Abingdon: Routledge, 2013) Peter Burberry, Mitchells: Environment and Services, 8th ed. (Harlow: Longman, 1997) Alan Blanc, Mitchell’s: Internal Components (Harlow: Longman, 1994) Michael McEvoy, Mitchell’s Building Series: External Components (Abingdon: Routledge, 2014) Yvonne Dean, Mitchell’s Building Series: Finishes, 4th ed. (Abingdon: Routledge, 2014) Yvonne Dean, Mitchell’s: Materials Technology (Harlow: Longman, 1996) J. B. McKay, McKay’s Building Construction (Shaftesbury: Donhead, 2005); also available as separate volumes Sophie Pelsmakers, The Environment Design Pocketbook (London: RIBA, 2012) Charlotte Baden-Powell, Jonathan Hetreed and Ann Ross, Architect’s Pocket Book, 4th ed. (Oxford: Architectural Press, 2011) Matthys Levy and Mario Salvadori, Why Buildings Stand Up: The Strength of Architecture(London: W.W. Norton, 1990) Matthys Levy and Mario Salvadori, Why Buildings Fall Down: How Structures Fail (London: W.W. Norton, 1992) Austin Williams, Shortcuts: Book 1: Structure and Fabric (London: RIBA, 2008) Austin Williams, Shortcuts: Book 2: Sustainability and Practice(London: RIBA, 2008) RECOMMENDED READING: BOOKS Architects’ Journal RECOMMENDED READING: MAGAZINES / SERIES Architects’ Working Details (Architect’s Journal/EMAP) Detail magazine RECOMMENDED READING: MAGAZINES / SERIES LECTURE 1: INTRODUCTION TO STRUCTURAL PRINCIPLES, BEAMS AND COLUMNS LECTURE 2: BEARING WALLS, FOUNDATIONS AND STRUCTURAL OPENINGS LECTURE 3: TRUSSES, FRAME STRUCTURES AND SLABS LECTURE 4: COMPLEX STRUCTURAL SYSTEMS LECTURE SERIES 1: STRUCTURE AND FORM STRUCTURAL SYSTEMS IN NATURE STRUCTURAL SYSTEMS IN NATURE STRUCTURAL SYSTEMS IN NATURE STRUCTURAL SYSTEMS IN NATURE King’s Cross Station, London by John McAslan & Partners, 2012 STRUCTURAL SYSTEMS IN ARCHITECTURE St Chapelle, Paris, 13th century FORCES IN ARCHITECTURE: LIVE AND DEAD LOADS FORCES IN ARCHITECTURE: EQUILIBRIUM Sir Isaac Newton (1643-1727) 1. A body remains at rest or in motion with a constant velocity in a straight line unless an external force acts on it (Law of Inertia) 2. Force (Newton) = Mass (kg) x Acceleration (m/s2) (Gravity on earth = approx. 9.8m/s2) 3. For every force acting on a body, the body exerts a force having equal magnitude in the opposite direction (Law of Action and Reaction) FUNDAMENTAL PRINCIPLES: NEWTON’S LAWS OF MOTION FUNDAMENTAL PRINCIPLES: FORCES ACTING ON A BODY FUNDAMENTAL PRINCIPLES: FORCES ACTING ON A BODY f (stress) = P (force) / A (area) UNITS: N/mm2 (1 Pascal (Pa) = 1 N/m2) FUNDAMENTAL PRINCIPLES: STRESS Materials react to stress by distributing it in such a way that there is an equal balance of internal forces. The result is a change in the form of the structure, equal to: Change in size (∆L) Strain = Original size (L) UNITS: % or decimal FUNDAMENTAL PRINCIPLES: STRAIN (yield point) Elastic deformation – internal structures remain the same, but are stretched when a stress is applied, returning to their original shape when the stress is removed. Plastic deformation – internal structures deform to a new shape when stress is applied (e.g. lead) – a material that experiences little plastic deformation is brittle The ability of a material to resist elastic deformation (prior to failure) determines its strength. FUNDAMENTAL PRINCIPLES: ELASTIC AND PLASTIC DEFORMATION strong material (yield point) weak material Young’s Modulus, or ‘Modulus of Elasticity’, defines the stiffness/flexibility of a material Young’s Modulus = Stress Strain FUNDAMENTAL PRINCIPLES: STIFFNESS / FLEXIBILITY [UNITS: N/m2 (Pa)] A stiff material has a high Young’s Modulus; a flexible material has a low Young’s Modulus (stiffness) Stiffness tends to increase with material density (with some exceptions) FUNDAMENTAL PRINCIPLES: STIFFNESS AND DENSITY Pathenon, Athens, 5th century BC Abbé Marc-Antoine Laugier: Essai sur l'Architecture [Essay on Architecture], 1755 frontispiece COLUMN AND BEAM: ORGINS AND ARCHITECTURE BEAMS Transfer of Loads Turning Moments Bending Deflection (Shear) Active force/load Transfer of load to supports Reaction BEAMS: TRANSFER OF LOADS Reaction Turning moment = w (force) x L (lever arm) UNITS: Nm (Newton metres) BEAMS: TURNING MOMENTS max. compression max. tension BEAMS: BENDING resisting moment in wall bending moment created by load 1. CANTILEVER BEAM deflection 2. SINGLE SPAN BEAM bending moments equal and opposite create equilibrium The depth of the beam is critical to minimise stresses and to maximise the beam’s efficiency. BEAMS: BENDING AND DEFLECTION T C C T BEAMS: SHEAR COLUMNS Buckling Effective Height Eccentric Loading • The more slender a column, the greater its tendency to buckle. • Buckling can occur in any direction, so column sections are ideally round or square hollow sections with material concentrated on the outside edges (as with the flanges of a steel beam) COLUMNS: BUCKLING COLUMNS: EFFECTIVE HEIGHT • Loads should usually be concentrated in the middle third of the horizontal section of the column to prevent tensile stresses developing COLUMNS: ECCENTRIC LOADING Material Max. tensile stress (N/mm2) Max. compressive stress (N/mm2) Young’s Modulus (kN/mm2) Steel 300 300 200 Timber 60 30 10 Stone 1 100 50 Concrete 5 50 30 Brickwork 1 20 20 Aluminium 300 300 70 Glass 5 175 70 INTRODUCTION TO STRUCTURAL PRINCIPLES, BEAMS AND COLUMNS : MATERIAL CHARACTERISTICS COMPOSITE BEAMS: CONCRETE BEAMS WITH STEEL REINFORCEMENT COMPOSITE BEAMS: POST-TENSIONG CONCRETE BEAMS CONCRETE BEAMS: BEAM AND BLOCK FLOOR STRUCTURE TIMBER BEAMS: TRADITIONAL AND MODERN TIMBER BEAMS: CONCRETE AND STONE LINTELS TIMBER BEAMS: STEEL LINTEL AND TIMBER FLOOR JOISTS TYPICAL BEAM SPANS Rolled steel sections Span : Depth Ratio 20:1 Timber floor joists (50mm wide, 450mm centres) Depth = (Span+25mm)/25 Glulam beams Span: Depth ratio 18:1 Reinforced concrete floor beams Span : Depth ratio 23:1 BEAMS: TYPICAL SPANS Nordic Pavilion, Venice Biennale Sverre Fehn, 1957 Nordic Pavilion, Venice Biennale Sverre Fehn, 1957 Nordic Pavilion, Venice Biennale Sverre Fehn, 1957 S.R. Crown Hall, Illinois Institute of Technology, Chicago Ludwig Mies van der Rohe, 1956 John Hope Gateway Centre at Royal Botanic Gardens, Edinburgh Edward Cullinan Architects, 2010 John Hope Gateway Centre at Royal Botanic Gardens, Edinburgh Edward Cullinan Architects, 2010 John Hope Gateway Centre at Royal Botanic Gardens, Edinburgh Edward Cullinan Architects, 2010 f (STRESS) = P (force) / A (area) SUMMARY • Structural Systems in Nature • Structural Systems in Architecture • Forces in Architecture: • Fundamental Principles: Live and Dead Loads Equilibrium Newton’s Laws of Motion Forces Acting on a Body Stress Strain Elastic and Plastic Deformation Stiffness and Flexibility • Column and Beam: Origins and Architecture • Beams: • Columns: Transfer of Loads Turning Moments Bending Deflection Shear Buckling Effective Height Eccentric Loading UNITS: N/mm2 (1 Pascal (Pa) = 1 N/m2) STRAIN = Change in size (∆L) Original size (L) UNITS: % or decimal YOUNG’S = Stress Strain MODULUS UNITS: N/mm2 (Pa) A stiff material has a high Young’s Modulus; a flexible material has a low Young’s Modulus Turning moment = w (force) x UNITS: Nm L (lever arm) NEWTON’S LAWS OF MOTION 1. A body remains at rest or in motion with a constant velocity in a straight line unless an external force acts on it 2. Force (Newton) = Mass (kg) x Acceleration (m/s2) (Gravity on earth = approx. 9.8m/s2) 3. For every force acting on a body, the body exerts a force having equal magnitude in the opposite direction UNIVERSITY OF EAST INTRODUCTION TO STRUCTURAL LONDON: ARCHITECTURE PRINCIPLES, BEAMS AND COLUMNS : SUMMARY YEAR 1 TECHNICAL STUDIES