* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download KEY - Rose
Survey
Document related concepts
Transcript
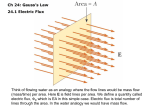
Physics II Homework VIII CJ Chapter 27; 2, 9, 12, 22, 29, 39, 51 27.2. Visualize: 27.9. Model: The electric field is uniform over the entire surface. Visualize: Please refer to Figure Ex27.9. The electric field vectors make an angle of 30 below the surface. Because the normal n̂ to the planar surface is at an angle of 90 relative to the surface, the angle between n̂ and E is 120. Solve: The electric flux is e E A EA cos 200 N/C 1.0 10 2 m2 cos120 1.0 N m 2 /C 27.12. Model: The electric field over the rectangle in the xz plane is uniform. Solve: (a) The area vector is perpendicular to the xz plane. Thus A 2.0 cm 3.0 cm ˆj 6.0 10 4 m2 ˆj The electric flux through the rectangle is N m /C iˆ ˆj 600 10 N m /C kˆ ˆj 0 N m /C e E A 50iˆ 100kˆ N/C 6.0 10 4 m 2 ˆj 300 10 4 4 2 (b) The flux is 2 2 e E A 50iˆ 100ˆj N/C 6.0 10 4 m 2 ˆj 0 N m /C 0.06 N m /C 0.06 N m /C 300 10 4 N m 2 /C iˆ ˆj 600 10 4 N m 2 /C ˆj ˆj 2 2 2 27.22. Visualize: Please refer to Figure Ex27.22. For any closed surface that encloses a total charge Qin, the net electric flux through the closed surface is e Qin 0 . For the closed surface of the torus, Qin includes only the 1 nC charge. So, the net flux through the torus is due to this charge: e This is inward flux. 1 109 C 113 N m2 /C 8.85 10 12 C2 /Nm2 27.29. Model: Because the tetrahedron contains no charge, the net flux through the tetrahedron is zero. Visualize: Solve: (a) The area of the base of the tetrahedron is 3 4 a2 , where a 20 cm is the length of one of the sides. Because the base of the tetrahedron is parallel to the ground and the vertical uniform electric field passes upward through the base, the angle between E and A is 180. Thus, base E Abase EAbase cos180 E 2 3 2 3 a 200 N/C 0.20 m 3.46 N m2 /C 4 4 (b) Since E is perpendicular to the base, the other three sides of the tetrahedron share the flux equally. Because the tetrahedron contains no charge, net base 3 side 0 N m2 / C 3.46 N m2 /C 3 side 0 N m 2 / C side 1.15 N m 2 /C 27.39. Model: The excess charge on a conductor resides on the outer surface. The charge distribution on the two spheres is assumed to have spherical symmetry. Visualize: Please refer to Figure P27.39. The Gaussian surfaces with radii r 8 cm, 10 cm, and 17 cm match the symmetry of the charge distribution. So, E is perpendicular to these Gaussian surfaces and the field strength has the same value at all points on the Gaussian surface. Solve: (a) Gauss’s law is e E dA Qin 0 . Applying it to a Gaussian surface of radius 8 cm, 2 Qin 0 EAsphere 8.85 1012 C2/N m2 15,000 N/C 4 0.08 m 1.068 108 C Because the excess charge on a conductor resides on its outer surface and because we have a solid metal sphere inside our Gaussian surface, Qin is the charge that is located on the exterior surface of the inner sphere. (b) In electrostatics, the electric field within a conductor is zero. Applying Gauss’s law to a Gaussian surface just inside the inside-surface of the hollow sphere at r 10 cm, Q e E dA in Qin 0 C 0 That is, there is no net charge. Because the inner sphere has a charge of 1.068 108 C, the inside surface of the hollow sphere must have a charge of 1.068 108 C. (c) Applying Gauss’s law to a Gaussian surface at r 17 cm, Qin 0 E dA 0 EAsphere 8.85 1012 C2 /Nm2 15,000 N/C 4 0.17 m 4.82 108 C 2 This value includes the charge on the inner sphere, the charge on the inside surface of the hollow sphere, and the charge on the exterior surface of the hollow sphere due to polarization. Thus, Qexterior hollow 1.068 108 C 1.068 10 8 C 4.82 10 8 C 8 Qexterior hollow 4.82 10 C 27.51. Model: A long, charged cylinder is assumed to be infinite and to have linear symmetry. Visualize: The cylindrical symmetry of the situation indicates that the only possible shape of the electric field is to point straight in or out from the cylinder. The shape of the field suggests that we choose our Gaussian surface to be a cylinder of radius r and length L, which is concentric with the charged cylinder. Solve: (a) For r R, Gauss’s law is E dA left E dA right 0 N m2 / C 0 N m2 / C EA Qin 0 E dA wall E E dA Qin 0 L E 2 rL 0 2 0r 2 0 1 rˆ r (b) For r R, Gauss’s law is EA Qin 0 E r 2L Qin A 0 2 rL 0 An expression for the volume charge density in terms of the linear charge density can be calculated by considering the charge on a cylinder of length d and radius R: d R2d R2 1 r 1 r r 2L E E rˆ 2 2 2 0 R2 R 2 rL 0 2 0 R (c) At r R, Er R 1 R 1 rˆ rˆ 2 2 0 R 2 0 R