Download Lecture 25 - UConn Physics

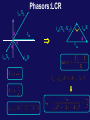
Physics 1502: Lecture 25
Today’s Agenda
• Announcements:
• Midterm 2: NOT Nov. 6
– Following week …
• Homework 07: due Friday next week
• AC current
– Resonances
• Electromagnetic Waves
– Maxwell’s Equations - Revised
– Energy and Momentum in Waves
R
C
e
~
L
w
i m wL

im
wC

em

im R
Phasors:LCR
i m XL
em


i m XC


im R
i m (XL-X C)
em
im R


Phasors:Tips
y
• This phasor diagram was drawn as a
snapshot of time t=0 with the voltages
being given as the projections along the
y-axis.
• Sometimes, in working problems, it is
easier to draw the diagram at a time when
the current is along the x-axis (when i=0).
em

i mR
imXC
em


i m XC
i mX L
i m XL

x
im R
From this diagram, we can also create a
triangle which allows us to calculate the
impedance Z:
Z
| XL-XC |
| 
R
“Full Phasor Diagram”
“ Impedance Triangle”
Resonance
The current in an LCR circuit depends on the values
of the elements and on the driving frequency through
the relation
Z
| XL-XC |
| 
R
“ Impedance Triangle”
Suppose you plot the current
versus w, the source voltage
frequency, you would get:
em / R 0
R=Ro
im
R=2Ro
0
0
1
wx
2w2o
Power and Resonance in RLC
• Power, as well as current, peaks at w= w 0. The sharpness
of the resonance depends on the values of the
components.
• Recall:
Z
| 
• Therefore,
| XL-XC |
R
We can write this in the following manner (which we won’t try to
prove):
…introducing the curious factors Q and x
The Q factor
Q also determines the sharpness of the resonance peaks in
a graph of Power delivered by the source versus frequency.
Pav
High Q
Dw
wo
Low Q
w
Lecture 25, ACT 1
• Consider the two circuits shown
where CII = 2 CI.
– What is the relation between the
quality factors, QI and QII , of the
two circuits?
(a) QII < QI
(b) QII = QI
R
R
CI
e
~
L
CII
e
~
(c) QII > QI
L
Lecture 25, ACT 2
• Consider the two circuits shown where
CII = 2 CI and LII = ½ LI.
– Which circuit has the narrowest width
of the resonance peak?
(a) I
(b) II
R
R
CI
e
~
L
CII
e
~
L
(c) Both the same
Power Transmission
• How do we transport power from power stations to homes?
– At home, the AC voltage obtained from outlets in this country is
120V at 60Hz.
– Transmission of power is typically at very high voltages
( eg
~500 kV) (a “high tension” line)
– Transformers are used to raise the voltage for transmission and
lower the voltage for use. We’ll describe these next.
• But why?
– Calculate ohmic losses in the transmission lines:
– Define efficiency of transmission:
Keep R
small
– Note for fixed input power and line resistance, the
inefficiency  1/V2
Make
Vin big
Transformers
• AC voltages can be stepped up
or stepped down by the use of
transformers.
• The AC current in the primary
circuit creates a time-varying e
magnetic field in the iron
• This induces an emf on the
secondary windings due to the
mutual inductance of the two sets
of coils.
iron
~
V1
V2
N1
(primary)
N2
(secondary)
• The iron is used to maximize the mutual inductance. We
assume that the entire flux produced by each turn of the
primary is trapped in the iron.
Ideal
No resistance losses
Transformers (no load)
All flux contained in iron
Nothing connected on secondary
• The primary circuit is just an AC voltage
source in series with an inductor. The change
in flux produced in each turn is given by:
iron
e
~
• The change in flux per turn in the secondary coil is the
same as the change in flux per turn in the primary coil
(ideal case). The induced voltage appearing across the
secondary coil is given by:
V1
V2
N1
(primary)
N2
(secondary)
• Therefore,
• N2 > N1  secondary V2 is larger than primary V1 (step-up)
• N1 > N2  secondary V2 is smaller than primary V1 (step-down)
• Note: “no load” means no current in secondary. The primary current,
termed “the magnetizing current” is small!
Ideal
Transformers with a Load
• What happens when we connect a
resistive load to the secondary coil?
– Flux produced by primary coil induces e
an emf in secondary
– emf in secondary produces current i2
iron
~
V1
V2
N1
(primary)
– This current produces a flux in the
secondary coil N2i2,which opposes
the original flux -- Lenz’s law
– This changing flux appears in the
primary circuit as well; the sense of it
is to reduce the emf in the primary...
– However, V1 is a voltage source.
– Therefore, there must be an increased
current i1 (supplied by the voltage
source) in the primary which produces
a flux  N1i1 which exactly cancels the
flux produced by i2.
N2
(secondary)
R
Transformers with a Load
iron
• With a resistive load in the secondary,
the primary current is given by:
e
~
V1
V2
N1
(primary)
It’s time..
3
N2
(secondary)
R
iron
Lecture 25, ACT 3
• The primary coil of an ideal transformer is
connected to a battery (V1 = 12V) as shown.
The secondary winding has a load of 2 W.
There are 50 turns in the primary and 200
turns in the secondary.
e
– What is the current in the secondcary ?
(a) 24 A
(b) 1.5 A
(c) 6 A
V1
V2
N1
(primary)
N2
(secondary)
(d) 0 A
R
iron
Lecture 25, ACT 4
• The primary coil of an ideal transformer is
e
connected to the wall (V1 = 120V) as shown.
There are 50 turns in the primary and 200
turns in the secondary.
~
V1
V2
N1
– If 960 W are dissipated in the resistor
R, what is the current in the primary ?
(a) 8 A
(b) 16 A
(primary)
(c) 32 A
N2
(secondary)
R
Fields from Circuits?
• We have been focusing on what happens within the circuits we have
been studying (eg currents, voltages, etc.)
• What’s happening outside the circuits??
– We know that:
» charges create electric fields and
» moving charges (currents) create magnetic fields.
– Can we detect these fields?
– Demos:
» We saw a bulb connected to a loop glow when the loop came
near a solenoidal magnet.
» Light spreads out and makes interference patterns.
Do we understand this?
f( x
f( x )
x
x
z
y
Maxwell’s Equations
• These equations describe all of Electricity and
Magnetism.
• They are consistent with modern ideas such as
relativity.
• They describe light !
Maxwell’s Equations - Revised
• In free space, outside the wires of a circuit, Maxwell’s equations
reduce to the following.
• These can be solved (see notes) to give the following
differential equations for E and B.
• These are wave equations. Just like for waves on a
string. But here the field is changing instead of the
displacement of the string.
Plane Wave Derivation
Step 1
Assume we have a plane wave propagating in z (ie E, B
not functions of x or y)
Example:
Step 2
does this
Apply Faraday’s Law to infinitesimal loop in x-z plane
x
Ex
Ex
z1
By
y
DZ
z2
Dx
z
Plane Wave Derivation
Step 3
Apply Ampere’s Law to an infinitesimal loop in the y-z
plane:
x
Ex
DZ
z1 z2
z
y
Step 4
By
By
Dy
Combine results from steps 2 and 3 to eliminate By
!!
Plane Wave Derivation
• We derived the wave eqn for Ex:
• We could have also derived for By:
• How are Ex and By related in phase and magnitude?
– Consider the harmonic solution:
where
(Result from step 2)
• By is in phase with Ex
• B0 = E0 / c
Review of Waves from last semester
• The one-dimensional wave equation:
has a general solution of the form:
where h1 represents a wave traveling in the +x direction and h2
represents a wave traveling in the -x direction.
• A specific solution for harmonic waves traveling in the +x
direction is:
h l
A
x
A = amplitude
l = wavelength
f = frequency
v = speed
k = wave number
E & B in Electromagnetic Wave
• Plane Harmonic Wave:
where:
y
x
2
z
Note: the direction of propagation
where
is given by the cross product
are the unit vectors in the (E,B) directions.
Nothing special about (Ey,Bz); eg could have (Ey,-Bx)
Note cyclical relation:
Lecture 25, ACT 5
• Suppose the electric field in an e-m wave is given by:
5A
– In what direction is this wave traveling ?
(a) + z direction
(c) +y direction
(b) -z direction
(d) -y direction
Lecture 25, ACT 5
• Suppose the electric field in an e-m wave is given
by:
5B
• Which of the following expressions describes
the magnetic field associated with this wave?
(a) Bx = -(Eo/c)cos(kz + wt)
(b) Bx = +(Eo/c)cos(kz - wt)
(c) Bx = +(Eo/c)sin(kz - wt)
Velocity of Electromagnetic Waves
• The wave equation for Ex:
(derived from Maxwell’s Eqn)
• Therefore, we now know the velocity of
electromagnetic waves in free space:
• Putting in the measured values for m0 & e0, we get:
• This value is identical to the measured speed of light!
– We identify light as an electromagnetic wave.
The EM Spectrum
• These EM waves can take on any wavelength from
angstroms to miles (and beyond).
• We give these waves different names depending on the
wavelength.
10-14
10-10
10-6
10-2 1 102
Wavelength [m]
106
1010
Energy in EM Waves / review
• Electromagnetic waves contain energy which is stored in E
and B fields:
=
• Therefore, the total energy density in an e-m wave = u, where
• The Intensity of a wave is defined as the average power
transmitted per unit area = average energy density times wave
velocity: