* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Lecture 25 - UConn Physics
Lorentz force wikipedia , lookup
Friction-plate electromagnetic couplings wikipedia , lookup
Scanning SQUID microscope wikipedia , lookup
Three-phase electric power wikipedia , lookup
Maxwell's equations wikipedia , lookup
Wireless power transfer wikipedia , lookup
Electromagnetism wikipedia , lookup
Power engineering wikipedia , lookup
Magnetic core wikipedia , lookup
Mains electricity wikipedia , lookup
High voltage wikipedia , lookup
Faraday paradox wikipedia , lookup
Opto-isolator wikipedia , lookup
Induction heater wikipedia , lookup
Electromagnetic radiation wikipedia , lookup
Electromotive force wikipedia , lookup
History of electric power transmission wikipedia , lookup
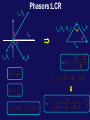
Physics 1502: Lecture 25 Today’s Agenda • Announcements: • Midterm 2: NOT Nov. 6 – Following week … • Homework 07: due Friday next week • AC current – Resonances • Electromagnetic Waves – Maxwell’s Equations - Revised – Energy and Momentum in Waves R C e ~ L w i m wL im wC em im R Phasors:LCR i m XL em i m XC im R i m (XL-X C) em im R Phasors:Tips y • This phasor diagram was drawn as a snapshot of time t=0 with the voltages being given as the projections along the y-axis. • Sometimes, in working problems, it is easier to draw the diagram at a time when the current is along the x-axis (when i=0). em i mR imXC em i m XC i mX L i m XL x im R From this diagram, we can also create a triangle which allows us to calculate the impedance Z: Z | XL-XC | | R “Full Phasor Diagram” “ Impedance Triangle” Resonance The current in an LCR circuit depends on the values of the elements and on the driving frequency through the relation Z | XL-XC | | R “ Impedance Triangle” Suppose you plot the current versus w, the source voltage frequency, you would get: em / R 0 R=Ro im R=2Ro 0 0 1 wx 2w2o Power and Resonance in RLC • Power, as well as current, peaks at w= w 0. The sharpness of the resonance depends on the values of the components. • Recall: Z | • Therefore, | XL-XC | R We can write this in the following manner (which we won’t try to prove): …introducing the curious factors Q and x The Q factor Q also determines the sharpness of the resonance peaks in a graph of Power delivered by the source versus frequency. Pav High Q Dw wo Low Q w Lecture 25, ACT 1 • Consider the two circuits shown where CII = 2 CI. – What is the relation between the quality factors, QI and QII , of the two circuits? (a) QII < QI (b) QII = QI R R CI e ~ L CII e ~ (c) QII > QI L Lecture 25, ACT 2 • Consider the two circuits shown where CII = 2 CI and LII = ½ LI. – Which circuit has the narrowest width of the resonance peak? (a) I (b) II R R CI e ~ L CII e ~ L (c) Both the same Power Transmission • How do we transport power from power stations to homes? – At home, the AC voltage obtained from outlets in this country is 120V at 60Hz. – Transmission of power is typically at very high voltages ( eg ~500 kV) (a “high tension” line) – Transformers are used to raise the voltage for transmission and lower the voltage for use. We’ll describe these next. • But why? – Calculate ohmic losses in the transmission lines: – Define efficiency of transmission: Keep R small – Note for fixed input power and line resistance, the inefficiency 1/V2 Make Vin big Transformers • AC voltages can be stepped up or stepped down by the use of transformers. • The AC current in the primary circuit creates a time-varying e magnetic field in the iron • This induces an emf on the secondary windings due to the mutual inductance of the two sets of coils. iron ~ V1 V2 N1 (primary) N2 (secondary) • The iron is used to maximize the mutual inductance. We assume that the entire flux produced by each turn of the primary is trapped in the iron. Ideal No resistance losses Transformers (no load) All flux contained in iron Nothing connected on secondary • The primary circuit is just an AC voltage source in series with an inductor. The change in flux produced in each turn is given by: iron e ~ • The change in flux per turn in the secondary coil is the same as the change in flux per turn in the primary coil (ideal case). The induced voltage appearing across the secondary coil is given by: V1 V2 N1 (primary) N2 (secondary) • Therefore, • N2 > N1 secondary V2 is larger than primary V1 (step-up) • N1 > N2 secondary V2 is smaller than primary V1 (step-down) • Note: “no load” means no current in secondary. The primary current, termed “the magnetizing current” is small! Ideal Transformers with a Load • What happens when we connect a resistive load to the secondary coil? – Flux produced by primary coil induces e an emf in secondary – emf in secondary produces current i2 iron ~ V1 V2 N1 (primary) – This current produces a flux in the secondary coil N2i2,which opposes the original flux -- Lenz’s law – This changing flux appears in the primary circuit as well; the sense of it is to reduce the emf in the primary... – However, V1 is a voltage source. – Therefore, there must be an increased current i1 (supplied by the voltage source) in the primary which produces a flux N1i1 which exactly cancels the flux produced by i2. N2 (secondary) R Transformers with a Load iron • With a resistive load in the secondary, the primary current is given by: e ~ V1 V2 N1 (primary) It’s time.. 3 N2 (secondary) R iron Lecture 25, ACT 3 • The primary coil of an ideal transformer is connected to a battery (V1 = 12V) as shown. The secondary winding has a load of 2 W. There are 50 turns in the primary and 200 turns in the secondary. e – What is the current in the secondcary ? (a) 24 A (b) 1.5 A (c) 6 A V1 V2 N1 (primary) N2 (secondary) (d) 0 A R iron Lecture 25, ACT 4 • The primary coil of an ideal transformer is e connected to the wall (V1 = 120V) as shown. There are 50 turns in the primary and 200 turns in the secondary. ~ V1 V2 N1 – If 960 W are dissipated in the resistor R, what is the current in the primary ? (a) 8 A (b) 16 A (primary) (c) 32 A N2 (secondary) R Fields from Circuits? • We have been focusing on what happens within the circuits we have been studying (eg currents, voltages, etc.) • What’s happening outside the circuits?? – We know that: » charges create electric fields and » moving charges (currents) create magnetic fields. – Can we detect these fields? – Demos: » We saw a bulb connected to a loop glow when the loop came near a solenoidal magnet. » Light spreads out and makes interference patterns. Do we understand this? f( x f( x ) x x z y Maxwell’s Equations • These equations describe all of Electricity and Magnetism. • They are consistent with modern ideas such as relativity. • They describe light ! Maxwell’s Equations - Revised • In free space, outside the wires of a circuit, Maxwell’s equations reduce to the following. • These can be solved (see notes) to give the following differential equations for E and B. • These are wave equations. Just like for waves on a string. But here the field is changing instead of the displacement of the string. Plane Wave Derivation Step 1 Assume we have a plane wave propagating in z (ie E, B not functions of x or y) Example: Step 2 does this Apply Faraday’s Law to infinitesimal loop in x-z plane x Ex Ex z1 By y DZ z2 Dx z Plane Wave Derivation Step 3 Apply Ampere’s Law to an infinitesimal loop in the y-z plane: x Ex DZ z1 z2 z y Step 4 By By Dy Combine results from steps 2 and 3 to eliminate By !! Plane Wave Derivation • We derived the wave eqn for Ex: • We could have also derived for By: • How are Ex and By related in phase and magnitude? – Consider the harmonic solution: where (Result from step 2) • By is in phase with Ex • B0 = E0 / c Review of Waves from last semester • The one-dimensional wave equation: has a general solution of the form: where h1 represents a wave traveling in the +x direction and h2 represents a wave traveling in the -x direction. • A specific solution for harmonic waves traveling in the +x direction is: h l A x A = amplitude l = wavelength f = frequency v = speed k = wave number E & B in Electromagnetic Wave • Plane Harmonic Wave: where: y x 2 z Note: the direction of propagation where is given by the cross product are the unit vectors in the (E,B) directions. Nothing special about (Ey,Bz); eg could have (Ey,-Bx) Note cyclical relation: Lecture 25, ACT 5 • Suppose the electric field in an e-m wave is given by: 5A – In what direction is this wave traveling ? (a) + z direction (c) +y direction (b) -z direction (d) -y direction Lecture 25, ACT 5 • Suppose the electric field in an e-m wave is given by: 5B • Which of the following expressions describes the magnetic field associated with this wave? (a) Bx = -(Eo/c)cos(kz + wt) (b) Bx = +(Eo/c)cos(kz - wt) (c) Bx = +(Eo/c)sin(kz - wt) Velocity of Electromagnetic Waves • The wave equation for Ex: (derived from Maxwell’s Eqn) • Therefore, we now know the velocity of electromagnetic waves in free space: • Putting in the measured values for m0 & e0, we get: • This value is identical to the measured speed of light! – We identify light as an electromagnetic wave. The EM Spectrum • These EM waves can take on any wavelength from angstroms to miles (and beyond). • We give these waves different names depending on the wavelength. 10-14 10-10 10-6 10-2 1 102 Wavelength [m] 106 1010 Energy in EM Waves / review • Electromagnetic waves contain energy which is stored in E and B fields: = • Therefore, the total energy density in an e-m wave = u, where • The Intensity of a wave is defined as the average power transmitted per unit area = average energy density times wave velocity: