Download The magnetic forces on the two sides parallel to the x axis balance

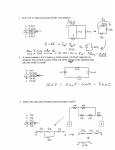
Physics 2 (9 CFU)
Name
Surname
Exercise n.1
A.A. 2011-2012
n. matricola
3.9.2012
A small sphere having mass 1g and charge Q, is hanging from a wire that forms and angle θ=15° with a vertical
plate of indefinite extension bearing a surface charge density σ=10 -8C/m2. Find the charge Q.
The sphere is in equilibrium under the action of the weight force and the electrostatic force:
𝜎𝑄
2𝜀0 𝑚𝑔
Therefore:
2𝜀0 𝑚𝑔
𝑄=
≅ 1.7 × 10−5 𝐶
𝜎
𝑡𝑔(𝜃) =
Exercise n. 2
Find an expression for the electrical resistance of a thin conducting sheet, consisting of a
material of resistivity ρ, having a trapezoidal shape (see figure) with height H, thickness t,
minor basis B2 and larger basis B1. Show that if B1-B2<<B2 this expression is the same as
for a rectangular sheet having the same height H and basis (
𝐵2+𝐵1
2
).
To calculate the overall resistance we must ideally divide the sheet in a large number of rectangular resistors
having height dy and width L(y), with
𝐵2 − 𝐵1
𝐿(𝑦) =
𝑦 + 𝐵1
𝐻
For the whole trapezoidal sheet the overall resistance is:
𝜌 𝐻 𝑑𝑦
𝜌 𝐻
𝑑𝑦
𝜌
𝐻
𝐵2
𝑅= ∫
= ∫
=
𝑙𝑛 ( )
𝐵2
−
𝐵1
𝑡 0 𝐿(𝑦) 𝑡 0
𝐵1
𝑦 + 𝐵1 𝑡 𝐵2 − 𝐵1
𝐻
t is the sheet thickness.
𝐵2
𝐵1
𝐵1−𝐵2
𝐵2−𝐵1
If 𝐵1 − 𝐵2 ≪ 𝐵2 then 𝑙𝑛 ( ) = 𝑙𝑛 ( −
)≅
Therefore: 𝑅 =
𝜚 𝐻
𝐵1
𝐵1
𝐵1
𝐵1
𝑡 𝐵1
That is, exactly the same resistance as for a rectangular sheet having the same height H and basis (
𝐵2+𝐵1
2
)
Exercise n. 3
A conducting square loop (side length d=10 cm) lies in the xy vertical plane, as shown in
the figure. The loop has a linear mass density of 1 g cm-1. The weight force acts on the loop
along the x direction. A magnetic field B is applied along the z direction. The magnetic
⃗ = 𝐾𝑥𝑘̂ , K=0.1 T/cm and 𝑘̂ is the unit vector of the
field varies according the expression: 𝐵
z axis. Calculate the current i that must flow along the loop to balance the weight force.
The magnetic forces on the two sides parallel to the x axis balance out. The force on the side lying on the y
axis is zero because the magnetic field is zero. The only unbalanced force acts upward on the side parallel to
the y axis at a distance d, where the magnetic field is 1 T.
The equilibrium conditions are:
𝒚𝒊𝒆𝒍𝒅𝒔
𝒊𝒍𝑩 = 𝟒𝝆𝒍𝒈 →
𝒊=
𝟒𝝆𝒈
𝑩
≅𝟒𝑨
Exercise n. 4
An electron having a kinetic energy of 10 keV moves along the x axis
in a region a) of zero potential energy. At a certain point the electron
hits an energy barrier of 6 keV. Calculate the wavelength associated to
the electron in the region b).
In the region a the wavelength is related to the kinetic energy by:
ℎ2
𝐾𝑎 =
2𝑚𝜆2𝑎
In the region b we have:
ℎ2
𝐾𝑏 = 𝐾𝑎 − 𝑈 =
2𝑚𝜆2𝑏
Therefore
ℎ
𝜆𝑏 =
≅ 0.16 Å
√2𝑚(𝐾𝑎 − 𝑈)