Download Electromagnetic Induction * Learning Outcomes

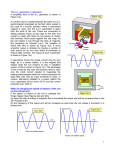
1
Electromagnetic Induction – Learning Outcomes
 Define magnetic flux.
 Solve problems about magnetic flux.
 State Faraday’s Law.
 HL: Solve problems using Faraday’s Law.
 State Lenz’s Law.
 Demonstrate the principles and laws of electromagnetic
induction.
 Discuss electromagnetic induction in generators.
 Solve problems about converting between mechanical and
electrical energy.
2
Electromagnetic Induction
 Just as a current generates a magnetic field, a
changing magnetic field can induce an e.m.f. in a
conductor (usually we consider a coil).
 This effect is called electromagnetic induction.
3
Magnetic Flux
 When a magnetic field of magnetic flux density B passes
perpendicular to an area A, the magnetic flux, Φ
passing through the area is given by:
 𝜙 = 𝐵𝐴
 Magnetic flux is a scalar quantity.
 It is measured in weber, Wb.
 If the magnetic flux density over an area of 1 m2 is 1 T,
then the magnetic flux through the area is 1 Wb.
 Note that if the field passes through a solenoid, the
effective area is proportional to the number of coils.
4
Magnetic Flux
 e.g. What is the magnetic flux through a loop of area 0.4
m2 placed at right angles to a magnetic field of 2 T?
 e.g. The magnetic flux passing though a coil of wire is 2 ×
10-2 Wb. The field is uniform and perpendicular to the
plane of the coil. The area of the coil is 200 cm2. Find the
flux density at any point in the coil.
 e.g. What is the magnetic flux through a loop of area 0.4
m2 in a magnetic field of 2 T if the flux density makes 30o
with the loop?
5
Faraday’s Law
 Faraday’s Law states that the size of the induced emf is
proportional to the rate of change of flux.
 Formula: 𝐸 ∝
Δ𝜙
𝑡
 The constant of proportionality is -1 in this case, so this is
usually written as:
 Formula: 𝐸 =
𝑑𝜙
−
𝑑𝑡
 We can ignore the calculus notation.
 Note the negative sign indicating the direction of the
induced emf (we don’t need it for calculations).
6
Faraday’s Law
 e.g. The magnetic flux through a loop changes from 2
Wb to 8 Wb in 4 seconds. Find the average emf induced
in the loop.
 If the coil has a resistance of 10 Ω, find the induced
current.
 e.g. Find the emf induced in a 100 turn coil of wire if the
flux through it changes from 0 Wb to 6Wb in 0.2 s.
 e.g. A 100 turn rectangular coil of dimensions 6 cm × 8
cm rotates at constant angular speed in a uniform
magnetic field of flux density 2 T. If the coil undergoes 5
rotations per second, find the average induced emf in
the coil in going from parallel to the field to
perpendicular to the field.
7
To Demonstrate Faraday’s Law
1. Connect a coil of wire to a galvanometer.
2. Move a bar magnet slowly towards the coil.
3. Note a small deflection in the galvanometer.
4. Move the bar magnet quickly towards the
coil.
5. Note a larger deflection in the galvanometer.
6. The size of the current (and thus, emf)
increases as the speed of the magnet (and
thus rate of change of flux) increases.
8
Lenz’s Law
 Lenz’s Law states that the direction of an induced
current is always such as to oppose the change
producing it.
 e.g. if a north pole is brought near a solenoid, the
solenoid will produce a current such that its field has a
north pole repulsing the incoming one.
 e.g. if a north pole is moved away from a solenoid, the
solenoid will produce a current such that its field has a
south pole attracting the north pole.
9
Lenz’s Law
 e.g. If the bar magnet is not moving, in which direction
will the current in the solenoid flow?
10
Lenz’s Law
 e.g. If the bar magnet is brought towards the solenoid, in
which direction will the current flow?
11
Lenz’s Law
 e.g. If the bar magnet is moved away from the solenoid,
in which direction will the current flow?
12
To Demonstrate Lenz’s Law
1. Suspend a ring of aluminium from a length of string.
2. Move one pole of a bar magnet quickly towards the
ring.
3. Note that the ring is repelled.
4. Move the magnet quickly away from the ring.
5. Note that the ring is pulled along with the magnet.
6. When the ring is repelled, the induced current creates a
pole the same as the approaching one on that side.
7. When the ring is attracted, the induced current creates
a pole opposite the leaving one on that side.
13
To Demonstrate Lenz’s Law
14
Generators
 An electric generator is a device that converts
mechanical energy to electrical energy.
 Generators use the principles of electromagnetic
induction to perform this conversion.
 In most cases, chemical energy (coal, oil, biomass,
nuclear) is burned for heat, producing steam which
drives a turbine. Wind, hydroelectric, tidal harvest kinetic
energy to drive the turbine.
 Turbines consist of a coil which can rotate in a magnetic
field, inducing an emf.
15
Generators
 Generators appear in:
 Electricity power stations – as described earlier.
 Car alternators – convert rotation in the engine to
electricity to supply the car’s electrical system and
charge the battery.
 Bicycle dynamos harvest the bicycle’s kinetic energy to
operate the lights.
16
Generators
 We examine the simple situation of a magnet moving
towards a coil of wire.
 If the resistance of the coil is 5 Ω and the induced current
is 0.2 A, find the force on the magnet if it moves towards
the coil at 10 m s-1.
 Hint: Conservation
of energy tells us
that the work done
by the magnet is
equal to the heat
produced in the
coil.
17
Generators
 e.g. If the resistance of a coil is 20 Ω and the induced
current is 0.6 A, find the force on the magnet if it moves
towards the coil at 30 m s-1.
 e.g. A rectangular coil of one turn and dimensions 5 cm
× 12 cm enters a uniform magnetic field of flux density 2
T which is perpendicular to the plane of the coil. If the
coil moves at 4 m s-1 parallel to the 12 cm side and has a
resistance of 5 Ω, find:
i.
the emf induced in the coil,
ii.
the force that must be exerted on the coil to keep it
moving at that speed.