Download Basic Statistics for Engineers.

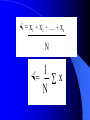
Basic Statistics for Engineers.
Collection, presentation, interpretation
and decision making.
Prof. Dudley S. Finch
Statistics

Four steps:
– Data collection including sampling techniques
– Data presentation
– Data analysis
– Conclusions and decisions based on the
analysis
Data types

Discrete
– Defined as:


A variable consisting of separate values; for example the
number of bolts in a packet. There may be 8 or 9 but there
cannot be 8.5
Continuous
– Defined as:

A variable which may have any value; for example the
diameter of steel bars after machining. Any diameter is
possible within the allowable tolerance to which the machine is
set.
Sampling

Often not practical to examine every component
therefore sampling techniques are used.
 Sample should be representative of the complete
set (the population) of values from which it has
been chosen.
 Although not guaranteed, we attempt to chose an
unbiased sample.
 To be unbiased every possible sample must have
an equal chance of being chosen. Satisfied if
sample is chosen at random; that is, if there is no
order in the way the sample is chosen. This is
called a random sample.
Random samples

The larger the random sample the more
representative of the population it is likely to be.
 Random sampling can be carried out by allocating
a number to each member of the population and
then drawing numbered balls from a bag or using
a random number generator.
 Sampling techniques involve probability theory
(will be dealt with later).
Data presentation
51.4
55.3
56.1
50.5
55.5
52.8
55.6
55.3
50.2
56.1
52.1
54.8
49.6
57.0
52.0
56.5
55.3
54.0
51.6
52.1
57.3
53.9
53.5
56.1
57.2
54.6
55.4
55.9
56.0
52.9
54.1
55.0
54.2
54.2
54.5
53.0
52.7
54.5
54.7
58.4
56.2
55.8
54.1
56.0
55.1
55.1
54.4
57.2
53.2
55.4
53.9
50.9
54.5
56.9
54.0
56.4
53.1
51.8
52.8
50.5
53.7
52.8
54.0
56.4
55.0
53.8
Measured weights of a casting (lbs).
Frequency distribution
The class interval should be one that emphasizes any
pattern in the data. Typically between 8 and 15 class
intervals should be chosen.
In the example used, a class interval of 1lb is chosen.
50lbs therefore includes 49.5 to 50.4lbs. We can therefore
compile a frequency distribution table.
Mass of casting
50
51
52
53
54
55
56
57
58
Number of castings
(frequency)f
2
4
5
8
13
15
12
6
1
Bar chart
16
Frequency (f)
14
12
10
8
6
4
2
0
50
51
52
53
54
55
Variable x (lbs)
56
57
58
Histogram
16
14
Frequency (f)
12
10
8
6
4
2
0
50
51
52
53
54
55
Variable x (lbs)
56
57
58
Frequency polygon
16
Frequency (f)
14
12
10
8
6
4
2
0
50
51
52
53
54
55
Variable x (lbs)
56
57
58
Mass of casting (lbs)
57
.8
56
.9
56
55
.1
54
.2
53
.3
52
.4
51
.5
50
.6
49
.7
Frequency
Frequency curve
7
6
5
4
3
2
1
0
Pie chart showing relative frequency
57
9%
58 50
2% 3%
51
6%
52
8%
56
18%
53
12%
55
22%
54
20%
Relative frequency = class frequency / total frequency of the sample
e.g. the relative frequency of the 53lb class is 8/66 or 0.121
Numerical methods of a
distribution

A frequency distribution can be represented
by two numerical quantities:
– Central tendency or average value of the
distribution
– Dispersion or scatter of variables about the
average value
Numerical measures of central
tendency

Mid point of range:
– Difference between the largest and smallest values of
the variable


Generally poor measure of central tendency since it depends
only on the extreme values of the variable and is not influenced
by the form of the distribution.
Mode:
– The most frequently occurring value of the variable

Easily obtained from frequency table. For the casting the mode
= 55lbs.

Arithmetic mean
– Determined by adding all the values of the
variable and dividing this by the total number
of values. If x1, x2, x3, ….xn are the N values
then…
× = x1 + x2 + ... + xn
¹ ¹ ¹ ¹ N
ˆ
ˆ
1̂
×
x
=
S
¹ ˆˆN
For frequency distribution tables:
mean =
¹ ¹ ¹
f1 x1 + f2 x2 + ... + fn xn
f1 + f2 + ... + fn
where f1 + f2 + ... + fn = N
1
or × =
¹ ¹
N
S fx
To calculate standard deviation:
Evaluate the deviations:
(x1 - ×), (x2 - ×), ... (xn - ×)
Evaluate the squares of the deviations:
2
2
(x1 - ×) , (x2 - ×) , ... (xn - ×)
Evaluate the sum S f(x- ×)
2
2
2
2
= f1 (x1 - ×) , f2 (x2 - ×) , ... fn (xn - ×)
2
Evaluate the average squared deviation
S
f(x- ×)
=
¹ ¹
2
N
Evaluate the standard deviation s

ž 
S f(x- ×)
2
=
¹ ¹ ¹ ˆˆˆN ¹ ¹
¹ ¹ ¹
Estimation

Applies to the difficulty of obtaining data
about the population from which the sample
was drawn and in setting up a mathematical
model to describe this population.
 Two components: estimation and testing of
hypotheses about the chosen model.
Two types of estimates:

Point estimate
– Estimate of a population parameter expressed as a
single number


This method gives no indication as to the accuracy of the
estimate
Interval estimate
– Estimate of a population parameter expressed as two
numbers

This method is preferable as it gives an indication as to where
the population parameter is expected to lie
Confidence intervals
In practice, the true standard deviation, , is
unknown and that the sample standard deviation,
s, is used to estimate .
 If a random sample size n is drawn, an estimate of
the standard error of the sample mean ×is given
by s/ n
 Need to determine the confidence interval for the
true mean, .
 For n>30 a good approximation can be obtained.
For small samples a wider interval is used.


Use of Student t-distribution tables

Look up value for (n-1) and use desired
confidence limits (0.01= 98%, 0.005 = 99%,
0.001 = 99.8%, etc.).
 Find s/ n
 The true mean  = sample mean
 t½,n-1 s/ n


For castings example:
Sample mean = 54.3lbs
Standard deviation, s = 1.83lbs
n = 66
Using t0.005, 65 the true mean  is given by:
54.3  2.66 x 0.225 = 0.599
Thus we can be 99% confident that the true
mean lies between 53.7 and 54.9