Download ME_U1_L5 - Heat and Work

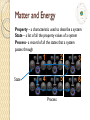
Matter and Energy
Drill
Identify which of the two descriptions of your
class is an intensive property and which is
extensive:


The number of students in the class.
The grade level of the students in class.
Matter and Energy
Now
So
farlet’s
we learn
have how
learned
the state
a bit of
about
a system
systems
can
and howthrough
change
we describe
energythem
transfer.
using properties.
Thermodynamics - study of systems and energy transfer
System – what we choose to study; can be open
or closed
Boundary – separates system from surroundings
Surroundings – everything outside of system
Property – a characteristic used to describe a system
• Extensive – “the whole is the sum of the parts,” Mass,Volume, Energy
• Intensive – “the whole is the same as each part,” Density, Temperature
Matter and Energy
Property – a characteristic used to describe a system
State – a list of all the property values of a system
Process– a record of all the states that a system
passes through
State
1
2
3
4
5
6
Process
Matter and Energy
Thermodynamics - “the study of systems and energy transfer”
Energy can go into or out of a system as either
work or heat …
Energy In
(Weights)
Energy Out
(Ice Bath)
Energy In
(Match)
Piston & Cylinder
Matter and Energy
Thermodynamics - “the study of systems and energy transfer”
Work (W) = a force acting over some distance
Force
Block
Distance
Travelled
If we pushed a block, we would be doing work
on it…
Mechanical Work = Force x Distance = F x d
Matter and Energy
Thermodynamics - “the study of systems and energy transfer”
Mechanical work example:
Block
40 N
d=3m
Remember…only
Mechanical
Work =the
F xcomponent
d
of the force
that is parallel W
to the
= (40
displacement
N)(3 m) does work.
W = 120 N-m
W = 120 J
Matter and Energy
Thermodynamics - “the study of systems and energy transfer”
Mechanical work example:
30O
Mechanical Work = F x d
O
Remember…only
W =the
(40component
N)(Cos 30of
)(3the
m)force
that is parallel W
to the
displacement
does work.
= 103.9
N-m
W ≈ 104 J
Matter and Energy
Thermodynamics - “the study of systems and energy transfer”
Heat (Q) – energy transfer caused by a temperature
difference
•If we place a flame beneath a system, we would
be adding heat to it.
•We could also remove heat by surrounding the
system with an ice bath.
Matter and Energy
Thermodynamics - “the study of systems and energy transfer”
Potential Energy (PE)
Block
Height, h
The block to the right will fall
because a force equal to its mass
times the acceleration of gravity
is acting on it…
PE = mgh
g = 9.8 m/s2
Matter and Energy
Thermodynamics - “the study of systems and energy transfer”
Potential Energy Example:
Block
h=3m
PE = mgh, where g = 9.8 m/s2
PE = (1.5 kg)(9.8 m/s2)(3 m)
PE = 44.1 kg-m2/s2
Remember,
PE
= 44.1 N-m
1 N = kg-m/s2
PE = 44.1 J
m = 1.5 kg
Matter and Energy
Thermodynamics - “the study of systems and energy transfer”
Kinetic Energy (KE)
Block
If the block above moves with a velocity, V, then
its kinetic energy is…
1
2
KE  mV
2
Matter and Energy
Thermodynamics - “the study of systems and energy transfer”
Kinetic Energy Example:
m = 2 kg
V = 5 m/s
Block
If the block above moves with a velocity, V, then
its kinetic energy is…
1
KE  mV 2
2
2
1
1
m
2
KE  (2kg)(5m / s )  (2kg)( 25 2 )  25 J
2
2
s
Matter and Energy
Thermodynamics - “the study of systems and energy transfer”
Expansion or Compression Work
V2
W   PdV
V1
In a constant pressure (isobaric) process,
W  P(V2  V1 )
Matter and Energy
Thermodynamics - “the study of systems and energy transfer”
Expansion Work Example
P = 120 kPa
V2  4 m 3
V1  1.2 m
3
In a constant pressure (isobaric) process,
W  P (V2  V1 )
W  120 kPa(4 m  1.2 m )
W  336 J
3
3