Download MS Word - Sonoma State University

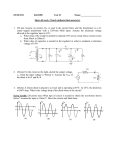
Name ______________________________
ES 330 Electronics II Homework # 1
(Fall 2016 – Due Wednesday, August 31, 2016)
Problem 1 (20 points)
We know that a pn junction diode has an exponential I-V behavior when forward biased.
The diode equation relating current ID and voltage VD is given by (see Section 4.2 of
Sedra & Smith, pp. 184-188)
ID = IS (e(qVD/kT) – 1)
where IS is the saturation current of the diode, VD is the applied voltage across the pn
junction, and kT/q (= VT) is the thermal voltage (kT/q which we will take to equal 26 mV
at so-called “room temperature”).
(a) Using the above expression for ID, find the incremental (i.e., small-signal) resistance
rd under forward bias. You should remember that resistance rd is the derivative
(dVD/dID).
rd =
(b) What is the small-signal diode resistance rd at a forward current of ID = 1
milliampere?
rd = ____ ohms
(c) Suppose the diode is forward biased at a current ID0. How much must one increase
the forward voltage across this diode to increase the current ten-fold in magnitude (that
is, ID1 = 10  ID0 where VD1 = VD0 + ΔVincrease)?
Page
Note: This is sometimes called the “___-millivolt rule” (you fill in the blank with the
value).
1
ΔVincrease = __________ volt
(d) From the expression for diode current, ID = IS (e(qVD/kT) – 1), what does the minus
one term physically represent in the equation for ID?
Problem 2 (18 points)
Continuing with the diode in Problem 1, the saturation current IS = 1  10-15 ampere.
Plot the diode’s forward current ID (on the ordinate) versus the diode’s forward voltage
VD (on the abscissa). For the plot use four different forward voltage values (for
example, you could use VD = 0.5 volt, 0.6 volt, 0.7 volt and 0.8 volt) on the semi-log
graph provided below. Plot your four calculated data points on the graph and then fit a
line to the data.
Page
(b) What is the slope of the curve you plotted (remember this is a semi-log graph)?
2
(a) Plot your four data points on the grid provided below.
(c) Does the “___-millivolt rule” calculated in Problem 1, part (c), also hold true in this
plot? Indicate how this on the plot.
(d) How much does the current increase for a voltage increase of 100 mV?
(e) What is the physical reason for the exponential I-V behavior? (Hint: Think about the
derivation of the diode ID-VD equation covered in ES 230 Electronics I. Remember
when you apply forward bias the potential barrier of the pn junction is lowered.
Therefore, what is the reason this yields an exponential ID-VD characteristic?)
(f) We neglected any to include a parasitic series resistance in the diode (actually, all
physically real fabricated diodes have some parasitic series resistance). How would
you expect the inclusion of this series resistance to change the ID-VD curve on the plot
above? (Note: If you want you can show this effect on the plot.)
Problem 3 (15 points)
In this problem we are presented with an NPN BJT transistor with a saturation current IS
of IS = 8  10-15 ampere and its common-emitter current gain  can vary over the range
of 50 to 200. (Note: This is not uncommon for discrete transistors because
manufacfturers want to sell all the devices they produce.) Suppose you bias the
emitter-base junction at VBE = 0.700 volt, exactly; fiind the values of iC, iB and iE for both
 low = 50 and  high = 200. (Note: Assume kT/q = VT = 0.026 volt in all your calculations)
Parameter
 = 50
 = 200
iC
Page
iE
3
iB
Problem 4 (15 points)
You are presented with an NMOS transistor with a threshold voltage of + 0.5 volt, a
process transconductance parameter nCox = 400 A/V2 and a (W/L) ratio of (5 m/0.4
m). The DC power supplies are plus/minus 1 volt, respectively, and both drain and
source resistors are included.
Design problem: Using the parametric values for the NMOS device given above,
determine the resistance values for RD and RS which meet the criteria of a drain current
ID = 0.1 mA and a drain node voltage VD = + 0.3 volt. (Please show your work.)
RD = _____ ohms
Page
4
RS = _____ ohms
Problem 5 (15 points)
For the NPN BJT in the schematic you can assume infinite current gain (i.e.,  or hFE) .
The two current sources are ideal current sources. If VB is set to zero volts, find the
values of voltages VC and VE at the collector and emitter nodes of the circuit. Clearly
state any assumption you make in doing this problem. (Please show your work.)
VC = ________ volts
VE = ________ volts
Assumption used in work:
_________________________________________
Page
________________________________________________________________
5
________________________________________________________________
The Challenge Problem on Homework #1 (forget Sedra & Smith for
this problem):
Problem 6 (20 points)
A sinusoidal signal generator is used to (a) excite a lumped circuit consisting of
capacitor C shunted by a fifty ohm resistor (upper figure), and (b) excite a distributed
circuit consisting of a three foot length of fifty ohm coaxial cable terminated into a fifty
ohm resistor (lower figure). The coaxial cable is RG 58A/U with a characteristic
impedance of 50 ohms and 32 pF of capacitance per foot length as measured with a 1
MHz capacitance meter. So three feet of RG 58A/U will total 96 pF (= 96  10-12 F).
In the lumped circuit C = 96 pF corresponding to the distributed circuit using three feet
of coax cable. In other words, for both circuits the signal generator is loaded with a 96
pF of capacitor in parallel with 50 ohms. Now we want to compare the frequency
response of the lumped and distributed circuits.
Page
3 dB frequency = ________ MHz
6
(a) For the lumped component circuit, calculate the ratio of output voltage V OUT to input
voltage VS (i.e., VOUT/VS), in other words, calculate the voltage transfer function. What is
the -3 dB response frequency (that is, the frequency for which the response function
falls 3 dB below its low-frequency VOUT/VS magnitude)? Use C = 96 pF and both
resistors are 50 ohms.
Page
7
(b) Next, we now want to compare our result from part (a) with the distributed circuit with
the coaxial transmission line. Ignoring any small resistive losses in the transmission
line, we assume an ideal transmission line (of course, it does have 96 pF of total line
capacitance because it is 3 feet long). If you were to measure the ratio VOUT/VS with
increasing frequency, you would find that VOUT/VS is flat out to extremely high
frequencies (that is, very far beyond the -3 dB cutoff you calculated in part (a)). It turns
out that there is a very important principle at work here. Why do you think the
distributed case has a much higher cutoff frequency than the lumped case?