Download Math 190 Chapter 4 Sample Test – Some Answers (Answers not

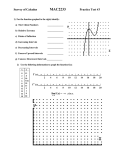
Math 190
Chapter 4 Sample Test – Some Answers
(Answers not guaranteed correct.)
I am not including answers for the problems that were worked in class.
1.
a) Sketch the graph of a continuous function that has two local maxima,
one local minimum and no absolute minimum.
b) Sketch the graph of a function that has three local minima, two local
maxima and seven critical numbers.
Both of these were done in class.
2.
Find the critical numbers of each of these functions
3
2
a) f(x) = x + x + x None
b) g(x) = |3x – 4|
c) h(x) =
3.
x-1
x2 + 4
x=
4
3
x=1+
5
, x=1-
5
Find the absolute maximum and minimum value of these functions on the
intervals indicated.
2
a) f(x) = x e-x
/8
on [-1, 4]
minimum value of –e-1/8 at x = -1
maximum value of 2e-1/2 at x = 2
on [-1,1]
b) f(x) = ln(x2 + x + 1)
minimum value of ln(0.75) at x = -0.5
maximum value of ln3 at x = 1
4.
a) Show that 5 is a critical number of the function f(x) = 2 + (x – 5)3 but
f does not have a local extreme value at 5.
b) Show that the function f(x) = x101 + x51 + x + 1 has neither a local
maximum nor a local minimum.
This problem was done in class. Note that 4a) originally contained a
typographic error.
5.
a) Show that the equation 2x – 1 – sinx = 0 has exactly one real root.
Hints: Let f(x) = 2x – 1 – sinx. Note that f(0) = -1 < 0 and f(π) = 2π -1 >
0. Since f(x) is continuous it must cross the x-axis and have at least one
real root between x = 0 and x = π. Also note that f’(x) >0, so f(x) is
always increasing. Do something with that.
b) Show that the equation x4 + 4x + c = 0 has at most two real roots.
Hints: Note that f’(x) = 0 only at x = -1 and that f’’(x) > 0. Do something
with that.
6. & 7.
For each of the following functions find:
a)
b)
c)
the intervals on which f is increasing or decreasing,
the local maximum and minimum values of f,
the intervals of concavity and the inflections points.
6.
a)
b)
c)
f(x) = 4x3 + 3x2 – 6x + 1
increasing on (-∞, -1) ⋃ (1/2, ∞) , decreasing on (-1, ½)
local max: (-1,6) , local min: (1/2 , -3/4 )
CC↑ (-1/4, ∞), CC↓ (-∞, -1/4), infl. point (-1/4, -3/8)
7.
f(x) = x2 lnx Done in class.
8.
Use Newton’s method to find all roots of this equation correct to six
decimal places. ex = 3 – 2x
Hint: Draw a graph of y = e and a graph of y = -2x + 3 and notice that
they intersect at a value of x less than 1.5, so start off by guessing x1 = 1.
It should not take too many steps to get that x ≈ 0.594205. (I also tried
starting with x = .8 and it took me more steps than starting at x = 1 did.)
9.
Find an equation of the line through the point (3, 5) that cuts off the least
area from the first quadrant. Done in class. (Actually, I’m not sure I
finished the problem and found the equation of the line, rather than what
the minimum area is.)
10. A woman at a point A on the shore of a circular lake of radius 2 miles want
to arrive at the point C diametrically opposite point A on the other side of
the lake in the shortest possible time. She can walk at the rate of 4 mi/hr
and row a boat at 2 mi/hr. How should she proceed? Done in class.
11. Find these limits.
lim+ (sinx lnx) = 0
a)
x→0
b)
lim+ (tan2x)x
x→0
=1
12. Let f(t) be the temperature at time t where you live and suppose that at
time t = 3 you feel uncomfortably hot. How do you feel about the given
data in each case? Explain. Done in class.
a) f’(3) = 2, f’’(3) = 4
b)
f’(3) = 2, f’’(3) = -4
c) f’(3) = -2, f’’(3) = 4
d)
f’(3) = -2, f’’(3) = -4
13. For this function: y = 200 + 8x3 + x4 , find:
a) the intervals of increase or decrease,
increase: (-6,0) ⋃ (0,8) decrease: (-∞, -6)
b) the local maximum and minimum values,
minimum value of y = -232 at x = -6.
c) the intervals of concavity and the inflection points,
CC↑ (-∞,-4) ⋃ (0, ∞), CC↓ (-4,0), inflection points: (-4, -56) and (0, 200).
and then
d) use this information to sketch the curve. Sorry, no time to scan this.
14. For this function: y = ln(x4 + 27) , find:
a) the intervals of increase or decrease,
decrease: (-∞, 0), increase: (0, ∞)
b) the local maximum and minimum values,
local minimum value of y = ln27 at x = 0.
c) the intervals of concavity and the inflections points,
CC↑  -3
 2
;
3
2


CC↓ -∞;
inflection points: 

-3
2
3
189
;
4 
2
 ⋃  3 ; ∞ ,
 2


and 

-3 189
;
4 
2
and then
d) use this information to sketch the curve. Sorry, no time to scan this.
15. Sketch the graph of a continuous function that satisfies all of the given
conditions: Done in class.
g’(1) = g’(-1) = 0
g’(x) = -1 if |x| > 2,
g’(x) < 0 if |x| <1,
g’(x) > 0 if 1 < |x| < 2,
g’’(x) < 0 if -2 < x < 0, inflection point (0,1)