Survey
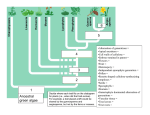
* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download 1 - bioRxiv
Document related concepts
Viral phylodynamics wikipedia , lookup
Polymorphism (biology) wikipedia , lookup
Species distribution wikipedia , lookup
Group selection wikipedia , lookup
Heritability of IQ wikipedia , lookup
Koinophilia wikipedia , lookup
Genetic drift wikipedia , lookup
Quantitative trait locus wikipedia , lookup
Transcript
