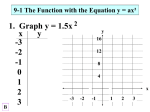
* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Parabolas Project Example
Survey
Document related concepts
Transcript
StudentP 1April2017 QuadraticFunctionsPerformanceTask Period4 Algebra1 Debel ParabolasintheRealWorld Parabolascanbefoundeverywhereinourday-to-daylives.Theyexistinarchitecture,art, objects,andthepathsofprojectiles.HerearesomeexamplesIfound: Theenormoussteelcablessupportingthefamous GoldenGateBridgeinSanFranciscoforma parabolathatopensupwards.Thedistance betweenthetowersofthebridgeis1,200meters! Thetopsofthetowersrearabout230metersabove sealevel.Eachofthetwomaincablessuspending thebridgeis2332meterslongs. (source:goldengatebridge.org) Justabouteveryobjectthatisthrownintotheair followsaparabolicpath.Thisappliestofootballs, bullets,cannonballs,arrows,Frisbees,androcks. (Somelightobjects,suchasballoonsorpaper airplanes,willnotfollowaparabolicpath,butwill bemovedaboutbytheair.)Someobjectswhich areveryfast,suchasbullets,willhaveaverywide parabolicpath(verticalcompression).Iwatched childrenthrowingballsthatfollowedparabolic paths,butwasn’tabletocapturethisinastill picture. ThislittleTiffany-stylelampsitsinmylivingroom atopthepiano.Itslampshadeisapproximately parabolic.(Ofcoursethelampshadeisthree dimensional,butitcrosssectionisaparabola.) Thevertexoftheparabolaisatthetopofthe lampshade.Thislittleparabolaisonlyaboutfive inchestall. StudentP QuadraticFunctionsPerformanceTask Algebra1 Debel TheEiffelTowerinParis, France,isaremarkable featofarchitecture,full offascinatinggeometry. Itslowerarchesare roughlyparabolicin shape.Thedimensionsin mymodelareinmeters, andapproximatethetrue measurementsofthe EiffelTower. Ihavealignedthe x-axiswiththe groundandthe y-axiswiththe axisofsymmetry oftheparabola. 1April2017 Period4 Vertexandy-intercept: (#, &#) Maximum:50 Axisofsymmetry: ! = # x-intercept (−)*, #) x-intercept ()*, #) StudentP 1April2017 QuadraticFunctionsPerformanceTask Period4 Algebra1 Debel Ihavealignedmyx-axiswiththeground.They-axisgoesthroughthecenterofthe towerandismyaxisofsymmetry. Allmeasurementsareapproximateandareinmeters. Thezeros(x-intercepts)oftheparabolaarethepointsatwhichtheinsideedgesof thetower’ssupportstouchtheground. Thecoordinatesofthezerosareat: (−37,0)/01(37,0) TheVertexoftheparabolaisat: (0,50) They-interceptisalsothevertexandisat: (0,50) Theaxisofsymmetryisthey-axis.Itsequationis: 3 = 0 Themaximumvalueoftheparabolaistheheightofthearch: 50 TableofValues: X Y (Ireadthesevalues -37 0 offmygraph.Iusedthe -10 46 pointsontheparabola,even 0 50 thoughtheywereslightly 25 27 differentfromthepointson 37 0 theEiffelTower.) StudentP 1April2017 QuadraticFunctionsPerformanceTask Period4 Algebra1 Debel FindingtheEquationofmyParabola: Tofindtheequationofmyparabolainfactoredform,Ifirstpluginthezeros(-37and37)for “p”and“q:” 4 3 =/ 3−5 3 =6 4 3 = /(3 + 37)(3 − 37) Ithenpluginthevertexforxandyinordertofindthevalueofa: 50 = / 0 + 37 0 − 37 50 = / ∙ −1369 50 /=− 1369 FromthisIcanassemblemyfunction: < ! =- &# (! + )*)(!-)*) >)?@ Icanconvertmyfunctiontogeneral/standardformbyapplyingFOILandsimplifyingtheresult: 50 4 3 =− (3 A − 373 + 373 − 1369) 1369 50 4 3 =− (3 A − 1369) 1369 < ! =- &# B ! + &# >)?@ FindingVertexFormisveryeasyinthiscase!Thatisbecauseinthiscase,generalformand vertexformareidentical.Icouldexpressmyfunctioninthefollowingwaytomakevertexform evenmorerecognizable: < ! = &# !-# >)?@ B + &# CℎEFGH/0FIℎHJHKIH3EF/I(0,50) StudentP 1April2017 QuadraticFunctionsPerformanceTask Period4 Algebra1 Debel Iwillnowpluginoneofthepointsfrommytableofvalues(25,27)toverifywhethermy functionisworking.Iwilltryallthreeforms.(Iwilluseacalculatortohelpwithmymath!) FactoredForm: 50 4 25 = − 25 + 37 25 − 37 1369 50 4 25 = − ∙ 62 ∙ (−12) 1369 4 25 = 27.17 GeneralForm/VertexForm: 50 4 25 = − (25)A + 50 1369 50 4 25 = − ∙ 625 + 50 1369 31250 4 25 = − + 50 1369 4 25 = 27.17 ThepointIreadoffofmygraphwasat(25,27).ThisisveryclosetothevaluesIcalculatedwith myfunctions!(Theonlydifferenceisthelevelofaccuracy.Graphspermitonlyan approximationofvalues,whilethefunctionwillprovideamoreaccuratevalue.) IndoingthisprojectIlearnedthatparabolasoccurineverydaylife,andthatIhavethetoolsto graphthemandwritefunctionstodescribeandmakecalculationsaboutthem.Therearemany potentialapplicationsforthisskill,suchaspredictingwhereathrownobjectmayland, calculatingtheheightofanarchthatistootallformetomeasuredirectly,ordescribingthe preciseshapeIwouldlikeafancywindowtohaveinabuildingImaydesignoneday. I’vestartedseeingparabolaseverywhere:Evensomeheadsareparabolic!