ellipse - einstein classes
... Major Axis : The line segment AA in which the focii S and S lie (of length 2a) is called the major axis of the ellipse. Point of intersection of major axis with directrix is called the foot of the directrix (z and z ). Minor Axis : The y-axis intersects the ellipse in the points B (0, b ) and ...
... Major Axis : The line segment AA in which the focii S and S lie (of length 2a) is called the major axis of the ellipse. Point of intersection of major axis with directrix is called the foot of the directrix (z and z ). Minor Axis : The y-axis intersects the ellipse in the points B (0, b ) and ...
classwork geometry 5/13/2012
... in the figure, for any P’ on l the distance to l’, |P’L’| ≤ |P’L| ≤ |P’F| + |FL|, where |FL| is the distance from F to l’. Hence, |P’L’| - |P’F| ≤ |FL| and the difference is largest (=|FL|) when point P belongs to the perpendicular FL from point F to l’. The optical property of the hyperbola. Suppos ...
... in the figure, for any P’ on l the distance to l’, |P’L’| ≤ |P’L| ≤ |P’F| + |FL|, where |FL| is the distance from F to l’. Hence, |P’L’| - |P’F| ≤ |FL| and the difference is largest (=|FL|) when point P belongs to the perpendicular FL from point F to l’. The optical property of the hyperbola. Suppos ...
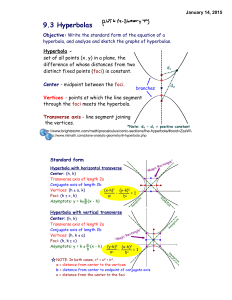
9.3 Hyperbolas
... http://www.brightstorm.com/math/precalculus/conic-sections/the-hyperbola/#ooid=ZzaWV3NDoSM36UvSLAMq-B http://www.intmath.com/plane-analytic-geometry/6-hyperbola.php ...
... http://www.brightstorm.com/math/precalculus/conic-sections/the-hyperbola/#ooid=ZzaWV3NDoSM36UvSLAMq-B http://www.intmath.com/plane-analytic-geometry/6-hyperbola.php ...
Unit 6 - Katey Parham
... In general, if the distance from the vertex to the focus (or directrix) is c and the vertex is (h, k), the equation in information form is ...
... In general, if the distance from the vertex to the focus (or directrix) is c and the vertex is (h, k), the equation in information form is ...
Math 11 Final Fall 2010
... 1. Find the slope-intercept equation of the line that contains the points (3,2) and (5,18) and prove that the point (10,28) is also on this line. ...
... 1. Find the slope-intercept equation of the line that contains the points (3,2) and (5,18) and prove that the point (10,28) is also on this line. ...
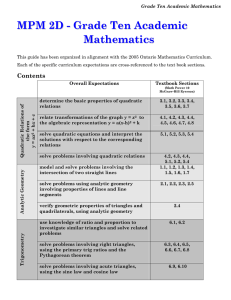
MPM 2D - Grade Ten Academic Mathematics
... y = a(x-h)2 + k Students will learn about each of the components in the above standard form of a quadratic and what impact they will have on the graph of y = x2 from a transformation point of view. a : the vertical stretch/compression factor and vertical reflection component if a > 1, then parabola ...
... y = a(x-h)2 + k Students will learn about each of the components in the above standard form of a quadratic and what impact they will have on the graph of y = x2 from a transformation point of view. a : the vertical stretch/compression factor and vertical reflection component if a > 1, then parabola ...
HighSchoolMath_revie..
... Since the parabola opens downward, we know that To find the value of a, you also need to know another point on the parabola. Since we know the parabola passes through the point ...
... Since the parabola opens downward, we know that To find the value of a, you also need to know another point on the parabola. Since we know the parabola passes through the point ...
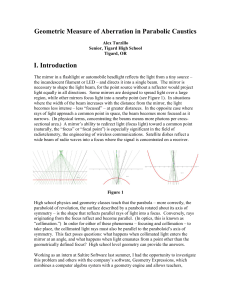
Geometric Measure of Aberration in Parabolic Caustics
... For a given angle of incoming light (), we observe that rays that intersect the parabola near the vertex make reflections that intersect each other near the bottleneck (Figure 3); while rays that intersect the parabola farther from the vertex make reflections that intersect each other farther from ...
... For a given angle of incoming light (), we observe that rays that intersect the parabola near the vertex make reflections that intersect each other near the bottleneck (Figure 3); while rays that intersect the parabola farther from the vertex make reflections that intersect each other farther from ...
Quiz 8 Review Blank
... ____ T9 (A1): Use coordinates to prove simple geometric theorems algebraically. For example, prove or disprove that a figure defined by four given points in the coordinate plane is a rectangle; prove or disprove that the point (1, √3) lies on the circle centered at the origin and containing the poin ...
... ____ T9 (A1): Use coordinates to prove simple geometric theorems algebraically. For example, prove or disprove that a figure defined by four given points in the coordinate plane is a rectangle; prove or disprove that the point (1, √3) lies on the circle centered at the origin and containing the poin ...
Solution of Sondow`s problem: a synthetic proof of the tangency
... The tangent line of a parabola at either endpoint of its latus rectum forms an angle of π4 with the latus rectum. As such, parabolas G1 and G2 share the same tangent at C1 , and similarly parabolas G2 and G3 share a tangent at C3 . At cusp C2 , however, we obtain two different tangent directions. On ...
... The tangent line of a parabola at either endpoint of its latus rectum forms an angle of π4 with the latus rectum. As such, parabolas G1 and G2 share the same tangent at C1 , and similarly parabolas G2 and G3 share a tangent at C3 . At cusp C2 , however, we obtain two different tangent directions. On ...
Supplementary Information
... Joel D. Leger,1,a) Clara M. Nyby,1,a) Clyde Varner,1 Jianan Tang,1 Natalia I. Rubtsova,1 Yuankai Yue,1 Victor V. Kireev,1 Viacheslav D. Burtsev,1 Layla N. Qasim,1 Grigory I. Rubtsov,2 and Igor V. Rubtsov1,* ...
... Joel D. Leger,1,a) Clara M. Nyby,1,a) Clyde Varner,1 Jianan Tang,1 Natalia I. Rubtsova,1 Yuankai Yue,1 Victor V. Kireev,1 Viacheslav D. Burtsev,1 Layla N. Qasim,1 Grigory I. Rubtsov,2 and Igor V. Rubtsov1,* ...
LOYOLA COLLEGE (AUTONOMOUS), CHENNAI – 600 034
... 8. Define conjugate diameters of an ellipse. 9. Define rectangular hyperbola. 10. Define polar equation of a conic. PART – B Answer any FIVE questions: ...
... 8. Define conjugate diameters of an ellipse. 9. Define rectangular hyperbola. 10. Define polar equation of a conic. PART – B Answer any FIVE questions: ...
Getting Started with Precalculus Equations of Parabolas
... Students work with parabolas whose vertex is on the origin as well as off the origin and they work with parabolas that open not only up and down, but also to the left and to the right. For these, they graph the parabola by writing two functions. Students will derive general equation for parabolas, f ...
... Students work with parabolas whose vertex is on the origin as well as off the origin and they work with parabolas that open not only up and down, but also to the left and to the right. For these, they graph the parabola by writing two functions. Students will derive general equation for parabolas, f ...
DEFINITIONS and GLOSSARY • Graph paper: paper
... Parabola: the set of all points in a plane which are equidistant from a fixed point F, called the focus, and a fixed line d (not containing F), called the directrix. Axis of symmetry of a parabola: the line through the vertex perpendicular to the directrix quadratic equation: ax2 + bx + c = 0 to sol ...
... Parabola: the set of all points in a plane which are equidistant from a fixed point F, called the focus, and a fixed line d (not containing F), called the directrix. Axis of symmetry of a parabola: the line through the vertex perpendicular to the directrix quadratic equation: ax2 + bx + c = 0 to sol ...
Activities - WVU Math Department
... 5. Go to the second function in the drop down menu, a parabola. Find the area when a=0 and b=4. Find the area when a=-4 and b=4. (The E-14 indicates exponential notation, so the value in the second window is essentially 0). What property of the parabola accounts for the reported area when a=-4 and b ...
... 5. Go to the second function in the drop down menu, a parabola. Find the area when a=0 and b=4. Find the area when a=-4 and b=4. (The E-14 indicates exponential notation, so the value in the second window is essentially 0). What property of the parabola accounts for the reported area when a=-4 and b ...
Parabolas Project Example
... Finding Vertex Form is very easy in this case! That is because in this case, general form and vertex form are identical. I could express my function in the following way to make vertex form even more recognizable: ...
... Finding Vertex Form is very easy in this case! That is because in this case, general form and vertex form are identical. I could express my function in the following way to make vertex form even more recognizable: ...
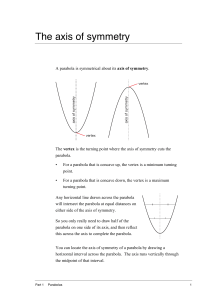
The axis of symmetry
... The axis runs through the midpoint of (0, 8) and (4, 8). You can easily see this point to be (2, 8). (You don’t need to use the midpoint formula for this.) The equation for the axis of symmetry is x = 2 . ...
... The axis runs through the midpoint of (0, 8) and (4, 8). You can easily see this point to be (2, 8). (You don’t need to use the midpoint formula for this.) The equation for the axis of symmetry is x = 2 . ...
Tangents to Curves
... our straightedge to draw a unique straight line that passes through both of the points • Given any fixed point in the plane, and any fixed distance, we can use our compass to draw a unique circle having the point as its center and the distance as its radius ...
... our straightedge to draw a unique straight line that passes through both of the points • Given any fixed point in the plane, and any fixed distance, we can use our compass to draw a unique circle having the point as its center and the distance as its radius ...
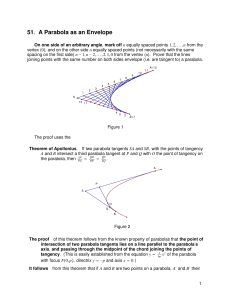
51. A Parabola as an Envelope
... intersection of two parabola tangents lies on a line parallel to the parabola’s axis, and passing through the midpoint of the chord joining the points of tangency. (This is easily established from the equation y 4p1 x 2 of the parabola with focus F0, p , directrix y "p and axis x 0. ) It fol ...
... intersection of two parabola tangents lies on a line parallel to the parabola’s axis, and passing through the midpoint of the chord joining the points of tangency. (This is easily established from the equation y 4p1 x 2 of the parabola with focus F0, p , directrix y "p and axis x 0. ) It fol ...