Download The Rotational Hamiltonian

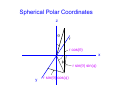
Chemistry 431
Lecture 6
Rotational motion
NC State University
Classical Rotation
In a circular trajectory Jz = pr and E = Jz2/2I.
I is the moment of inertia.
Diatomic I = μr2
Mass in a circle I = mr2.
r
m
r
m1
m2
m 1m 2
μ
=
Reduced mass
m1 + m2
Rotation in two dimensions
The angular momentum is Jz = pr.
Jz
r
m
p
Using the deBroglie relation p = h/λ we also
have a condition for quantization of angular
motion Jz = hr/λ.
The 2-D rotational hamiltonian
• The wavelength must be a whole number
fraction of the circumference for the ends to
match after each circuit.
• The condition 2πr/m = λ combined with the
deBroglie relation leads to a quantized
expression,Jz = mh.
2 2
• The hamiltonian is: – h ∂ Φ2 = EΦ
2I ∂φ
The 2-D rotational hamiltonian
• Solutions of the 2-D rotational hamiltonian are
sine and cosine functions just like the particle in
a box.
• Here the boundary condition is imposed by the
circle and the fact that the wavefunction must not
interfere with itself.
• The 2-D model is similar to condition in the Bohr
model of the atom.
The 2-D rotational hamiltonian
• The wavelength must be a whole number
fraction of the circumference for the ends to
match after each circuit.
• The condition 2πr/m = λ combined with the
deBroglie relation leads to a quantized
expression,Jz = mh.
2 2
h ∂Φ
• The hamiltonian is:
–
2I ∂φ
2
= EΦ
Quantization of rotational motion:
solution of the φ equation
The corresponding wavefunctions are:
1
Φm=
2π
1/2
with the constraint that:
2IE
m=±
h
e
imφ
1/2
Since the energy is constrained to values Jz2/2I we find that
m = 0, ±1, ± 2, ...
The wavefunctions of a rigid rotor are
called spherical harmonics
The solutions to the θ and φ equation (angular part)
are the spherical harmonics Y(θ,φ )= Θ(θ)Φ(φ)
Separation of variables using the functions Θ(θ)
and Φ(φ) allows solution of the rotational wave
equation.
2
h
∂
Y
1 ∂ sinθ ∂Y
1
–
+
∂θ
2I sin 2θ ∂ϕ 2 sinθ ∂θ
2
= EY
We can obtain a θ and φ equation from the above
equation.
Spherical Polar Coordinates
z
θ
r
r cos(θ)
x
φ
r sin(θ) sin(φ)
y
r sin(θ) cos(φ)
The volume element in spherical
polar coordinates
To solve the Schrodinger equation we need to
integrate of all space. This is the same thing
as performing a volume integral. The volume
element is:
dV = r 2dr sinθdθ dφ
This integrates to 4π, which is the
normalization constant. 4π stearadians also
gives the solid angle of a sphere.
Separation of variables
The spherical harmonics arise from the product
of ΘΦ after substituting Y = ΘΦ
∂ 2ΦΘ + sinθ ∂ sinθ ∂ΦΘ = sin 2θEΦΘ
∂θ
∂θ
∂ϕ 2
For sake of simplicity, we have factored the term
2
h
–
2I
into the energy. At the end of the calculation we
Will multiply by this term to obtain the energy.
Separation of variables
The operators in variables θ and φ operate on functio
Θ and Φ , respectively, so we can write
2
Θ ∂ Φ2 + Φsinθ ∂ sinθ ∂Θ = sin θEΦΘ
∂θ
∂θ
∂ϕ
2
When we divide by Y = ΘΦ, we obtain
2
∂
1 Φ + 1 sinθ ∂ sinθ ∂Θ – sin 2θE = 0
Φ ∂ϕ 2 Θ
∂θ
∂θ
Now, these equations can be separated.
Separation of variables
We use a separation constant equal to m2 to write
two equations. The θ and φ equations are
sinθ ∂ sinθ ∂Θ
Θ ∂θ
∂θ
2
1 ∂Φ
Φ ∂φ 2
– sin θE = m 2
2
= – m2
We have already seen the solution to the φ equation
from the example of rotation in two dimensions.
The solution of θ equation gives
Legendre polynomials
Substitute x = cosθ and the equation becomes:
2
∂
P
m
∂P
1–x
– 2x
+ E–
P=0
2
2
∂x
1–x
∂x
2
2
The solution requires that Ε=-(h2/2I)J(J+1) with J=0,1,2
Where J is the rotational quantum number.
The azimuthal quantum number m is also called Jz.
The magnitude of |Jz|<J. The solutions are Legendre
polynomials
P0(x)=1
P2(x)=1/2 (3x2 - 1)
P1(x)=x
P3(x)=1/2 (5x3 - 3x)
The spherical harmonics as solutions to
the rotational hamiltonian
The spherical harmonics are the product of the
solutions to the θ and φ equations. With norm-alization these solutions are
Y (θ,φ) = NJMP (cos θ)e
M
J
|M|
J
iMφ
The M quantum number corresponds to Jz the
z component of angular momentum. The norm-alization constant is
NJM
(J – |M|)!
2J
+
1
=
2 (J + |M|)!
1/2
The form of the spherical
harmonics
Including normalization the spherical harmonics are
Y00 = 1
4π
0
3 cosθ
Y1 = 4π
±1
Y1
=
0
Y2 =
±1
2
Y =
3 sinθe ±iφ 2
Y2 =
8π
5 3cos 2θ – 1
16π
15 sinθcosθe ±iφ
8π
15 sin 2θe ±2iφ
32π
The form commonly used to represent p and d
orbitals are linear combinations of these functions
Euler relation
Linear combinations are formed using the Euler relatio
e ±iφ = cosθ ± isinθ
iφ
–iφ
sinθ = e – e
2i
iφ
–iφ
+
e
e
cosθ =
2
Projection along the z-axis is usually taken using
z = rcosθ. Projection in the x,y plane is taken using
x = rsinθcosφ and y = rsinθsinφ
The 3-D rotational hamiltonian
• There are two quantum numbers
J is the total angular momentum quantum number
M is the z-component of the angular momentum
• The spherical harmonics called YJM are functions whose
probability |YJM|2 has the well known shape of the s, p
and d orbitals etc.
• J = 0 is s , M = 0
• J = 1 is p , M = -1, 0 , 1
• J = 2 is d , M = -2 , -1, 0 , 1, 2
Space quantization in 3D
• Solutions of the rotational
Schrödinger equation have
z
M = +2
M = +1
M=0
M = -1
M = -2
J=2
energies E = h2 J(J +1)/2I
• Specification of the azimuthal
quantum number mz implies
that the angular momentum
about the z-axis is Jz = hmz.
• This implies a fixed orientation
between the total angular
momentum and the z
component.
• The x and y components
cannot be known due to the
Uncertainty principle.
Spherical harmonic for
P0(cosθ)
• Plot in polar coordinates
represents |Y00|2 where
Y00=(1/4π)1/2 .
• Solution corresponds to
rotational quantum numbers
J = 0,
• M or Jz = 0.
• Polynomial is valid for n≥1
quantum numbers of
hydrogen wavefunctions
Spherical harmonic for
P1(cosθ)
• Plot in polar coordinates
represents |Y11|2 where
Y11=(1/2)(3/2π)1/2 sinθeiφ.
• Solution corresponds to
rotational quantum
numbers J = 1, Jz = ±1.
• Polynomial is valid for
n≥2 quantum numbers of
hydrogen wavefunctions
Spherical harmonic for
P1(cosθ)
• Plot in polar coordinates
represents |Y10|2 where
Y10=(1/2)(3/π)1/2 cosθ
with normalization.
• Solution corresponds to
rotational quantum
numbers J = 1, Jz = 0.
• Polynomial is valid for
n≥2 quantum numbers of
hydrogen wavefunctions.
Spherical harmonic for
P2(cosθ)
• Plot in polar coordinates
of |Y22|2 where
Y22=1/4(15/2π)1/2cos2θe2iφ
• Solution corresponds to
rotational quantum
numbers J = 2, Jz = ± 2.
• Polynomial is valid for
n≥3 quantum numbers of
hydrogen wavefunctions
Spherical harmonic for
P2(cosθ)
• Plot in polar coordinates
of |Y21|2 where
Y21=(15/8π)1/2sinθcosθeiφ
• Solution corresponds to
rotational quantum
numbers J = 2, Jz = ± 1.
• Polynomial is valid for
n≥3 quantum numbers of
hydrogen wavefunctions
Spherical harmonic for
P2(cosθ)
• Plot in polar coordinates
of |Y20|2 where
Y20=1/4(5/π)1/2(3cos2θ-1)
• Solution corresponds to
rotational quantum
numbers J = 1, Jz = 0.
• Polynomial is valid for
n≥3 quantum numbers of
hydrogen wavefunctions
Rotational Wavefunctions
J=0
J=1
J=2
These are the spherical harmonics YJM, which
are solutions of the angular Schrodinger equation.
The degeneracy of the
solutions
• The solutions form a set of 2J + 1 functions at each
energy (the energies are E = h2 J(J +1)/2I.
• A set of levels that are equal in energy is called a
degenerate set.
J=3
J=2
J=1
J=0
Rotational Transitions
• Electromagnetic radiation can interact with a molecule to
change the rotational state.
• Typical rotational transitions occur in the microwave
region of the electromagnetic spectrum.
• There is a selection rule that states that the quantum
number can change only by + or - 1 for an allowed
rotational transition (ΔJ = ±1).
J=2
J=1
J=0
Orthogonality of
wavefunctions
• The rotational wavefunctions can be represented as the
product of sines and cosines.
• Ignoring normalization we have:
• s 1
• p cosθ sinθcosφ sinθsinφ
• d 1/2(3cos2θ - 1), cos2θcos2φ , cos2θsin2φ ,
cosθsinθcosφ , cosθsinθsinφ
• The differential angular element is sinθdθdφ/4π over
• the limits θ = 0 to π and φ = 0 to 2π.
• The angular wavefunctions are orthogonal.
Orthogonality of
wavefunctions
• For the theta integrals we can use the substitution
• x = cosθ and dx = sinθdθ
• For example, for s and p-type rotational wave functions we
have
π
<s|p>∝
–1
cosθ sinθ dθ =
0
1
2
x
x dx =
2
–1
1
= 1 – 1 =0
2 2
Question
Which of the following statements is true:
A. The number of z-projection of the quantum numbers is
2J+1.
B. The spacing between rotational energy levels increases
as 2(J+1).
C. Rotational energy levels have a degeneracy of 2J+1.
D. All of the above.
Question
Which of the following statements is true:
A. The number of z-projection of the quantum numbers is
2J+1.
B. The spacing between rotational energy levels increases
as 2(J+1).
C. Rotational energy levels have a degeneracy of 2J+1.
D. All of the above.
ΔE ~ (J +2)(J + 1) – J(J + 1) = 2(J + 1)
Question
The fact that rotational wave functions are orthogonal means
that
A. They have no overlap
B. They are normalized
C. They are linear functions
D. None of the above
Question
The fact that rotational wave functions are orthogonal means
that
A. They have no overlap
B. They are normalized
C. They are linear functions
D. None of the above
The moment of inertia
The kinetic energy of a rotating body is 1/2Iω2.
The moment of inertia is given by:
∞
I=
Σ mr
i=1
2
i i
The rigid rotor approximation assumes that
molecules do not distort under rotation. The types
or rotor are (with moments Ia , Ib , Ic)
- Spherical: Three equal moments (CH4, SF6)
(Note: No dipole moment)
- Symmetric: Two equal moments (NH3, CH3CN)
- Linear: One moment (CO2, HCl, HCN)
(Note: Dipole moment depends on asymmetry)
- Asymmetric: Three unequal moments (H2O)
The rotational partition function
The degeneracy of rotational levels is J(J+1).
The energies are given by ε = hcBJ(J+1) where
J is the rotational quantum number and B is the
rotational constant.
∞
qr =
Σ
J=0
(2J + 1)e
– βhcBJ(J + 1)
A large number of rotational levels populated since
the rotational constant is of the order of 10 cm -1 for
many molecules and kT > 10 cm-1 for temperatures
higher than about 15 K.
The high temperature form of the
rotational partition function
The partition function can be expressed as an
integral at high temperature.
∞
qr =
(2J + 1)e – βhcBJ(J + 1)dJ
0
It turns out that the integral can be solved
analytically by making the substitution u = J(J+1).
u = J(J + 1), du = (2J + 1)dJ
The rotational partition function
is an exponential integral
Making the substitution u = J(J+1) the integral
reduces to an easily soluble exponential integral.
∞
qr =
e
0
– βhcBu
1
du =
βhcB
The rotational constant B is:
B=
h where I is the moment of inertia
4πcI