* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download The Rotational Hamiltonian
Atomic orbital wikipedia , lookup
Franck–Condon principle wikipedia , lookup
Heat transfer physics wikipedia , lookup
Eigenstate thermalization hypothesis wikipedia , lookup
Rigid rotor wikipedia , lookup
Relativistic quantum mechanics wikipedia , lookup
Molecular Hamiltonian wikipedia , lookup
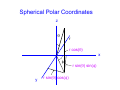
Chemistry 431 Lecture 6 Rotational motion NC State University Classical Rotation In a circular trajectory Jz = pr and E = Jz2/2I. I is the moment of inertia. Diatomic I = μr2 Mass in a circle I = mr2. r m r m1 m2 m 1m 2 μ = Reduced mass m1 + m2 Rotation in two dimensions The angular momentum is Jz = pr. Jz r m p Using the deBroglie relation p = h/λ we also have a condition for quantization of angular motion Jz = hr/λ. The 2-D rotational hamiltonian • The wavelength must be a whole number fraction of the circumference for the ends to match after each circuit. • The condition 2πr/m = λ combined with the deBroglie relation leads to a quantized expression,Jz = mh. 2 2 • The hamiltonian is: – h ∂ Φ2 = EΦ 2I ∂φ The 2-D rotational hamiltonian • Solutions of the 2-D rotational hamiltonian are sine and cosine functions just like the particle in a box. • Here the boundary condition is imposed by the circle and the fact that the wavefunction must not interfere with itself. • The 2-D model is similar to condition in the Bohr model of the atom. The 2-D rotational hamiltonian • The wavelength must be a whole number fraction of the circumference for the ends to match after each circuit. • The condition 2πr/m = λ combined with the deBroglie relation leads to a quantized expression,Jz = mh. 2 2 h ∂Φ • The hamiltonian is: – 2I ∂φ 2 = EΦ Quantization of rotational motion: solution of the φ equation The corresponding wavefunctions are: 1 Φm= 2π 1/2 with the constraint that: 2IE m=± h e imφ 1/2 Since the energy is constrained to values Jz2/2I we find that m = 0, ±1, ± 2, ... The wavefunctions of a rigid rotor are called spherical harmonics The solutions to the θ and φ equation (angular part) are the spherical harmonics Y(θ,φ )= Θ(θ)Φ(φ) Separation of variables using the functions Θ(θ) and Φ(φ) allows solution of the rotational wave equation. 2 h ∂ Y 1 ∂ sinθ ∂Y 1 – + ∂θ 2I sin 2θ ∂ϕ 2 sinθ ∂θ 2 = EY We can obtain a θ and φ equation from the above equation. Spherical Polar Coordinates z θ r r cos(θ) x φ r sin(θ) sin(φ) y r sin(θ) cos(φ) The volume element in spherical polar coordinates To solve the Schrodinger equation we need to integrate of all space. This is the same thing as performing a volume integral. The volume element is: dV = r 2dr sinθdθ dφ This integrates to 4π, which is the normalization constant. 4π stearadians also gives the solid angle of a sphere. Separation of variables The spherical harmonics arise from the product of ΘΦ after substituting Y = ΘΦ ∂ 2ΦΘ + sinθ ∂ sinθ ∂ΦΘ = sin 2θEΦΘ ∂θ ∂θ ∂ϕ 2 For sake of simplicity, we have factored the term 2 h – 2I into the energy. At the end of the calculation we Will multiply by this term to obtain the energy. Separation of variables The operators in variables θ and φ operate on functio Θ and Φ , respectively, so we can write 2 Θ ∂ Φ2 + Φsinθ ∂ sinθ ∂Θ = sin θEΦΘ ∂θ ∂θ ∂ϕ 2 When we divide by Y = ΘΦ, we obtain 2 ∂ 1 Φ + 1 sinθ ∂ sinθ ∂Θ – sin 2θE = 0 Φ ∂ϕ 2 Θ ∂θ ∂θ Now, these equations can be separated. Separation of variables We use a separation constant equal to m2 to write two equations. The θ and φ equations are sinθ ∂ sinθ ∂Θ Θ ∂θ ∂θ 2 1 ∂Φ Φ ∂φ 2 – sin θE = m 2 2 = – m2 We have already seen the solution to the φ equation from the example of rotation in two dimensions. The solution of θ equation gives Legendre polynomials Substitute x = cosθ and the equation becomes: 2 ∂ P m ∂P 1–x – 2x + E– P=0 2 2 ∂x 1–x ∂x 2 2 The solution requires that Ε=-(h2/2I)J(J+1) with J=0,1,2 Where J is the rotational quantum number. The azimuthal quantum number m is also called Jz. The magnitude of |Jz|<J. The solutions are Legendre polynomials P0(x)=1 P2(x)=1/2 (3x2 - 1) P1(x)=x P3(x)=1/2 (5x3 - 3x) The spherical harmonics as solutions to the rotational hamiltonian The spherical harmonics are the product of the solutions to the θ and φ equations. With norm-alization these solutions are Y (θ,φ) = NJMP (cos θ)e M J |M| J iMφ The M quantum number corresponds to Jz the z component of angular momentum. The norm-alization constant is NJM (J – |M|)! 2J + 1 = 2 (J + |M|)! 1/2 The form of the spherical harmonics Including normalization the spherical harmonics are Y00 = 1 4π 0 3 cosθ Y1 = 4π ±1 Y1 = 0 Y2 = ±1 2 Y = 3 sinθe ±iφ 2 Y2 = 8π 5 3cos 2θ – 1 16π 15 sinθcosθe ±iφ 8π 15 sin 2θe ±2iφ 32π The form commonly used to represent p and d orbitals are linear combinations of these functions Euler relation Linear combinations are formed using the Euler relatio e ±iφ = cosθ ± isinθ iφ –iφ sinθ = e – e 2i iφ –iφ + e e cosθ = 2 Projection along the z-axis is usually taken using z = rcosθ. Projection in the x,y plane is taken using x = rsinθcosφ and y = rsinθsinφ The 3-D rotational hamiltonian • There are two quantum numbers J is the total angular momentum quantum number M is the z-component of the angular momentum • The spherical harmonics called YJM are functions whose probability |YJM|2 has the well known shape of the s, p and d orbitals etc. • J = 0 is s , M = 0 • J = 1 is p , M = -1, 0 , 1 • J = 2 is d , M = -2 , -1, 0 , 1, 2 Space quantization in 3D • Solutions of the rotational Schrödinger equation have z M = +2 M = +1 M=0 M = -1 M = -2 J=2 energies E = h2 J(J +1)/2I • Specification of the azimuthal quantum number mz implies that the angular momentum about the z-axis is Jz = hmz. • This implies a fixed orientation between the total angular momentum and the z component. • The x and y components cannot be known due to the Uncertainty principle. Spherical harmonic for P0(cosθ) • Plot in polar coordinates represents |Y00|2 where Y00=(1/4π)1/2 . • Solution corresponds to rotational quantum numbers J = 0, • M or Jz = 0. • Polynomial is valid for n≥1 quantum numbers of hydrogen wavefunctions Spherical harmonic for P1(cosθ) • Plot in polar coordinates represents |Y11|2 where Y11=(1/2)(3/2π)1/2 sinθeiφ. • Solution corresponds to rotational quantum numbers J = 1, Jz = ±1. • Polynomial is valid for n≥2 quantum numbers of hydrogen wavefunctions Spherical harmonic for P1(cosθ) • Plot in polar coordinates represents |Y10|2 where Y10=(1/2)(3/π)1/2 cosθ with normalization. • Solution corresponds to rotational quantum numbers J = 1, Jz = 0. • Polynomial is valid for n≥2 quantum numbers of hydrogen wavefunctions. Spherical harmonic for P2(cosθ) • Plot in polar coordinates of |Y22|2 where Y22=1/4(15/2π)1/2cos2θe2iφ • Solution corresponds to rotational quantum numbers J = 2, Jz = ± 2. • Polynomial is valid for n≥3 quantum numbers of hydrogen wavefunctions Spherical harmonic for P2(cosθ) • Plot in polar coordinates of |Y21|2 where Y21=(15/8π)1/2sinθcosθeiφ • Solution corresponds to rotational quantum numbers J = 2, Jz = ± 1. • Polynomial is valid for n≥3 quantum numbers of hydrogen wavefunctions Spherical harmonic for P2(cosθ) • Plot in polar coordinates of |Y20|2 where Y20=1/4(5/π)1/2(3cos2θ-1) • Solution corresponds to rotational quantum numbers J = 1, Jz = 0. • Polynomial is valid for n≥3 quantum numbers of hydrogen wavefunctions Rotational Wavefunctions J=0 J=1 J=2 These are the spherical harmonics YJM, which are solutions of the angular Schrodinger equation. The degeneracy of the solutions • The solutions form a set of 2J + 1 functions at each energy (the energies are E = h2 J(J +1)/2I. • A set of levels that are equal in energy is called a degenerate set. J=3 J=2 J=1 J=0 Rotational Transitions • Electromagnetic radiation can interact with a molecule to change the rotational state. • Typical rotational transitions occur in the microwave region of the electromagnetic spectrum. • There is a selection rule that states that the quantum number can change only by + or - 1 for an allowed rotational transition (ΔJ = ±1). J=2 J=1 J=0 Orthogonality of wavefunctions • The rotational wavefunctions can be represented as the product of sines and cosines. • Ignoring normalization we have: • s 1 • p cosθ sinθcosφ sinθsinφ • d 1/2(3cos2θ - 1), cos2θcos2φ , cos2θsin2φ , cosθsinθcosφ , cosθsinθsinφ • The differential angular element is sinθdθdφ/4π over • the limits θ = 0 to π and φ = 0 to 2π. • The angular wavefunctions are orthogonal. Orthogonality of wavefunctions • For the theta integrals we can use the substitution • x = cosθ and dx = sinθdθ • For example, for s and p-type rotational wave functions we have π <s|p>∝ –1 cosθ sinθ dθ = 0 1 2 x x dx = 2 –1 1 = 1 – 1 =0 2 2 Question Which of the following statements is true: A. The number of z-projection of the quantum numbers is 2J+1. B. The spacing between rotational energy levels increases as 2(J+1). C. Rotational energy levels have a degeneracy of 2J+1. D. All of the above. Question Which of the following statements is true: A. The number of z-projection of the quantum numbers is 2J+1. B. The spacing between rotational energy levels increases as 2(J+1). C. Rotational energy levels have a degeneracy of 2J+1. D. All of the above. ΔE ~ (J +2)(J + 1) – J(J + 1) = 2(J + 1) Question The fact that rotational wave functions are orthogonal means that A. They have no overlap B. They are normalized C. They are linear functions D. None of the above Question The fact that rotational wave functions are orthogonal means that A. They have no overlap B. They are normalized C. They are linear functions D. None of the above The moment of inertia The kinetic energy of a rotating body is 1/2Iω2. The moment of inertia is given by: ∞ I= Σ mr i=1 2 i i The rigid rotor approximation assumes that molecules do not distort under rotation. The types or rotor are (with moments Ia , Ib , Ic) - Spherical: Three equal moments (CH4, SF6) (Note: No dipole moment) - Symmetric: Two equal moments (NH3, CH3CN) - Linear: One moment (CO2, HCl, HCN) (Note: Dipole moment depends on asymmetry) - Asymmetric: Three unequal moments (H2O) The rotational partition function The degeneracy of rotational levels is J(J+1). The energies are given by ε = hcBJ(J+1) where J is the rotational quantum number and B is the rotational constant. ∞ qr = Σ J=0 (2J + 1)e – βhcBJ(J + 1) A large number of rotational levels populated since the rotational constant is of the order of 10 cm -1 for many molecules and kT > 10 cm-1 for temperatures higher than about 15 K. The high temperature form of the rotational partition function The partition function can be expressed as an integral at high temperature. ∞ qr = (2J + 1)e – βhcBJ(J + 1)dJ 0 It turns out that the integral can be solved analytically by making the substitution u = J(J+1). u = J(J + 1), du = (2J + 1)dJ The rotational partition function is an exponential integral Making the substitution u = J(J+1) the integral reduces to an easily soluble exponential integral. ∞ qr = e 0 – βhcBu 1 du = βhcB The rotational constant B is: B= h where I is the moment of inertia 4πcI